Содержание
- 2. Секущей плоскостью тетраэдра (параллелепипеда) называется любая плоскость, по обе стороны от которой имеются точки данного многогранника.
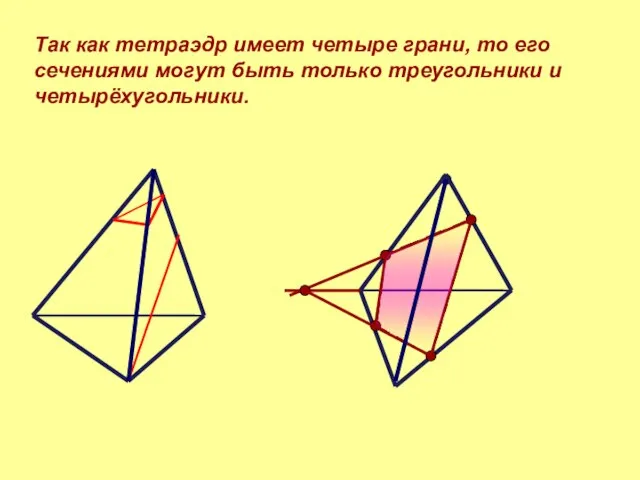
- 3. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
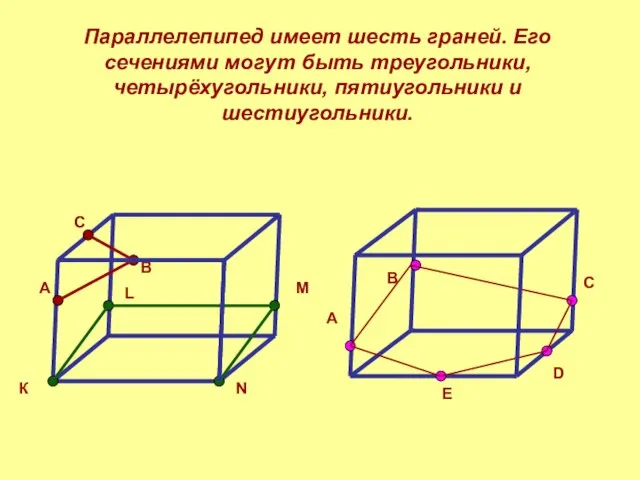
- 4. Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники. А В С
- 5. Алгоритм построения сечений многогранников: а) определить грани, с которыми секущая плоскость имеет две общие точки, и
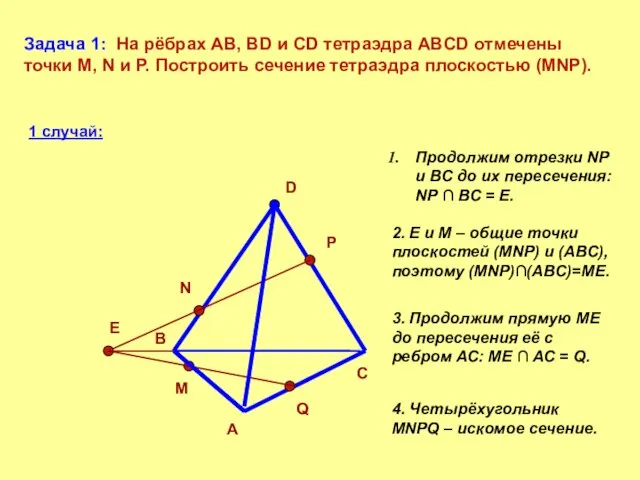
- 6. Задача 1: На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки M, N и P.
- 7. 2 случай: прямые NP ll BC. A B C D N P M Q Если NP
- 8. Задача 2: Точка М лежит на боковой грани АDВ тетраэдра DАВС. Построить сечение тетраэдра плоскостью, проходящей
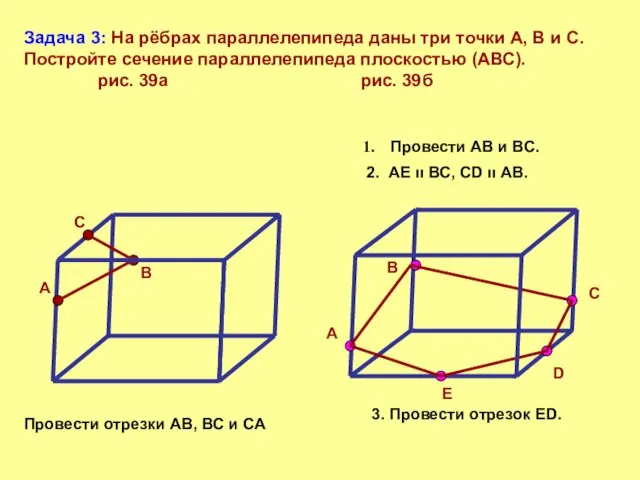
- 9. Задача 3: На рёбрах параллелепипеда даны три точки А, В и С. Постройте сечение параллелепипеда плоскостью
- 10. Задача 3: На рёбрах параллелепипеда даны три точки А, В и С. Постройте сечение параллелепипеда плоскостью
- 11. Решение задач на построение сечений
- 15. D А В С Е К М Задача: На рёбрах AD и DC тетраэдра DABC взяты
- 16. А В С D А1 В1 С1 D1 № 81: М є ВВ1, Nє СС1. Построить
- 17. А В С D А1 В1 С1 D1 № 82в: М є (АА1В1). Постройте сечение, проходящее
- 18. А В С D А1 В1 С1 D1 № 83: Постройте сечение, проходящее: а) через СС1
- 19. А В С D А1 В1 С1 D1 М К L N O 1. Построим KL
- 20. В А D С В1 А1 D1 С1 № 84: Построить сечение проходящее через точки B1,
- 21. А D С В А1 D1 С1 В1 № 85: Построить сечение (BKL), где К и
- 22. А D С В А1 D1 С1 В1 № 86: Построить сечение проходящее через диагональ АС
- 23. D A B C D1 A1 B1 C1 № 87а: Постройте сечение плоскостью (MNK), где М
- 24. А В С D А1 В1 С1 D1 № 87б: Постройте сечение плоскостью (MNK), где М
- 26. Скачать презентацию



















 Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса
Математическая шкатулка. Внеклассное мероприятие для учащихся 8 класса Многогранники
Многогранники Средняя линия треугольника. Задачи
Средняя линия треугольника. Задачи Отображение множеств
Отображение множеств Шкала. Координатный луч
Шкала. Координатный луч Выборочное наблюдение
Выборочное наблюдение Занимательная математика
Занимательная математика Метрические соотношения в прямоугольном треугольнике
Метрические соотношения в прямоугольном треугольнике Комбинаторика 10 класс - презентация по математике_
Комбинаторика 10 класс - презентация по математике_ Начальные геометрические сведения
Начальные геометрические сведения Вычисления в MATLAB
Вычисления в MATLAB Элементы статистики. (8 класс)
Элементы статистики. (8 класс) Решение уравнений высших степеней с помощью теоремы Безу
Решение уравнений высших степеней с помощью теоремы Безу Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Презентация урока математики 4 класс Учителя начальных классов МОУ лицей Павловой Светланы Аркадьевны
Презентация урока математики 4 класс Учителя начальных классов МОУ лицей Павловой Светланы Аркадьевны  Умножение и деление натуральных чисел Математика 5 класс БИКЛАМБЕТОВА РАМЗИЯ АНВАРОВНА МКОУ «ОСЫПНОБУГОРСКАЯ СОШ»
Умножение и деление натуральных чисел Математика 5 класс БИКЛАМБЕТОВА РАМЗИЯ АНВАРОВНА МКОУ «ОСЫПНОБУГОРСКАЯ СОШ»  Конкурс «Удивительные дети» (10 класс)
Конкурс «Удивительные дети» (10 класс) Математика в в профессии
Математика в в профессии Основные законы теории вероятности
Основные законы теории вероятности Системы счисления
Системы счисления Неопределенный интеграл. (Лекция 1)
Неопределенный интеграл. (Лекция 1) Целые выражения
Целые выражения  Прямоугольник. Квадрат
Прямоугольник. Квадрат Угол. Виды углов
Угол. Виды углов 1, 618 - число Фи!
1, 618 - число Фи! Производная функции
Производная функции Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Теорема синусов. Теорема косинусов
Теорема синусов. Теорема косинусов