Содержание
- 2. Графики основных элементарных функций Основными элементарными функциями называются функции: постоянная, степенная, показательная, логарифмическая, тригонометрические и обратные
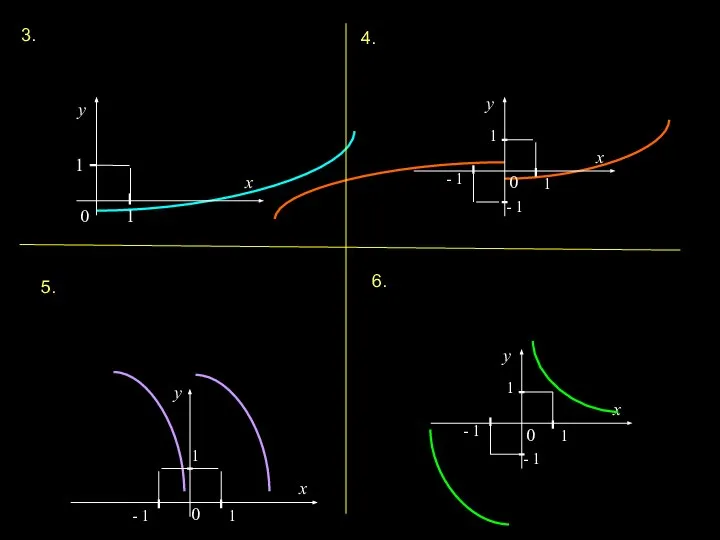
- 3. . 3. 4. 5. 6.
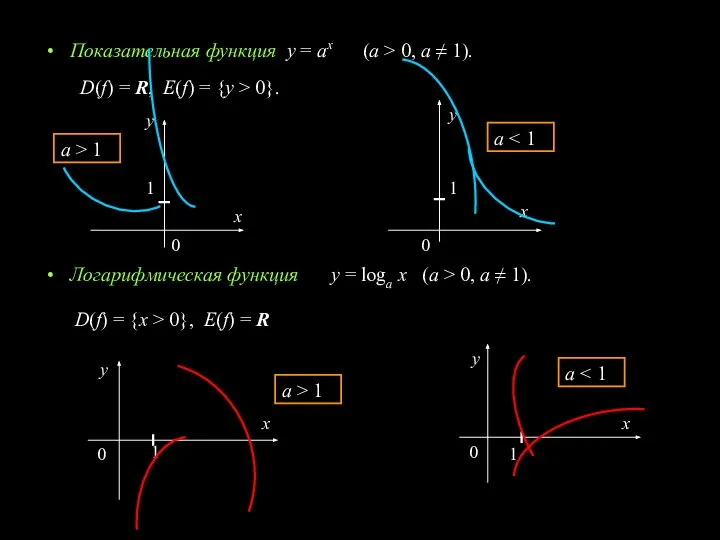
- 4. Показательная функция y = ax (a > 0, a ≠ 1). Логарифмическая функция y = loga
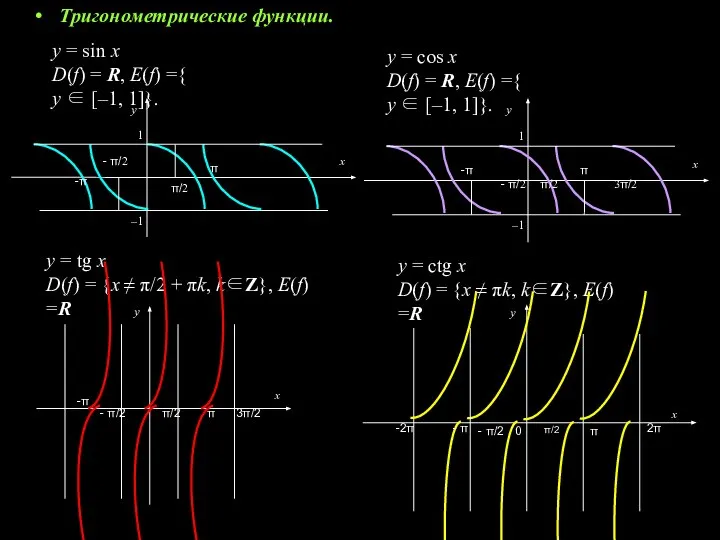
- 5. Тригонометрические функции. y = sin x D(f) = R, Е(f) ={ y ∈ [–1, 1]}. y
- 6. Обратные тригонометрические функции. y = arcsin x D(f) = [–1, 1], Е(f) = [–π/2, π/2]. y
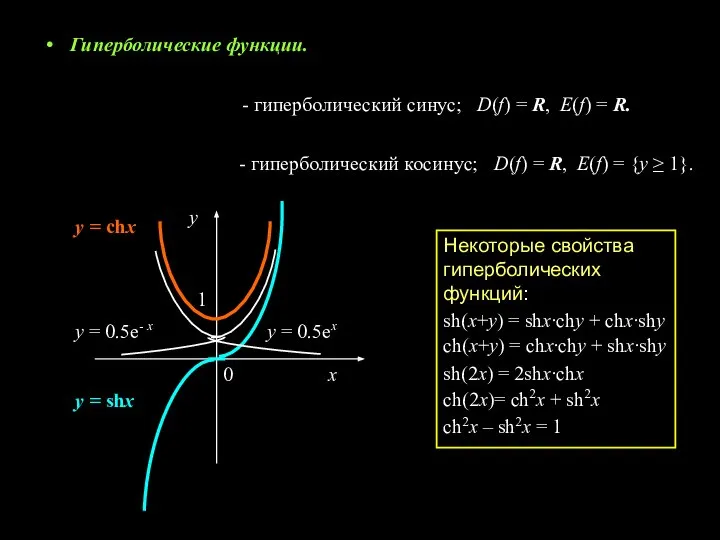
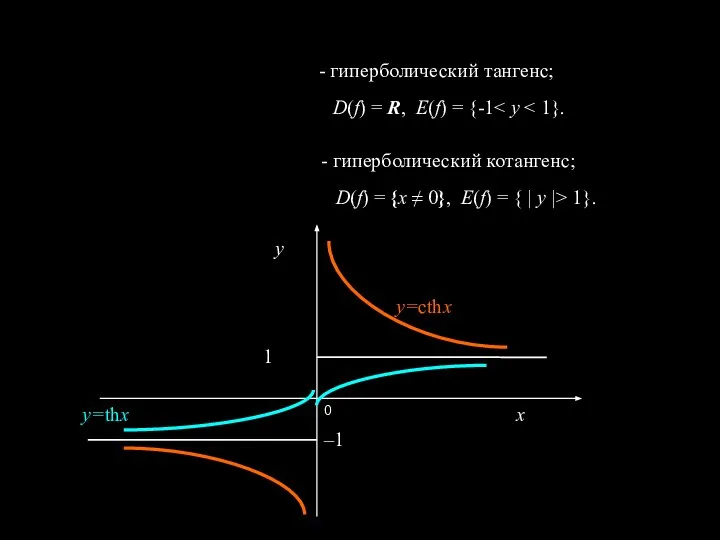
- 7. Гиперболические функции. Некоторые свойства гиперболических функций: sh(x+у) = shx·сhу + сhx·shу сh(x+у) = сhx·сhу + shx·shу
- 8. - гиперболический тангенс; - гиперболический котангенс; D(f) = R, Е(f) = {-1 D(f) = {x ≠
- 9. Понятие числовой последовательности. Если каждому числу n∈N поставлено в соответствие определённое число хn ∈ R, то
- 10. Примеры. 1, 1, 1, … ⇔ хn=1, ∀n∈N ; –1, 1, –1, 1, … ⇔ хn=
- 11. Арифметическая и и геометрическая прогрессии
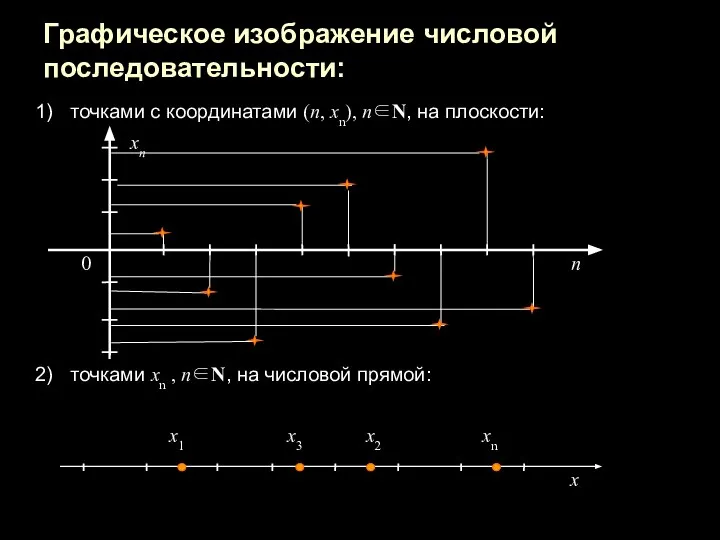
- 12. Графическое изображение числовой последовательности: точками с координатами (n, хn), n∈N, на плоскости: точками хn , n∈N,
- 13. Определение предела последовательности Число a ∈ R называется пределом (числовой) последовательности {хn}, если для любого числа
- 14. Геометрический вариант определения предела. Неравенство ⎜хn – a⎜ a – ε Другими словами, для любого числа
- 15. Единственность предела ТЕОРЕМА. Числовая последовательность может иметь лишь один предел. Доказательство. Предположим, что {хn} имеет два
- 16. Ограниченность сходящейся ЧП. ЧП называется ограниченной, если множество ее значений ограничено сверху и снизу, т.е. ∃
- 17. ТЕОРЕМА. Если числовая последовательность имеет предел, то она ограничена. Доказательство. Пусть Возьмем ε = 1. Согласно
- 18. Л ЛЕММА. Если хn→ а при n → ∞, а ≠ 0 и хn ≠ 0
- 20. Скачать презентацию

![Обратные тригонометрические функции. y = arcsin x D(f) = [–1, 1],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1296479/slide-5.jpg)









 Аттестационная работа. Разработка по выполнению исследовательской работы с учащимися «Быт села Каразей. От печи до камина»
Аттестационная работа. Разработка по выполнению исследовательской работы с учащимися «Быт села Каразей. От печи до камина»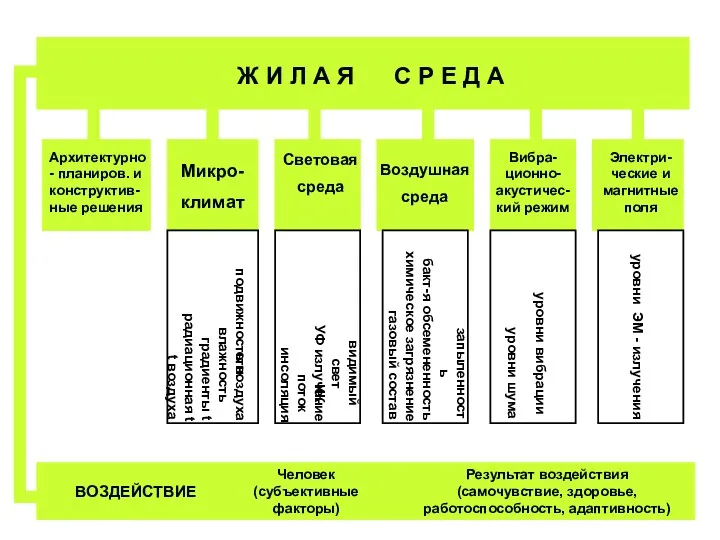 Жилая среда
Жилая среда Пять координационных механизмов по Г. Минцбергу
Пять координационных механизмов по Г. Минцбергу смекай, считай, отгадывай презентация_
смекай, считай, отгадывай презентация_ Понятие и сущность организации
Понятие и сущность организации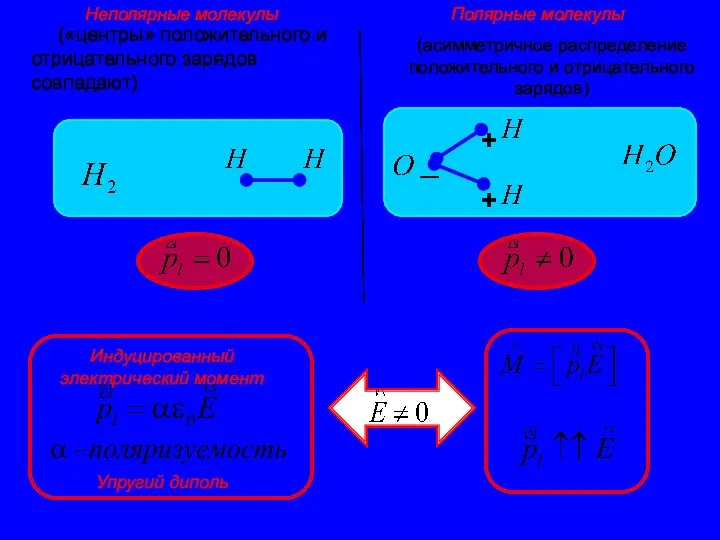 Поляризация диэлектриков
Поляризация диэлектриков  ТСТ Trust Capital Trade – формула несокрушимой торговли
ТСТ Trust Capital Trade – формула несокрушимой торговли Мультиметр
Мультиметр РАЗВИТИЕ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ МЛАДШИХ ШКОЛЬНИКОВ Выполнила: Кучмасова С.А. учитель начальных классов
РАЗВИТИЕ ТВОРЧЕСКИХ СПОСОБНОСТЕЙ МЛАДШИХ ШКОЛЬНИКОВ Выполнила: Кучмасова С.А. учитель начальных классов  Вода - растворитель. Значение воды - презентация для начальной школы
Вода - растворитель. Значение воды - презентация для начальной школы Арабский халифат. (6 класс)
Арабский халифат. (6 класс) Php Oպերատորները
Php Oպերատորները Логическое выражение
Логическое выражение Дисгармоничное развитие
Дисгармоничное развитие Стандартизация, сертификация и товароведение. Про специальность
Стандартизация, сертификация и товароведение. Про специальность Стратегический менеджмент. Этапы стратегического управления
Стратегический менеджмент. Этапы стратегического управления Почему в лесу нужно соблюдать тишину? Автор: Кульчицкая И.Н. Учитель начальных классов.
Почему в лесу нужно соблюдать тишину? Автор: Кульчицкая И.Н. Учитель начальных классов. Материалы к педсовету Работа по теме самообразования учителя русского языка и литературы Паньшиной И.С.
Материалы к педсовету Работа по теме самообразования учителя русского языка и литературы Паньшиной И.С. Класс МЛЕКОПИТАЮЩИЕ MAMMALIA
Класс МЛЕКОПИТАЮЩИЕ MAMMALIA Психолог начальной школы ГОУ СОШ № 581 Родителям учащихся 9.12.2010
Психолог начальной школы ГОУ СОШ № 581 Родителям учащихся 9.12.2010 Увидеть Россию
Увидеть Россию Архыз - 2018. Карачаево-Черкесия
Архыз - 2018. Карачаево-Черкесия Определение чувствительности к антибиотикам. Культивирование анаэробов. Диагностика с помощью бактериофагов
Определение чувствительности к антибиотикам. Культивирование анаэробов. Диагностика с помощью бактериофагов  Виды дисперсий
Виды дисперсий  Чувашская национально-культурная автономия г. Челябинска. Молодёжная организация «Креативная Команда «Кадэрне»
Чувашская национально-культурная автономия г. Челябинска. Молодёжная организация «Креативная Команда «Кадэрне» Теплопроводность бетона
Теплопроводность бетона Что такое функция ? - презентация по Алгебре
Что такое функция ? - презентация по Алгебре Интернационализация, транснационализация, глобализация МЭ
Интернационализация, транснационализация, глобализация МЭ