Interconnect delay. (Chapter 7)

Chapter 7 Interconnect Delay

7.1 Elmore Delay
7.2 High-order model and moment matching
7.3

Basic Circuit Analysis Techniques

Output response
Basic waveforms
Step input
Pulse input
Impulse Input
Use simple input

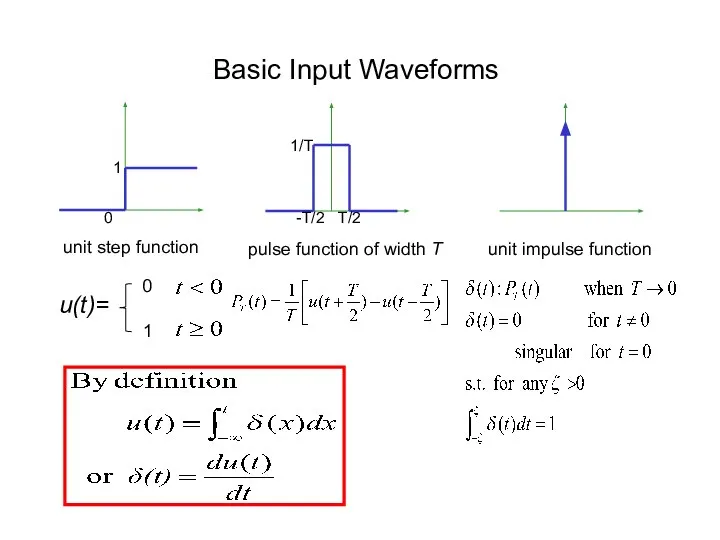
unit step function

u(t)=

0

1

1

pulse function of width T

0

1/T

-T/2

T/2

unit impulse function

Basic Input Waveforms

Definitions:
(unit) step input u(t) (unit) step response g(t)
(unit) impulse input δ(t) (unit)

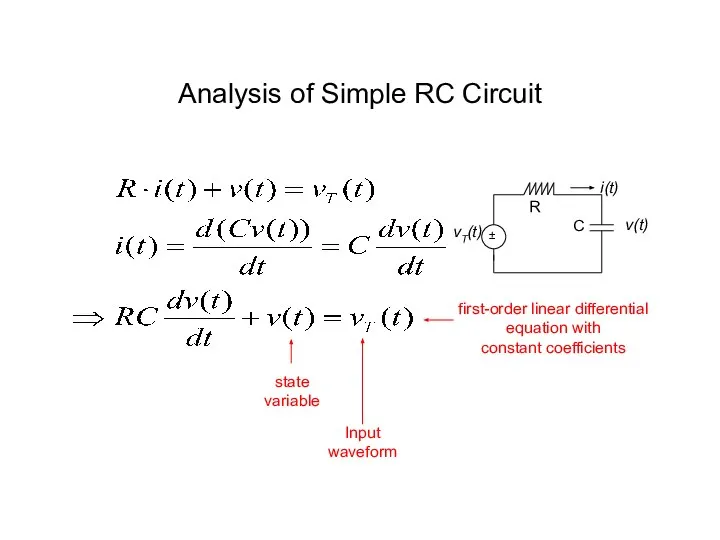
Analysis of Simple RC Circuit

first-order linear differential
equation with
constant coefficients

state variable

Input
waveform

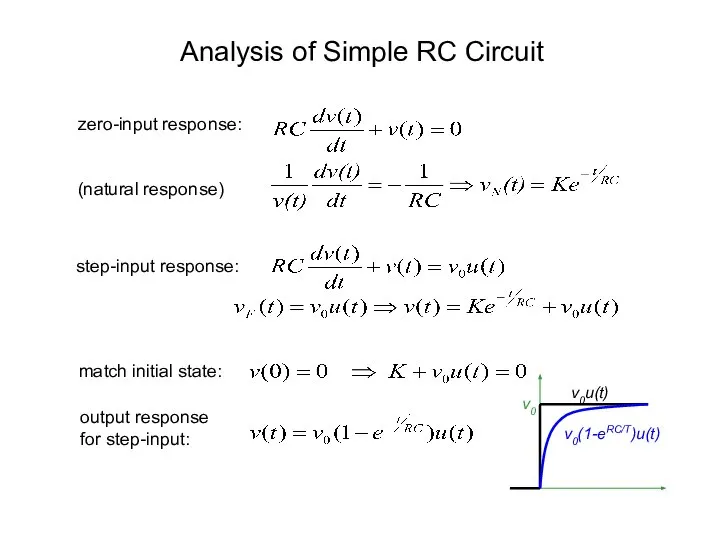
Analysis of Simple RC Circuit

zero-input response:

(natural response)

step-input response:

match initial state:

output response
for

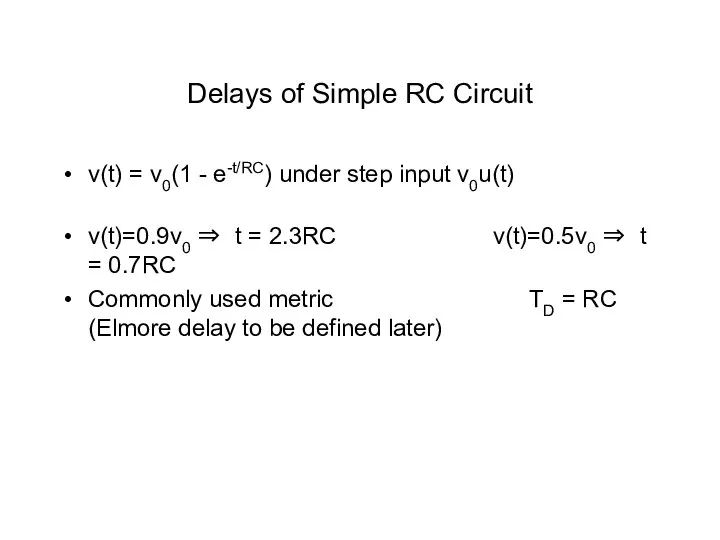
Delays of Simple RC Circuit

v(t) = v0(1 - e-t/RC) under step

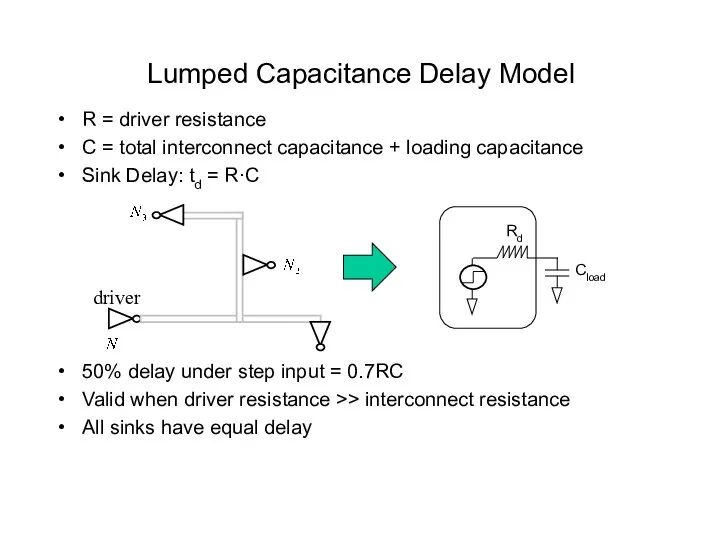
Lumped Capacitance Delay Model

R = driver resistance
C = total interconnect capacitance

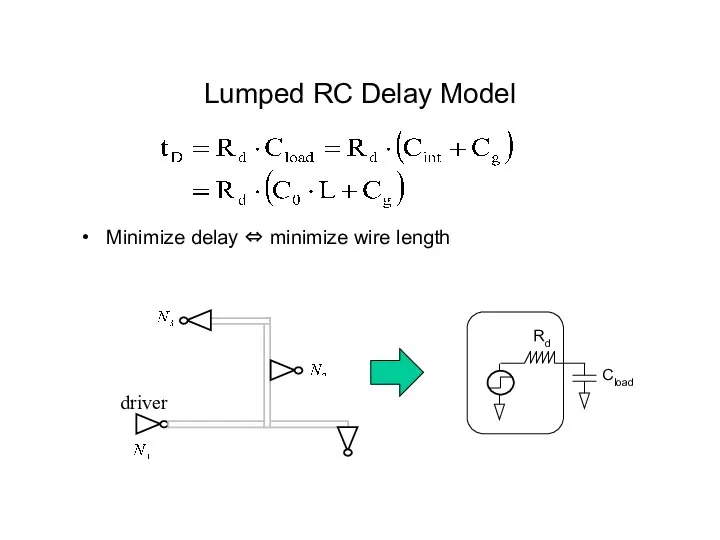
driver

Lumped RC Delay Model
Minimize delay ⇔ minimize wire length

Rd

Cload

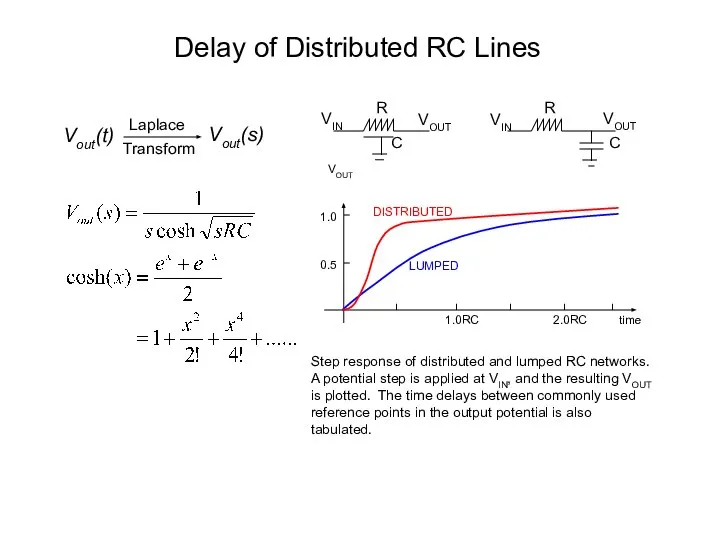
Delay of Distributed RC Lines

Vout(t)

Vout(s)

Laplace

Transform

R

VIN

VOUT

C

VOUT

VIN

R

C

0.5

1.0

VOUT

DISTRIBUTED

LUMPED

1.0RC

2.0RC

time

Step response of distributed and lumped RC

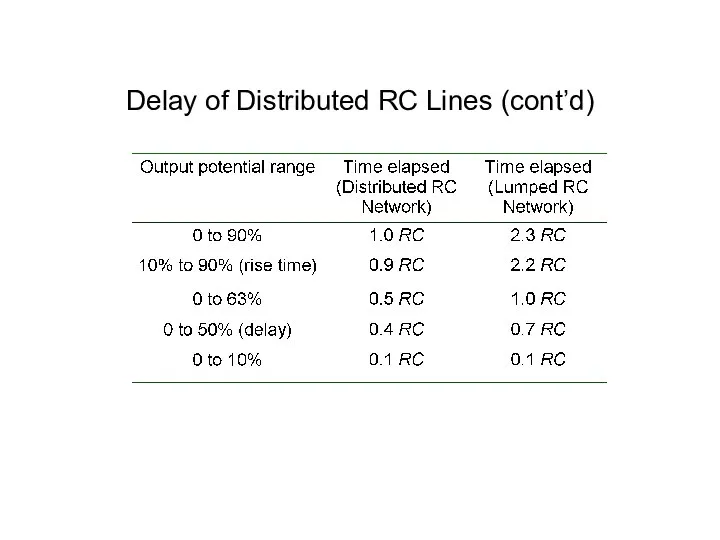
Delay of Distributed RC Lines (cont’d)

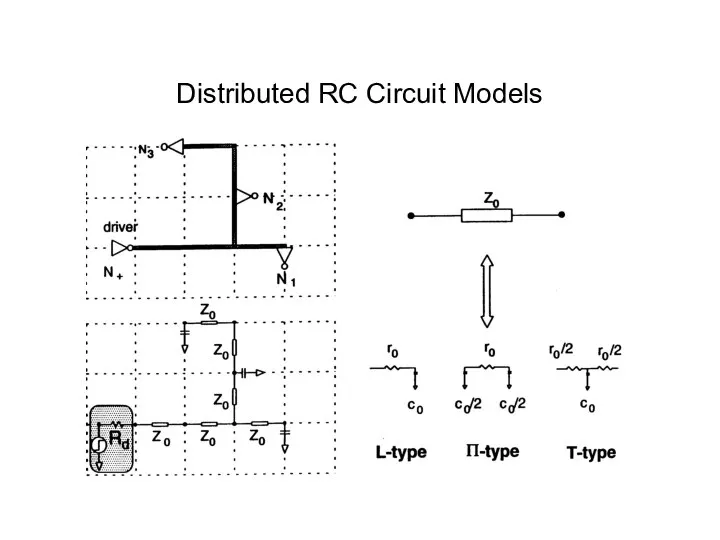
Distributed Interconnect Models

Distributed RC circuit model
L,T or Π circuits
Distributed RCL circuit

Distributed RC Circuit Models

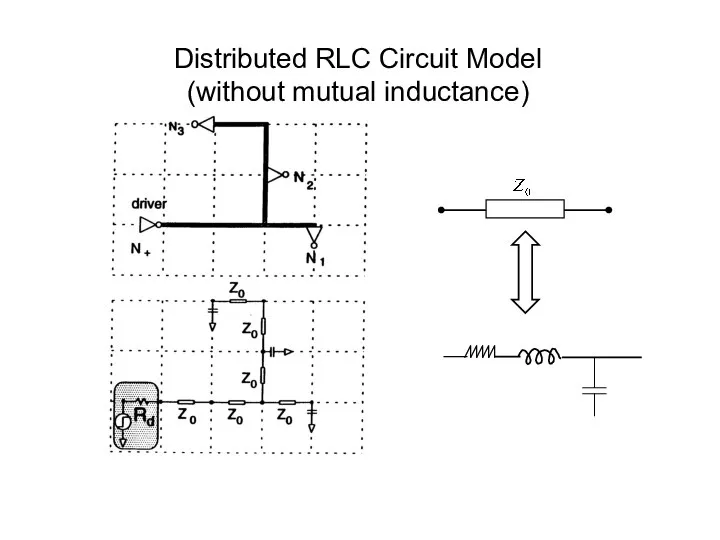
Distributed RLC Circuit Model (without mutual inductance)

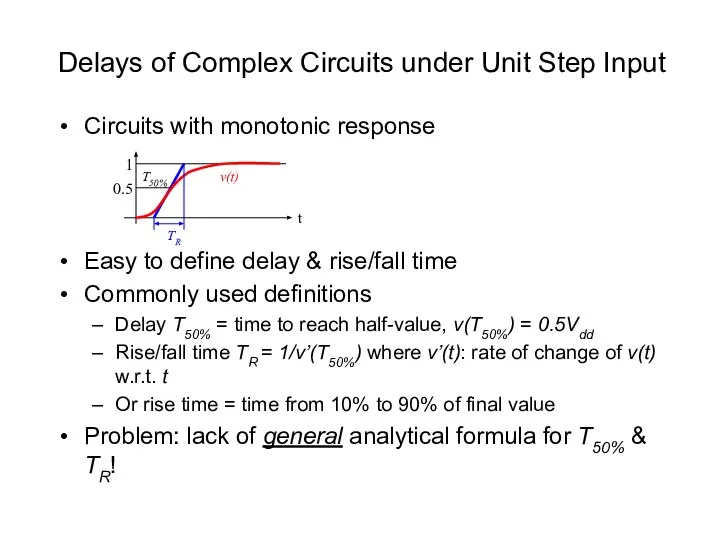
Delays of Complex Circuits under Unit Step Input

Circuits with monotonic response
Easy

Delays of Complex Circuits under Unit Step Input (cont’d)

Circuits with non-monotonic

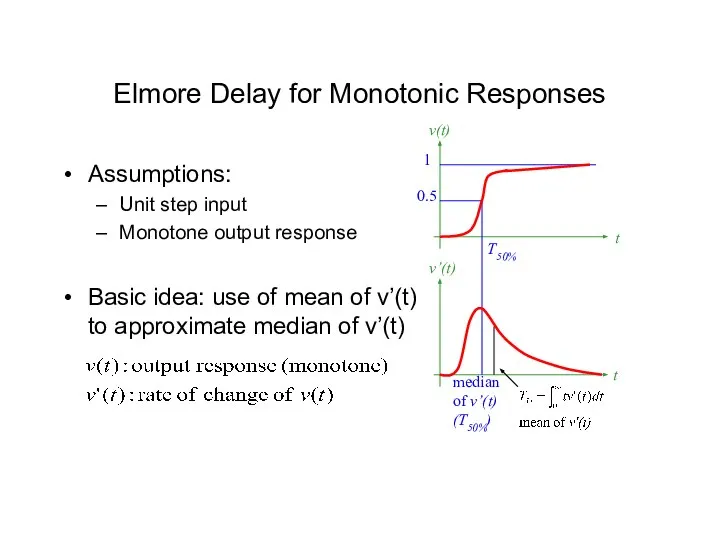
0.5

1

T50%

v(t)

t

t

v’(t)

median
of v’(t)
(T50%)

Elmore Delay for Monotonic Responses

Assumptions:
Unit step input
Monotone output response
Basic

T50%: median of v’(t), since
Elmore delay TD = mean of v’(t)

Elmore

Why Elmore Delay?

Elmore delay is easier to compute analytically in most

Elmore Delay for RC Trees

Definition
h(t) = impulse response
TD = mean of

Elmore Delay of a RC Tree [Rubinstein-Penfield-Horowitz, T-CAD’83]

Lemma:

Proof:

Apply impulse func. at t=0:

imin

i

current

Elmore Delay in a RC Tree (cont’d)

input

i

k

j

Si

path resistance Rii

Rjk

Theorem :

Proof

Elmore Delay in a RC Tree (cont’d)

We shall show later on

Some Definitions For Signal Bound Computation

Signal Bounds in RC Trees

Theorem

Delay Bounds in RC Trees

Computation of Elmore Delay & Delay Bounds in RC Trees

Let C(Tk)

Comments on Elmore Delay Model

Advantages
Simple closed-form expression
Useful for interconnect optimization
Upper bound

Comments on Elmore Delay Model

Disadvantages
Low accuracy, especially poor for slope computation
Inherently

Chapter 7.2 Higher-order Delay Model

Time Moments of Impulse Response h(t)

Definition of moments

i-th moment

Note that m1

Pade Approximation

H(s) can be modeled by Pade approximation of type

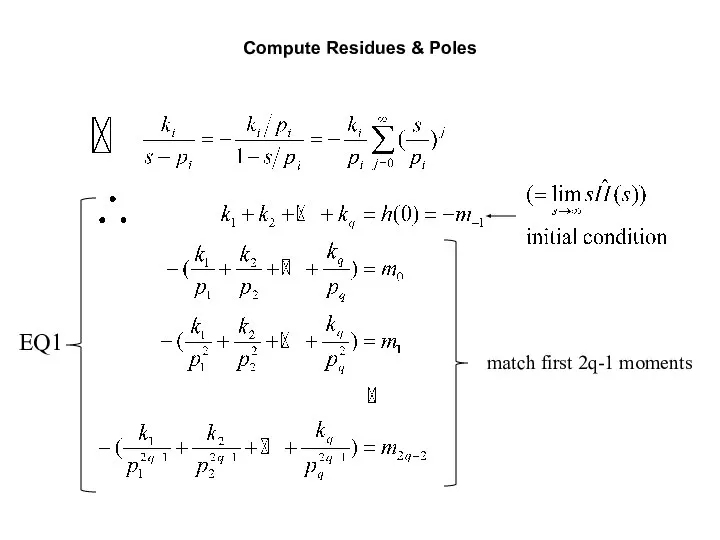
General Moment Matching Technique

Basic idea: match the moments m-(2q-r), …, m-1,

Compute Residues & Poles

match first 2q-1 moments

EQ1

Basic Steps for Moment Matching

Step 1: Compute 2q moments m-1, m0,

Components of Moment Matching Model

Moment computation
Iterative DC analysis on transformed equivalent

Chapter 7 Interconnect Delay

7.1 Elmore Delay
7.2 High-order model and moment matching
7.3

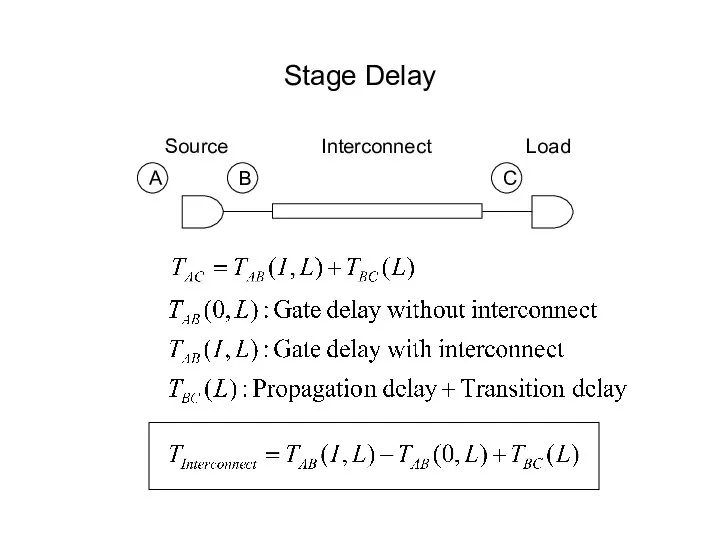
Stage Delay

A

B

C

Source

Interconnect

Load

Modeling of Capacitive Load

First-order approximation: the driver sees the total capacitance

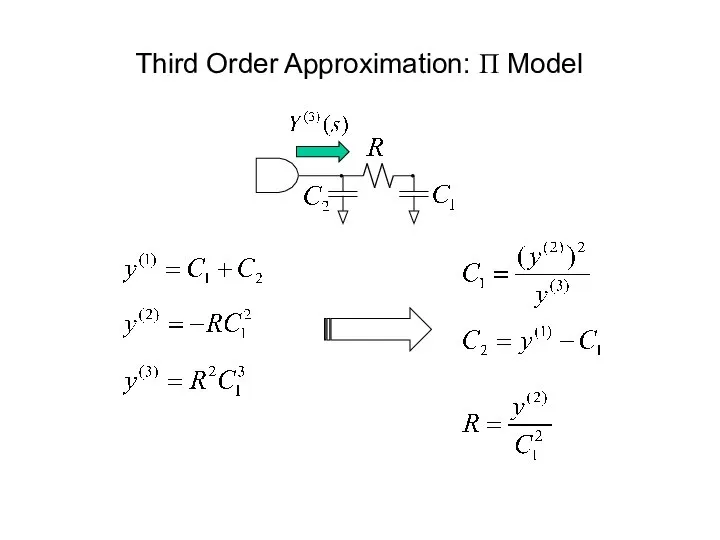
Π-Model [O’Brian-Savarino, ICCAD’89]

Moment matching again!
Consider the first three moments of driving point

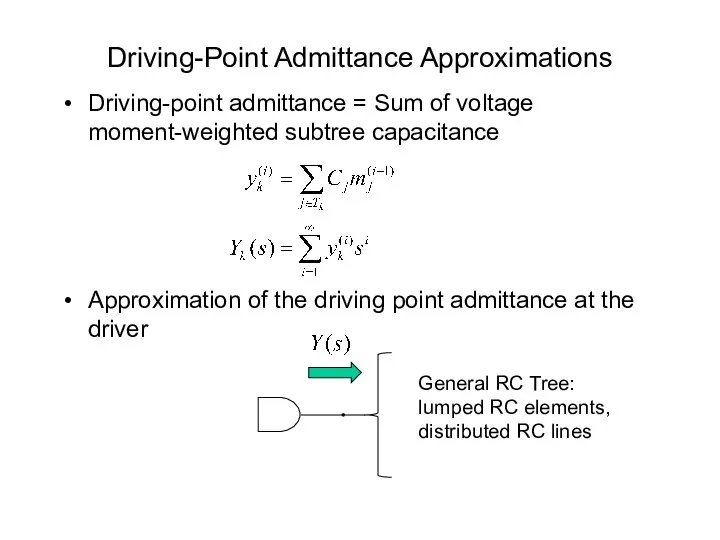
Driving-Point Admittance Approximations

Driving-point admittance = Sum of voltage moment-weighted subtree capacitance
Approximation

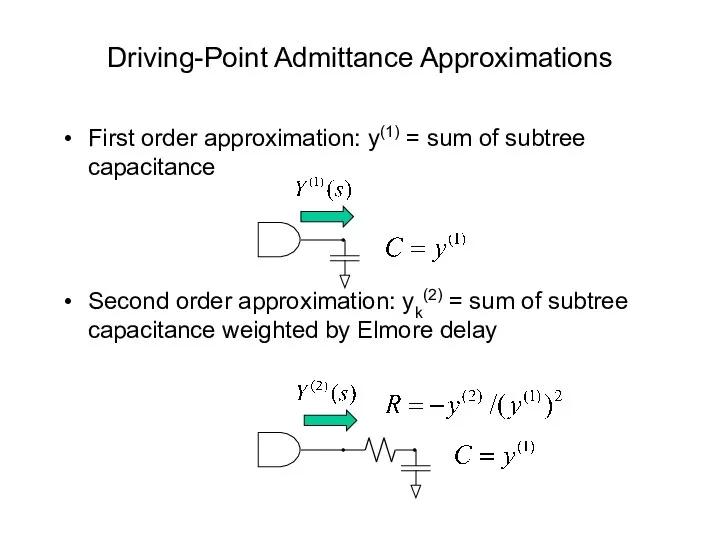
Driving-Point Admittance Approximations

First order approximation: y(1) = sum of subtree capacitance
Second

Third Order Approximation: Π Model

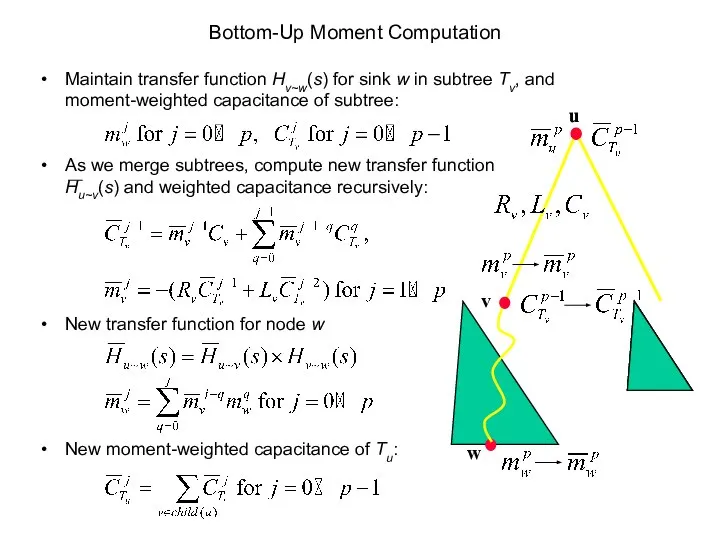
Current Moment Computation

Similar to the voltage moment computation
Iterative tree traversal:
O(n) run-time,

Bottom-Up Moment Computation

Maintain transfer function Hv~w(s) for sink w in subtree

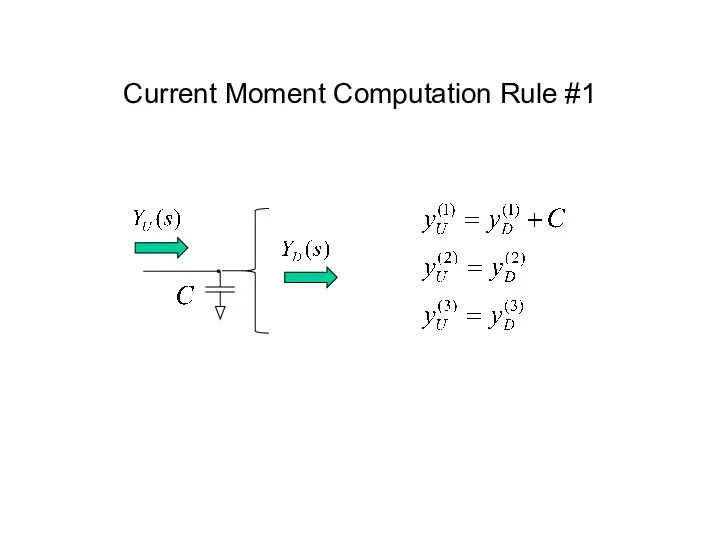
Current Moment Computation Rule #1

Current Moment Computation Rule #2

Current Moment Computation Rule #3

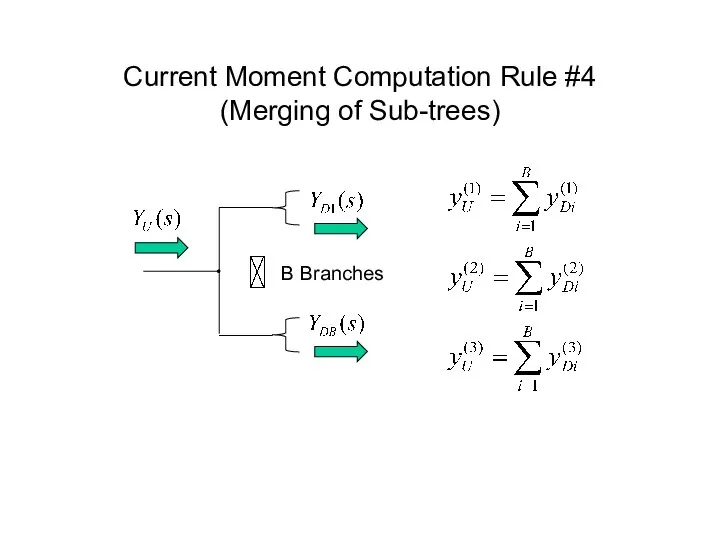
Current Moment Computation Rule #4 (Merging of Sub-trees)

B Branches

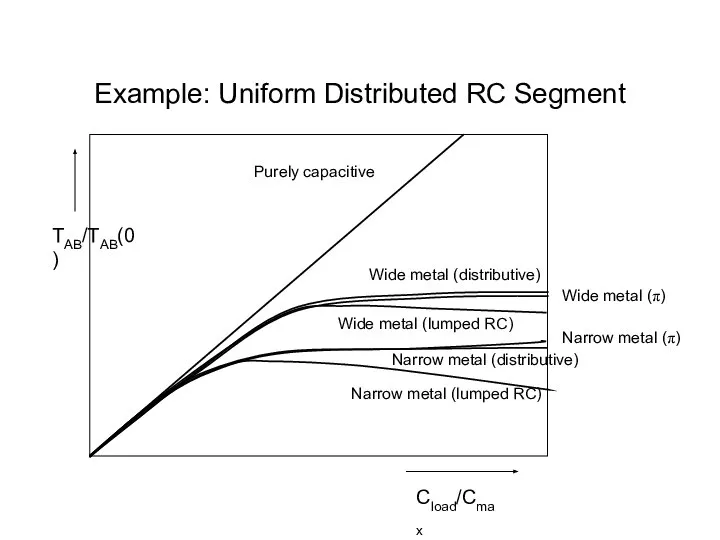
Example: Uniform Distributed RC Segment

Purely capacitive

Wide metal (distributive)

Narrow metal (distributive)

Narrow metal

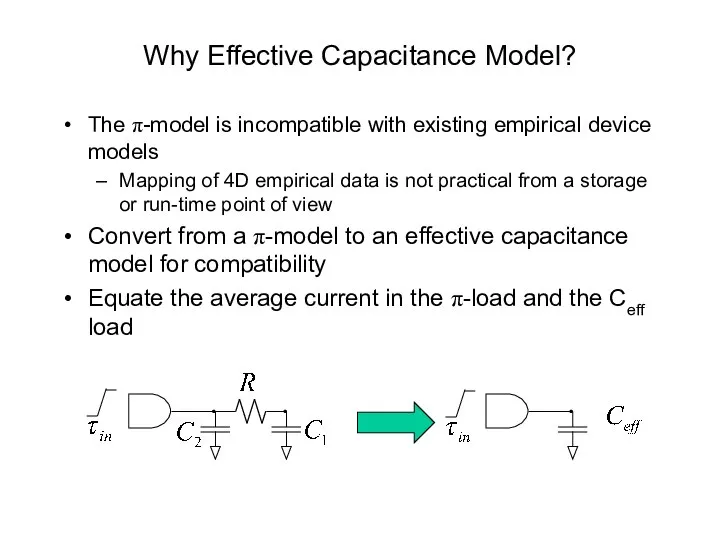
Why Effective Capacitance Model?

The π-model is incompatible with existing empirical device

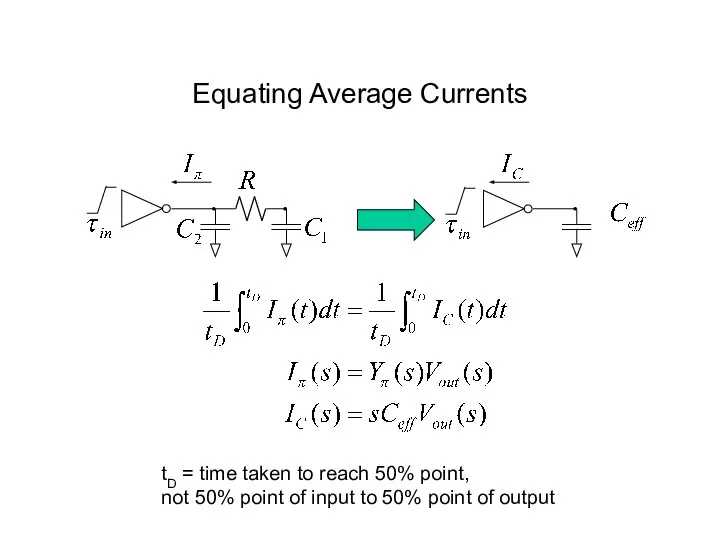
Equating Average Currents

tD = time taken to reach 50% point,
not

Waveform Approximation for Vout(t)

Quadratic from initial voltage (Vi = VDD for

Average Currents in Capacitors

Average current of C1 is not quite as

Average current for (0,tx) in C2
Average current for (tx,tD) in C2
Average

Computation of Effective Capacitance

Equating average currents
Problem: tD and tx are not