Вихревое течение. Теорема Томсона

Сентябрь 15, 2022

Главная
Физика
Вихревое течение. Теорема Томсона

Содержание

2. 1. Вихревое течение. Теорема Томсона. 2 разновидности линий тока Имеются источники и стоки (погашение течения на
3. Теорема Томсона: Циркуляция по «жидкому» контуру L, - т.е. по контуру, движущемуся вместе с жидкостью, при
4. По теореме Стокса: ≡ 0 2) Подынтегральная функция – полный дифференциал. Поэтому интеграл вдоль замкнутого контура
5. Течение жидкости, для которого rot v=0 называется потенциальным или безвихревым. Тогда ϕ− потенциал Вместо определения векторного
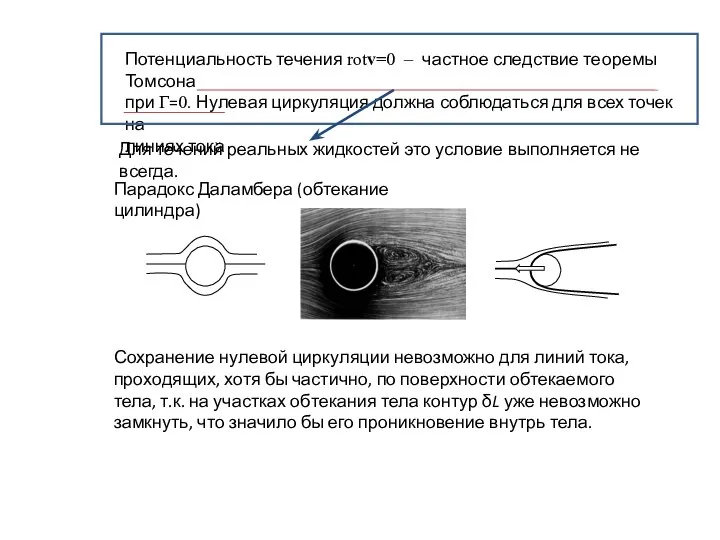
6. Потенциальность течения rotv=0 – частное следствие теоремы Томсона при Г=0. Нулевая циркуляция должна соблюдаться для всех
7. Примерная линия тока, вдоль которой нарушается условие нулевой циркуляции, показана на левом рис. штриховой кривой, состоящей
8. Вследствие вихреобразования симметричная картина течения и распределения давления относительно вертикальной оси пропадает Симметричная картина распределения давления
9. Общие требования плоские потенциальные стационарные течения идеальной несжимаемой жидкости: ρ=const, ∂ρ⁄∂t=0, ∂v/∂t=0 Уравнение неразрывности Уравнение Эйлера
10. Потенциал ϕ определяет скорость течения: v=∇ϕ и удовлетворяет уравнению Лапласа: Линии тока: в 2-х мерном случае
11. Комплексный потенциал W(z)=ϕ(x,y)+iψ(x,y) z=x+iy Отображение z⇒W(z) определяет функции ϕ и ψ, описывающие течение идеальной жидкости Требования
12. 1. Течение в угловой области
13. Картина линий тока в остро-уголовой области
14. Течение в области тупого угла
15. Течение в угловой области α>π/2
16. 2. Горизонтальное течение со стенкой Конформное преобразование
19. Обтекание цилиндра Конформное преобразование: R=1
21. Обтекание крыла (задача Жуковского) Конформное преобразование
24. Скачать презентацию

Слайд 2

1. Вихревое течение. Теорема Томсона.
2 разновидности линий тока
Имеются источники и

стоки
(погашение течения на ∞)
Линии тока не замкнуты

Имеется ось симметрии течения O
с неподвижными точками течения
Линии тока замкнуты
(источники, стоки отсутствуют)

Вихревое течение

Циркуляция

На круговой линии тока v||dl, |v|=const

Слайд 3

Теорема Томсона:
Циркуляция по «жидкому» контуру L, - т.е. по контуру, движущемуся
вместе

с жидкостью, при изоэнтропическом течении не меняется
со временем

r+dr

Вклад в циркуляцию
из-за изменения потока
со временем

Вклад в циркуляцию
из-за изменения
контура

т.к. из уравнения Эйлера

w – энтальпия (термодинамика):

Слайд 4

По теореме
Стокса:
≡ 0
2)
Подынтегральная функция – полный дифференциал.
Поэтому интеграл вдоль замкнутого

контура = 0

Равенства нулю обеих интегралов дает в итоге

что доказывает

теорему Томсона: Г=const

Слайд 5

Течение жидкости, для которого rot v=0 называется потенциальным или
безвихревым. Тогда
ϕ−

потенциал

Вместо определения векторного поля течения жидкости v=v(r,t) имеем
более простую задачу определения скалярного поля

Уточнение понятия потенциальности течения на основе теоремы Томсона

∙

δL – предельно малый контур вокруг произвольной точки на линии тока

δL

из-за стягивающегося к точке линии тока контура
величина rotv в пределах площади контура постоянна

2. Потенциальное течение идеальной жидкости.

Слайд 6

Потенциальность течения rotv=0 – частное следствие теоремы Томсона
при Г=0. Нулевая циркуляция

должна соблюдаться для всех точек на
линиях тока

Для течений реальных жидкостей это условие выполняется не всегда.

Парадокс Даламбера (обтекание цилиндра)

Сохранение нулевой циркуляции невозможно для линий тока, проходящих, хотя бы частично, по поверхности обтекаемого тела, т.к. на участках обтекания тела контур δL уже невозможно замкнуть, что значило бы его проникновение внутрь тела.

Слайд 7

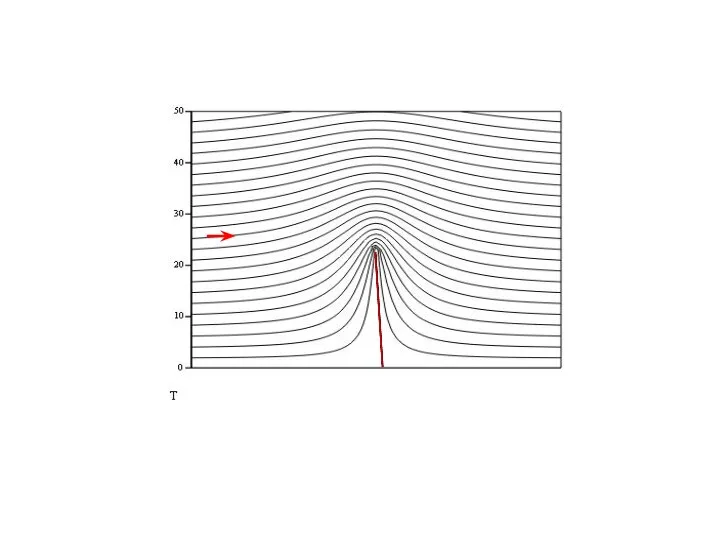
Примерная линия тока, вдоль которой нарушается условие нулевой циркуляции, показана на

левом рис. штриховой кривой, состоящей из двух горизонтальных участков априорно с нулевой циркуляцией и замкнутого контура обтекания с точками ненулевой циркуляции.

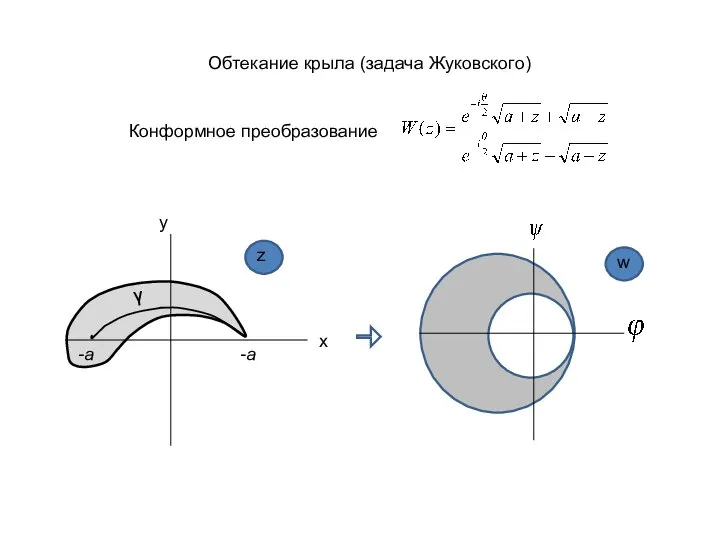
Другой пример - картина отрывного течения жидкости на правом рис. , когда за быстро движущимся телом образуется полость (каверна). Границы полости вместе с участком обтекания тела, показанные жирной линией, представляют линию тока в точках которой не выполняется сохранение нулевой циркуляции из-за невозможности продолжения контура.

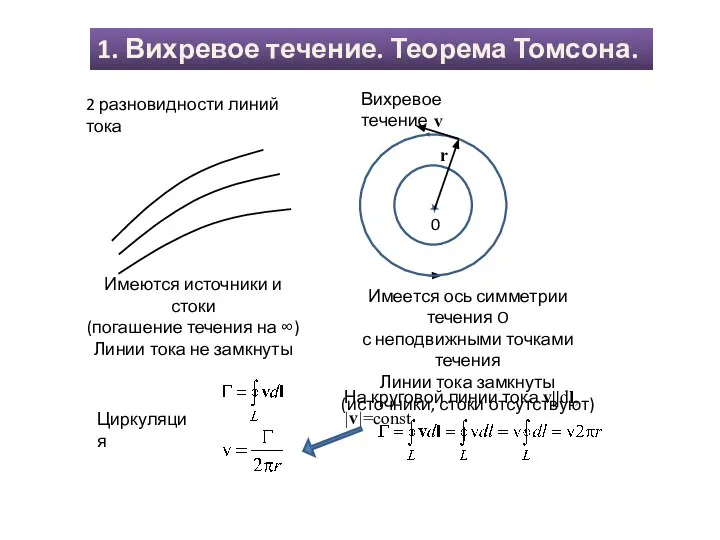
Существование наряду с "правильными" линиями тока (тонкие сплошные линии на левом и правом рисунках) линий тока с несохраняющейся циркуляцией (критические линии тока), выражает неоднозначность решений уравнений гидродинамики идеальной жидкости, вытекающей из недостаточной адекватности ее модели. Критические линии тока с участками ненулевой циркуляции оказываются источниками вихреобразования (средний рисунок).

Слайд 8

Вследствие вихреобразования симметричная картина течения
и распределения давления относительно вертикальной оси

пропадает

Симметричная картина распределения давления по верхней части цилиндра обуславливает отсутствие силы сопротивления, действующей на цилиндр (парадокс Даламбера)
Л. Эйлер объяснил происхождение парадокса неадекватностью модели идеальной жидкости, не учитывающей вязкость.

Слайд 9

Общие требования
плоские потенциальные стационарные течения идеальной несжимаемой жидкости: ρ=const, ∂ρ⁄∂t=0,

∂v/∂t=0
Уравнение
неразрывности
Уравнение Эйлера с учетом ∇P=0, ∂v/∂t=0 и равенства
=0
дополнительно к rot(v)=0
дает закон Бернулли

3. Метод комплексного потенциала

Слайд 10

Потенциал ϕ определяет скорость течения: v=∇ϕ и удовлетворяет уравнению Лапласа:
Линии

тока: в 2-х мерном случае ψ(x,y)=const

2) линии тока ортогональны линиям равного потенциала

условия аналитичности Коши-Римана

Слайд 11

Комплексный потенциал W(z)=ϕ(x,y)+iψ(x,y)
z=x+iy
Отображение z⇒W(z) определяет функции ϕ и ψ,
описывающие течение

идеальной жидкости

Требования к отображению z⇒W(z):
аналитичность функции W
сохранение углов (ортогональность)
однолистность

Слайд 12

1. Течение в угловой области

Слайд 13

Картина линий тока в остро-уголовой области

Слайд 14

Течение в области тупого угла

Слайд 15

Течение в угловой области α>π/2

Слайд 16

2. Горизонтальное течение со стенкой
Конформное преобразование

Слайд 17

Слайд 18

Слайд 19

Обтекание цилиндра
Конформное преобразование:
R=1

Слайд 20

Слайд 21

Обтекание крыла (задача Жуковского)
Конформное преобразование

Слайд 22

Вихревое течение. Теорема Томсона

Содержание

1. Вихревое течение. Теорема Томсона.2 разновидности линий тока Имеются источники и

Теорема Томсона:Циркуляция по «жидкому» контуру L, - т.е. по контуру, движущемусявместе

По теореме Стокса:≡ 02)Подынтегральная функция – полный дифференциал.Поэтому интеграл вдоль замкнутого

Течение жидкости, для которого rot v=0 называется потенциальным или безвихревым. Тогдаϕ−

Потенциальность течения rotv=0 – частное следствие теоремы Томсонапри Г=0. Нулевая циркуляция

Примерная линия тока, вдоль которой нарушается условие нулевой циркуляции, показана на

Вследствие вихреобразования симметричная картина течения и распределения давления относительно вертикальной оси

Общие требования плоские потенциальные стационарные течения идеальной несжимаемой жидкости: ρ=const, ∂ρ⁄∂t=0,

Потенциал ϕ определяет скорость течения: v=∇ϕ и удовлетворяет уравнению Лапласа: Линии

Комплексный потенциал W(z)=ϕ(x,y)+iψ(x,y) z=x+iyОтображение z⇒W(z) определяет функции ϕ и ψ,описывающие течение