Содержание
- 2. Точка A Прописные латинские буквы A, B, C, D, E, K, …
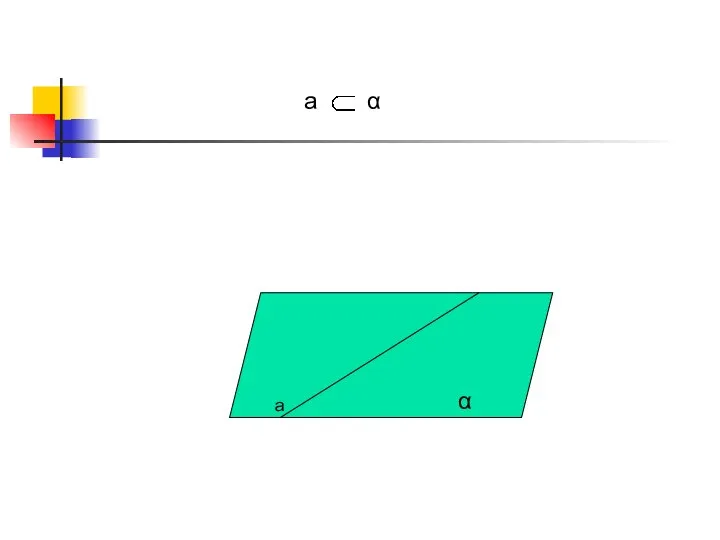
- 3. Прямая a Строчные латинские буквы a, b, c, d, e, k, …
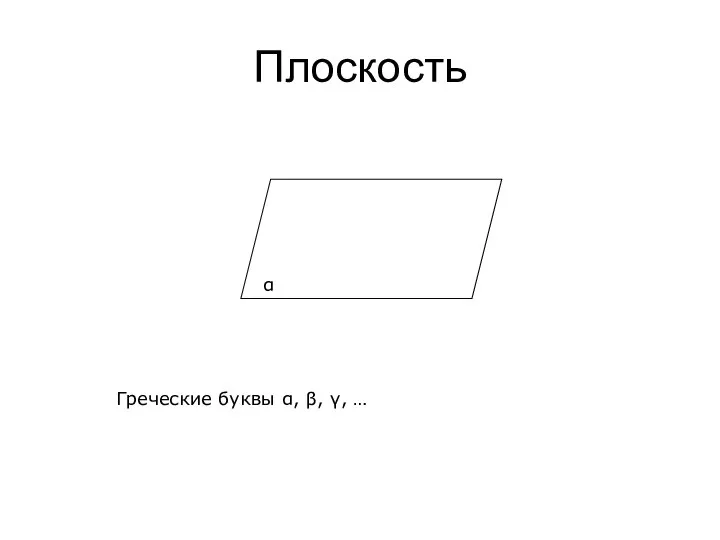
- 4. Плоскость α Греческие буквы α, β, γ, …
- 5. Взаимное расположение точек, прямых, плоскостей в пространстве.
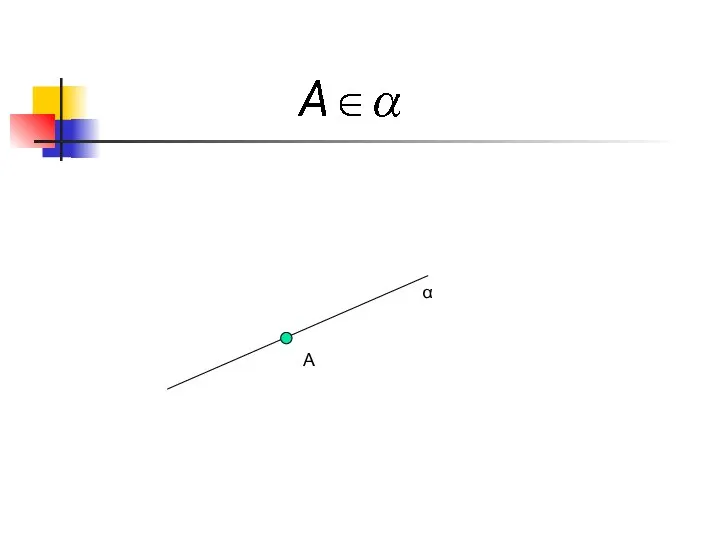
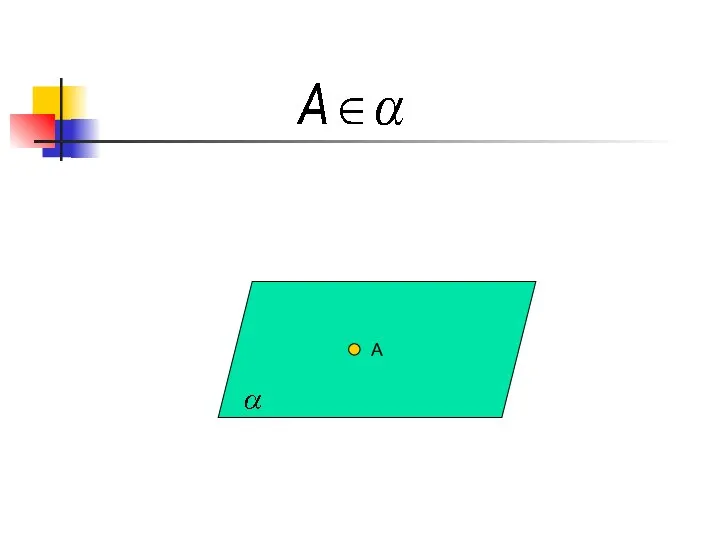
- 6. A α
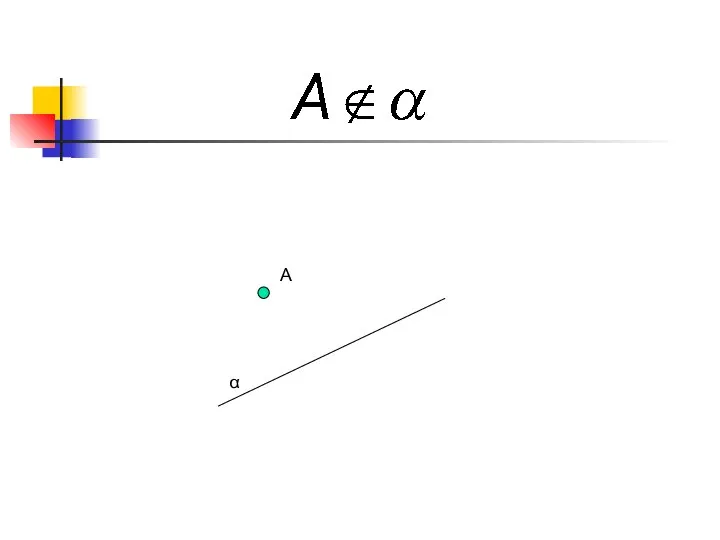
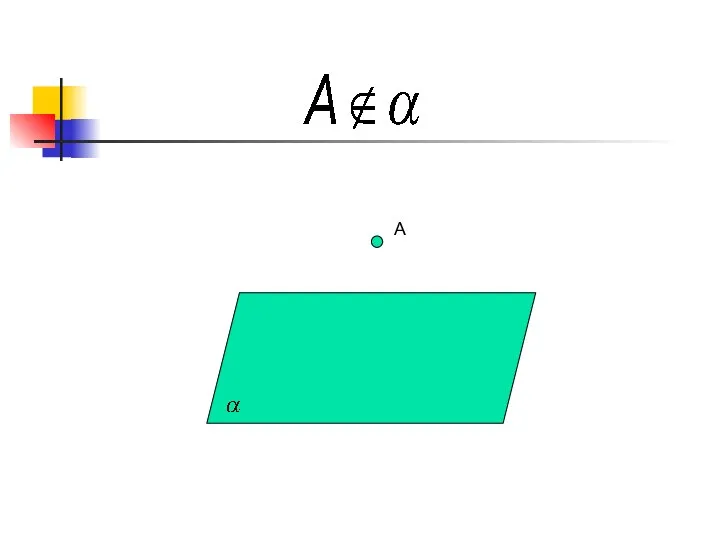
- 7. α A
- 8. A
- 9. A
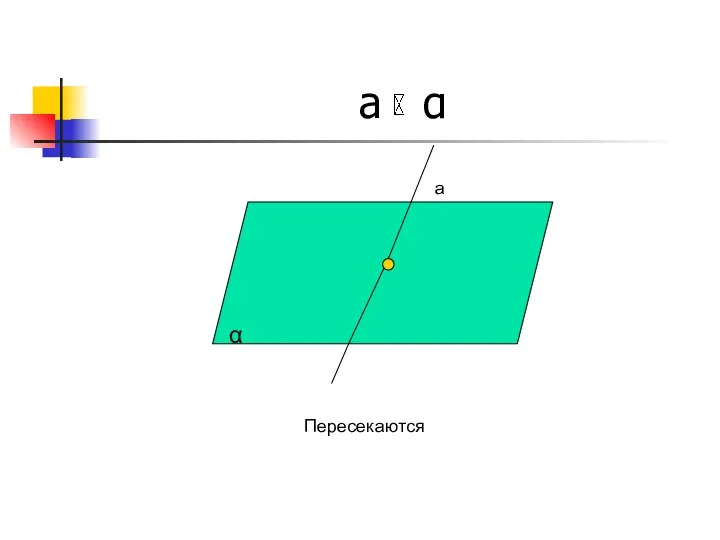
- 10. a α a α
- 11. a α a Пересекаются α
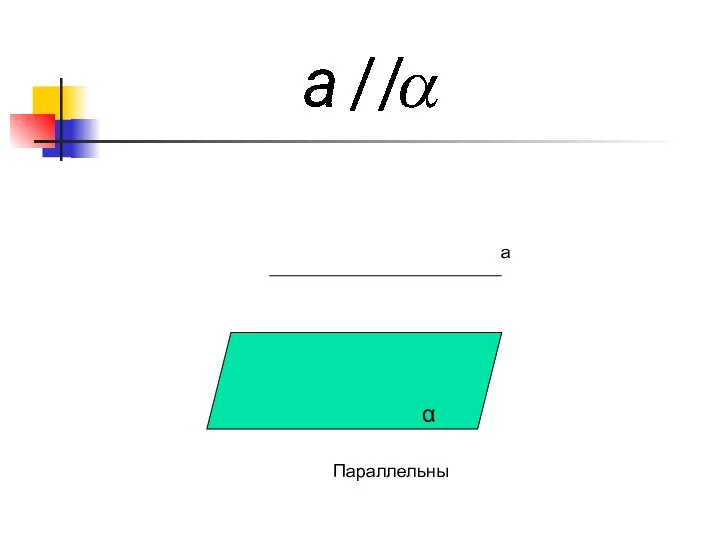
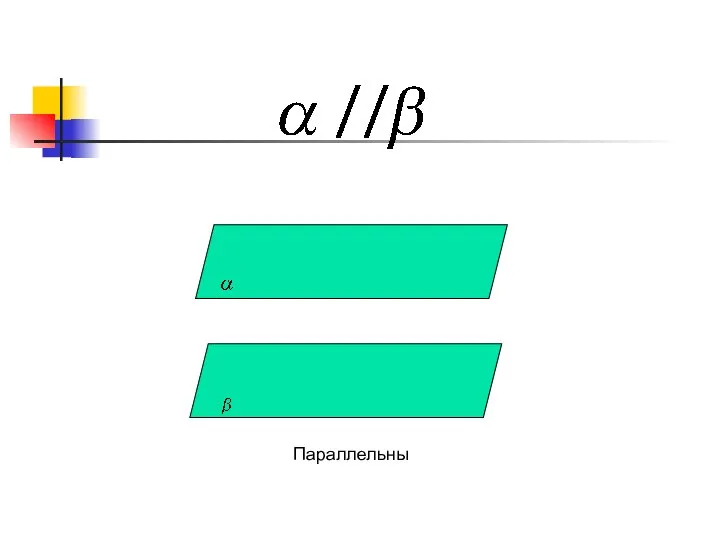
- 12. a Параллельны α
- 13. a||b a b
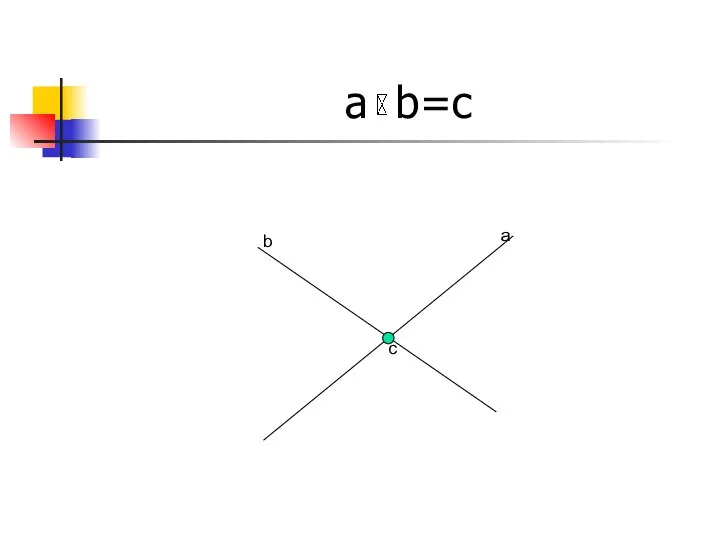
- 14. a b=c a b c
- 15. Параллельны
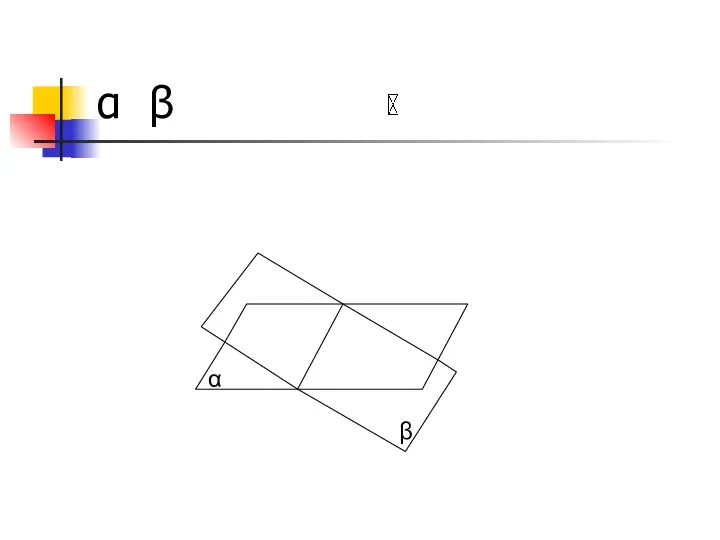
- 16. α β α β
- 17. Аксиомы стереометрии
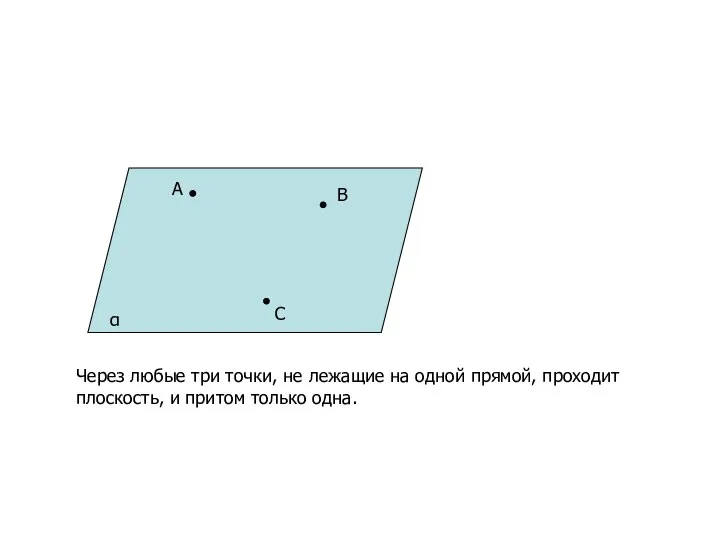
- 18. A B C α Через любые три точки, не лежащие на одной прямой, проходит плоскость, и
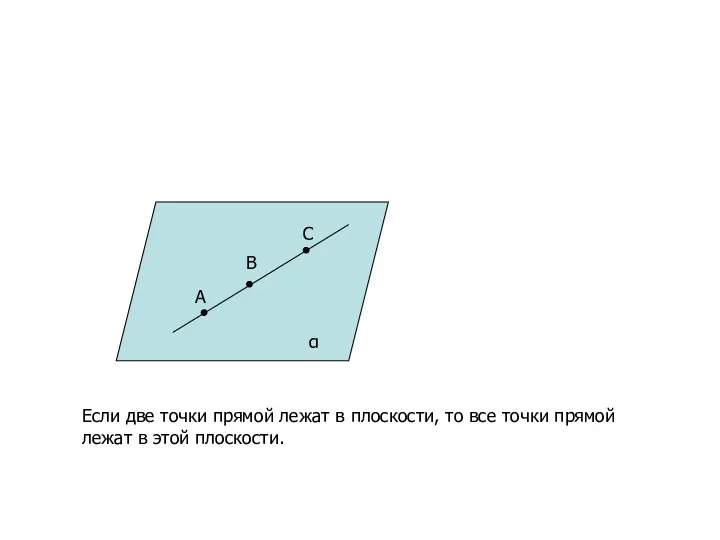
- 19. A B C α Если две точки прямой лежат в плоскости, то все точки прямой лежат
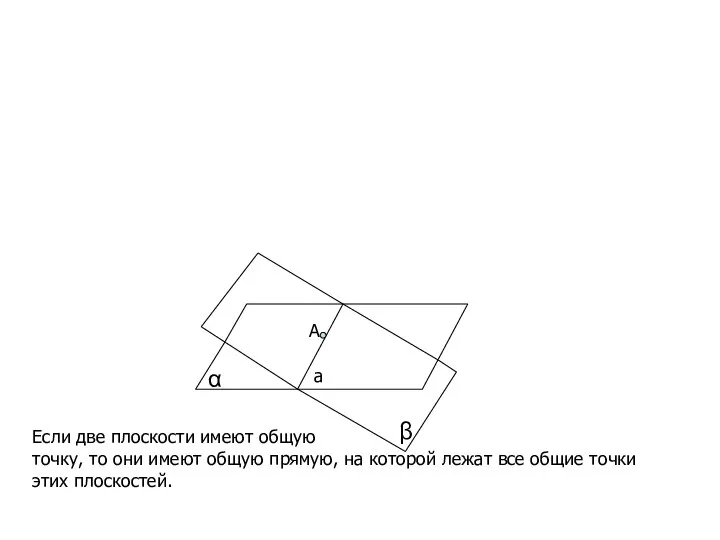
- 20. α β Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
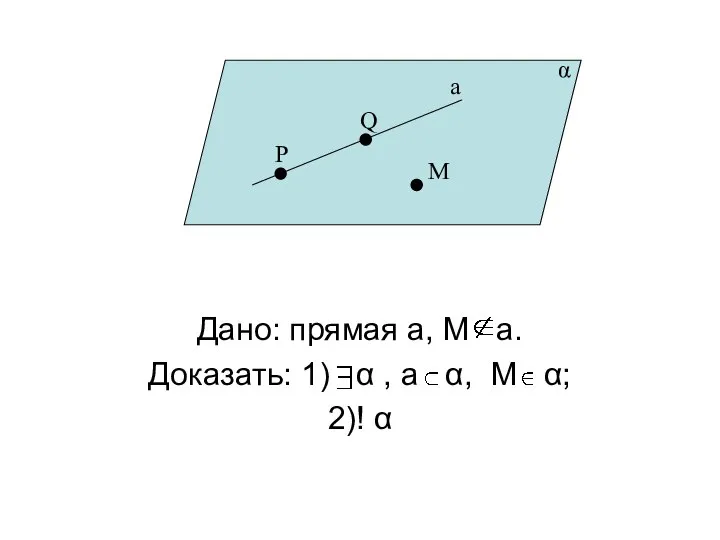
- 21. Следствия из аксиом стереометрии. Теорема 1.Через прямую и не лежащую на ней точку проходит плоскость, и
- 22. Дано: прямая а, М a. Доказать: 1) α , а α, М α; 2)! α P
- 23. Доказательство. Возьмем точки Р a, Q a.По А1 α, Р α,Q α, М α. Так как
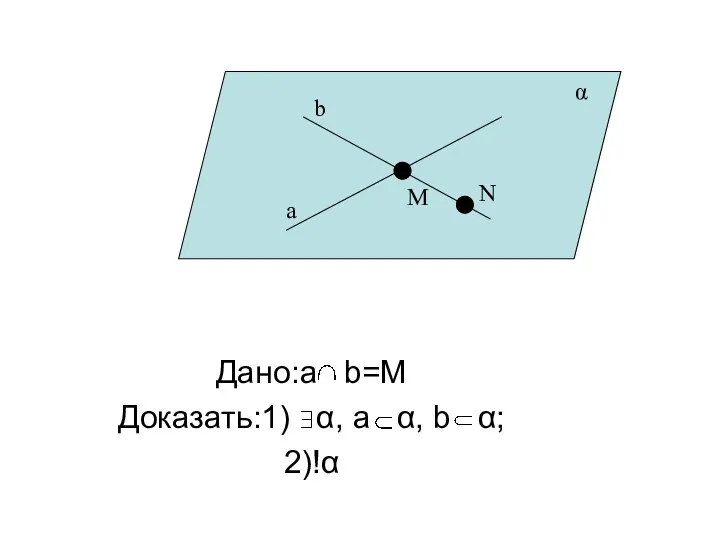
- 24. Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
- 25. Дано:a b=M Доказать:1) α, а α, b α; 2)!α a b M N α
- 26. Доказательство Возьмем точку N b. По Т1 α, а α,N α. Так как N b,M b
- 27. Способы задания плоскости в пространстве
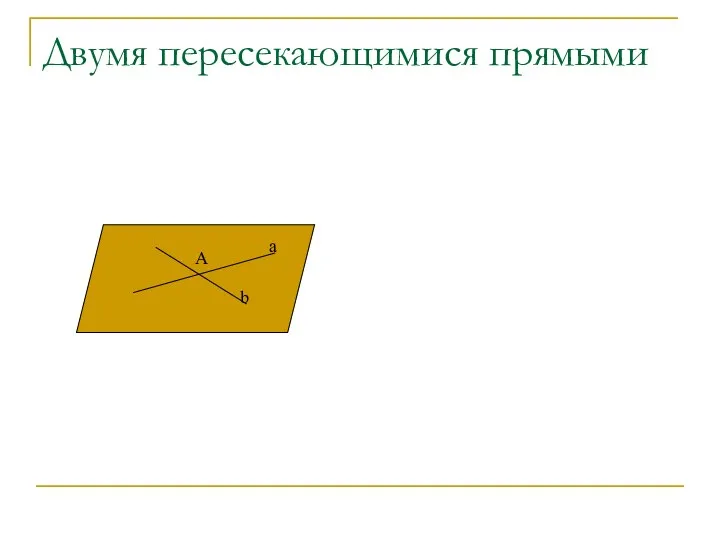
- 28. Двумя пересекающимися прямыми A a b
- 29. Тремя точками, не лежащими на одной прямой A B C
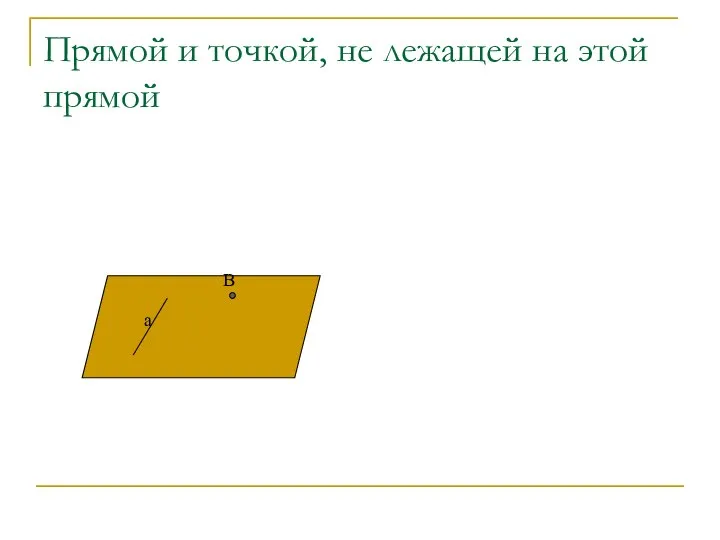
- 30. Прямой и точкой, не лежащей на этой прямой B a
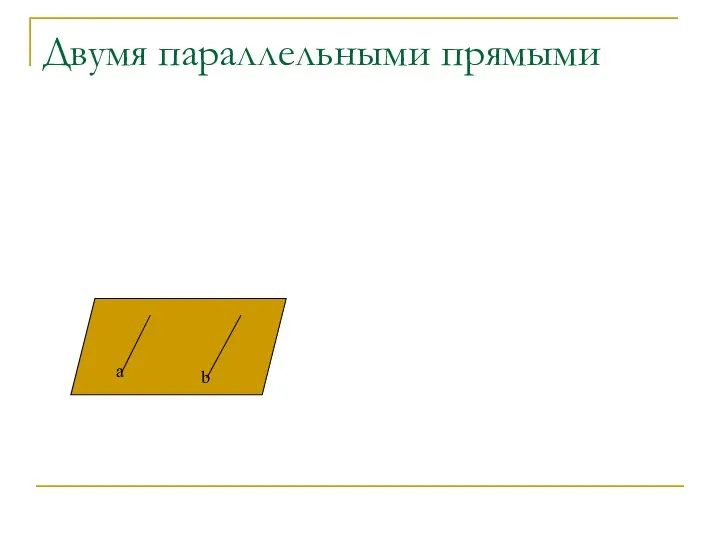
- 31. Двумя параллельными прямыми a b
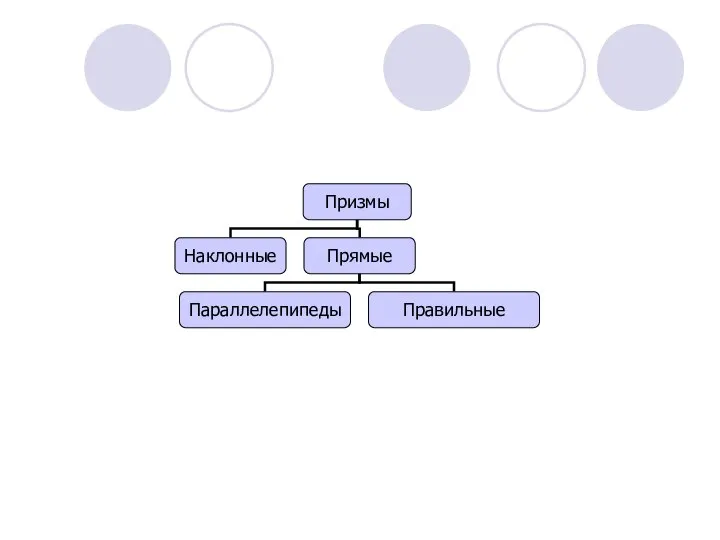
- 32. Многогранники. Тела вращения.
- 37. Скачать презентацию













 Презентация по геометрии Декартовы координаты
Презентация по геометрии Декартовы координаты  Презентация по геометрии Объем цилиндра
Презентация по геометрии Объем цилиндра Правильный шестиугольник
Правильный шестиугольник Чевианы треугольника Свойства медиан
Чевианы треугольника Свойства медиан Площади плоских фигур - презентация по Геометрии
Площади плоских фигур - презентация по Геометрии Икона «Троица» Андрея Рублева из собрания ГТГ. Презентация ученика 8 класса «Г» Краснова Артема. Руководитель – Михайловская Н.А
Икона «Троица» Андрея Рублева из собрания ГТГ. Презентация ученика 8 класса «Г» Краснова Артема. Руководитель – Михайловская Н.А Коллинеарные и компланарные векторы
Коллинеарные и компланарные векторы Понятие цилиндра - презентация по Геометрии
Понятие цилиндра - презентация по Геометрии Применение тригонометрии в жизни
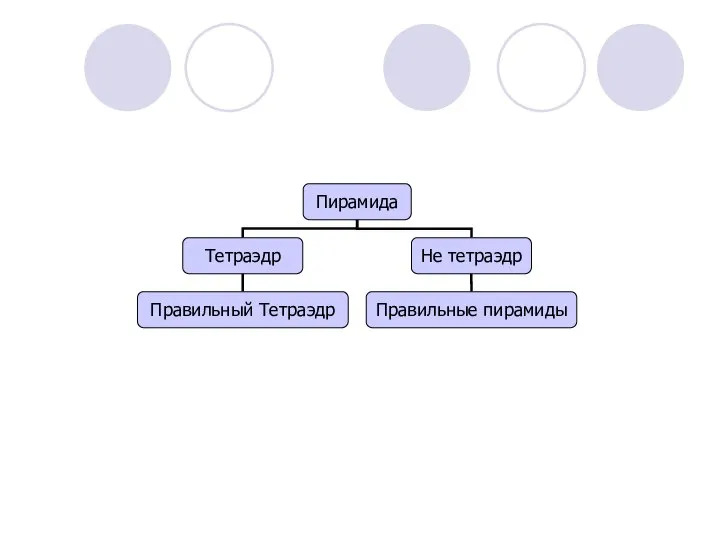
Применение тригонометрии в жизни  Правильные многоугольники
Правильные многоугольники  Работу выполнила ученица 10 класса МБОУ «Гимназия №2 г. Тосно» Хмыз Елизавета Руководитель Скалыга О.В.
Работу выполнила ученица 10 класса МБОУ «Гимназия №2 г. Тосно» Хмыз Елизавета Руководитель Скалыга О.В.  ТЕМА УРОКА: «Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник.» ЦЕЛИ УРОКА: Обоб
ТЕМА УРОКА: «Сложение, вычитание, умножение, деление натуральных чисел. Угол, треугольник, прямоугольник.» ЦЕЛИ УРОКА: Обоб Определение подобных треугольников - презентация по Геометрии
Определение подобных треугольников - презентация по Геометрии Решение задач с параметрами Выполнила: Матвиенко Елена Валентиновна – учитель математики ГООУ санаторной школы-интерната
Решение задач с параметрами Выполнила: Матвиенко Елена Валентиновна – учитель математики ГООУ санаторной школы-интерната  УРОК по теме «ТРЕУГОЛЬНИКИ» “Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг геометрия” французский архитектор Ле Корбюзье
УРОК по теме «ТРЕУГОЛЬНИКИ» “Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг геометрия” французский архитектор Ле Корбюзье Руководитель: Дрокова Татьяна Борисовна Авторы : «группа теоретиков» Романова Екатерина Гунин Артем Никитина Соф
Руководитель: Дрокова Татьяна Борисовна Авторы : «группа теоретиков» Романова Екатерина Гунин Артем Никитина Соф Движение - презентация по Геометрии
Движение - презентация по Геометрии Таблицы Геометрия 9 класс
Таблицы Геометрия 9 класс  Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры.
Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры.  Координатная прямая.
Координатная прямая. Сумма двух векторов. Геометрия 9 класс
Сумма двух векторов. Геометрия 9 класс Презентация к уроку ГЕОМЕТРИИ в 8 КЛАССЕ ПАРАЛЛЕЛОГРАММ
Презентация к уроку ГЕОМЕТРИИ в 8 КЛАССЕ ПАРАЛЛЕЛОГРАММ  Пирамида. Усечённая пирамида.
Пирамида. Усечённая пирамида. Можно ли наглядно представить себе четырехмерную фигуру? Построение гиперкуба.
Можно ли наглядно представить себе четырехмерную фигуру? Построение гиперкуба.  Тест по теме: «Признаки параллельности прямых. Свойства параллельных прямых»
Тест по теме: «Признаки параллельности прямых. Свойства параллельных прямых» Задачи на построение сечений многогранников
Задачи на построение сечений многогранников Презентация по геометрии на тему Конус
Презентация по геометрии на тему Конус Весёлая геометрия - презентация по Геометрии_
Весёлая геометрия - презентация по Геометрии_