Содержание
- 2. Вдохновение нужно в геометрии не меньше, чем в поэзии. А.С. Пушкин
- 3. Содержание Введение Сечение в разных областях Основные определения и понятия Базовые задачи Примеры Методы Литература
- 4. При изучении курса стереометрии большое значение имеет изображение пространственных фигур. При построении рисунка, изображающего пространственную фигуру,
- 5. Актуальность темы Выбор темы обусловлен, тем что: Изображение пространственных фигур на плоскости является одной из наиболее
- 6. Цель работы: познакомить со способами построения сечений многогранников, способствовать развитию пространственных представлений, выработке практических навыков в
- 7. Сечения в медицине
- 8. Сечения в истории и археологии
- 9. Сечения в архитектуре Золотое сечение пирамиды Хеопса
- 10. Основные определения Сечением многогранника P плоскостью называется фигура, состоящая из общих точек многогранника P и плоскости
- 11. При построении сечения многогранника, плоскостью α следует иметь в виду, что: Построение сечения сводится к построению
- 12. Осуществляя контроль за правильностью построения сечений многогранника, следует иметь в виду, что: если многогранник выпуклый, то
- 13. Осуществляя контроль за правильностью построения сечений многогранника, следует иметь в виду, что: Если многогранник выпуклый, то
- 14. Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения
- 15. MєABC, NєSBC, C; SABC-тетраэдр. C є ABC, Mє ABC, CM∩AB=P. C є SBC, N є SBC,
- 16. II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Базовые задачи
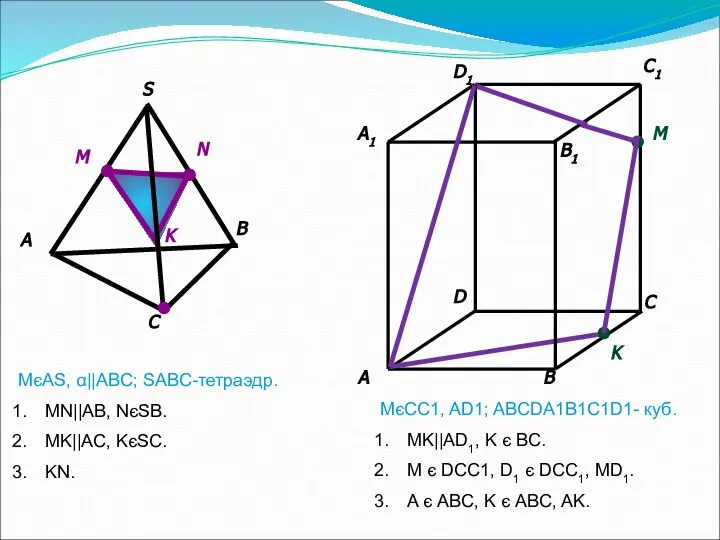
- 17. MєAS, α||ABC; SABC-тетраэдр. MN||AB, NєSB. MK||AC, KєSC. KN. MєCC1, AD1; ABCDA1B1C1D1- куб. MK||AD1, K є BC.
- 18. III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер
- 19. MєSA, NєSB, KєBC, SABC-тетраэдр. 1 Плоскости α, SAB, ABC образуют трехгранный угол, вершиной которого является точка
- 20. MєAB, NєAA1, KєA1D1; ABCDA1B1C1D1-куб. NK∩AD=F1 - вершина трехгранного угла образованного плоскостями α, ABC, ADD1. F1M∩CD=F2 -
- 21. Примеры решения задач 1) Сечение параллелепипеда по трем точкам, лежащим на трех параллельных ребрах (случай 1)
- 22. Q М R P N A B C D A1 B1 C1 D1 Построение: Отрезок MN.
- 23. P N М A B C A1 C1 D1 B1 D Q Построение: Отрезок MN. Отрезок
- 24. Строим сечение параллелепипеда по трем точкам, не лежащим на трех параллельных ребрах (случай 1) М Q
- 25. Строим сечение параллелепипеда по трем точкам, лежащим на трех соседних ребрах. N М P A B
- 26. Верно ли построено сечение? М N Q A B C A1 C1 D1 D B1 P
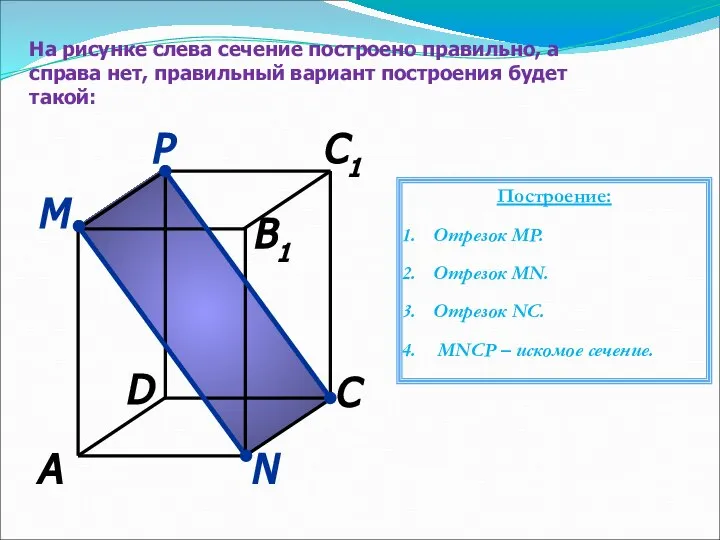
- 27. На рисунке слева сечение построено правильно, а справа нет, правильный вариант построения будет такой: М N
- 28. Небольшой тренинг для самопроверки Построить сечения, проходящее через данные точки
- 29. Все рассмотренные ранее построения плоских сечений многогранников осуществлялись на основании аксиом стереометрии и теорем о параллельности
- 30. Метод следов Определение: Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости
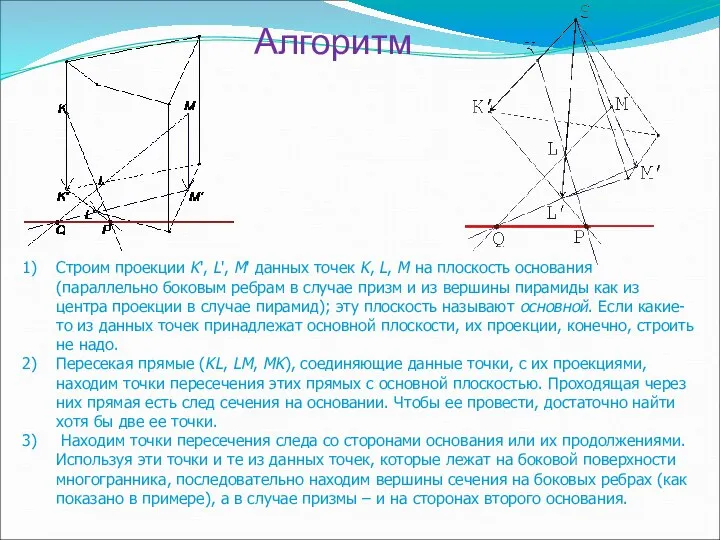
- 31. Алгоритм Строим проекции K', L', M' данных точек K, L, M на плоскость основания (параллельно боковым
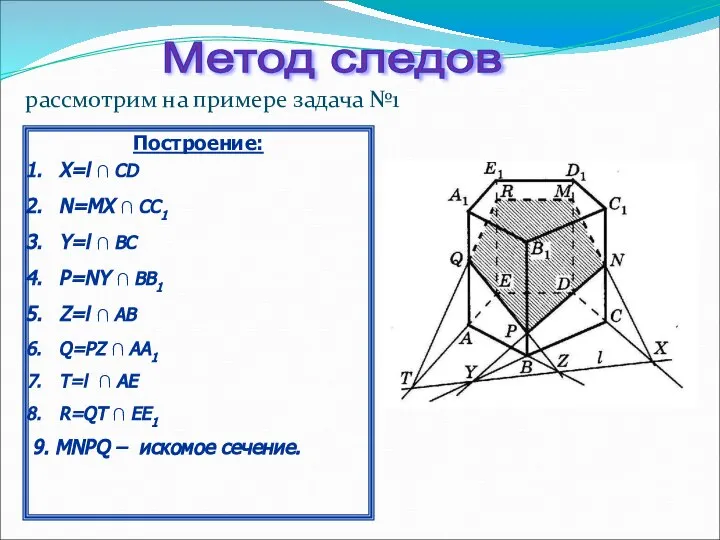
- 32. рассмотрим на примере задача №1 Метод следов Построение: Х=l ∩ CD N=MX ∩ CC1 Y=l ∩
- 33. Небльшой тренинг на метод следов
- 35. Метод внутреннего проектирования В некоторых учебных пособиях метод построения сечений многогранников, который мы сейчас будем рассматривать,
- 36. Алгоритм построения сечения методом внутреннего проектирования. Построить вспомогательные сечения и найти линию их пересечения. Построить след
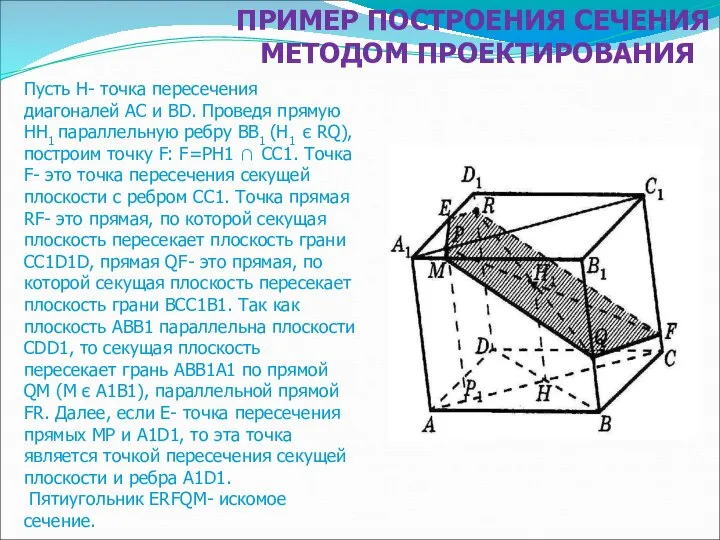
- 37. Пусть H- точка пересечения диагоналей AC и BD. Проведя прямую HH1 параллельную ребру BB1 (H1 є
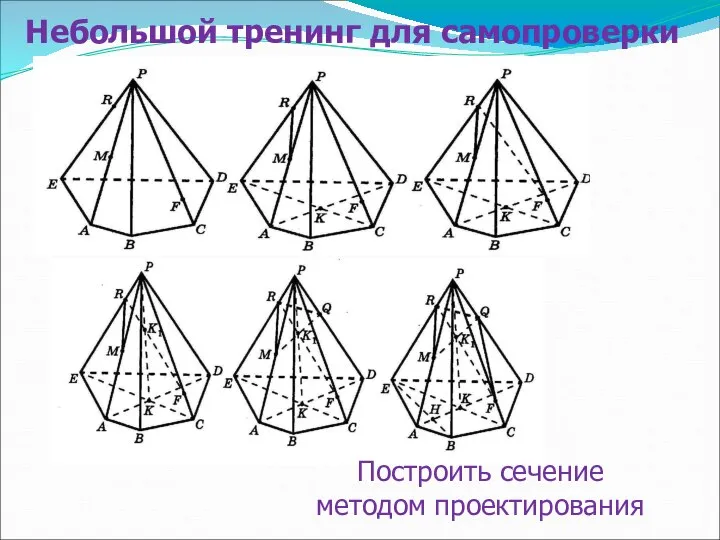
- 38. Небольшой тренинг для самопроверки Построить сечение методом проектирования
- 39. Комбинированный метод Сущность комбинированного метода построения сечений многогранников состоит в том, что на некоторых этапах построения
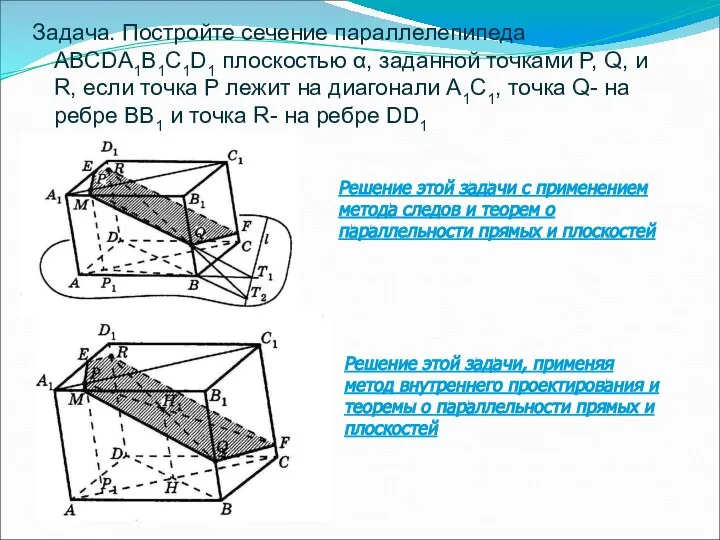
- 40. Задача. Постройте сечение параллелепипеда ABCDA1B1C1D1 плоскостью α, заданной точками P, Q, и R, если точка P
- 42. Скачать презентацию































 Зачем нужна наука геометрия? - презентация по Геометрии
Зачем нужна наука геометрия? - презентация по Геометрии Содержат алгоритм решения. Презентация подготовлена учителем математики МОУ «СОШ№6» п. Передового Богдановской В.М. и учеником 11
Содержат алгоритм решения. Презентация подготовлена учителем математики МОУ «СОШ№6» п. Передового Богдановской В.М. и учеником 11 Построение правильного шестиугольника 9 класс, геометрия Урок изучения новой темы
Построение правильного шестиугольника 9 класс, геометрия Урок изучения новой темы Презентация по геометрии ГЕОМЕТРИЯ Векторы в пространстве
Презентация по геометрии ГЕОМЕТРИЯ Векторы в пространстве  Учитель: Л.М.Осипова Ивня 2010 год
Учитель: Л.М.Осипова Ивня 2010 год Объёмы геометрических тел - презентация по Геометрии
Объёмы геометрических тел - презентация по Геометрии Применение подобия к доказательству теорем и решению задач
Применение подобия к доказательству теорем и решению задач Тайна магического квадрата. Выполнил ученик 6 класса: Ёркин Дмитрий Учитель: Ёркина А.М.
Тайна магического квадрата. Выполнил ученик 6 класса: Ёркин Дмитрий Учитель: Ёркина А.М. ГРАФА - презентация по Геометрии
ГРАФА - презентация по Геометрии Преобразование фигур
Преобразование фигур Длина окружности - презентация по Геометрии
Длина окружности - презентация по Геометрии Наглядная геометрия - презентация по Геометрии
Наглядная геометрия - презентация по Геометрии Геометрия Лобачевского - презентация по Геометрии
Геометрия Лобачевского - презентация по Геометрии ЧТО ТАКОЕ ГЕОМЕТРИЯ? Историческая справка
ЧТО ТАКОЕ ГЕОМЕТРИЯ? Историческая справка  Лабораторный практикум по геометрии 7 класс Учитель математики и физики моу Ромненская сош Русина Г.С.
Лабораторный практикум по геометрии 7 класс Учитель математики и физики моу Ромненская сош Русина Г.С.  (фантазия на тему «МНОГОГРАННИКИ») «В огромном саду геометрии каждый найдет букет себе по вкусу.» Д. Гильберт
(фантазия на тему «МНОГОГРАННИКИ») «В огромном саду геометрии каждый найдет букет себе по вкусу.» Д. Гильберт 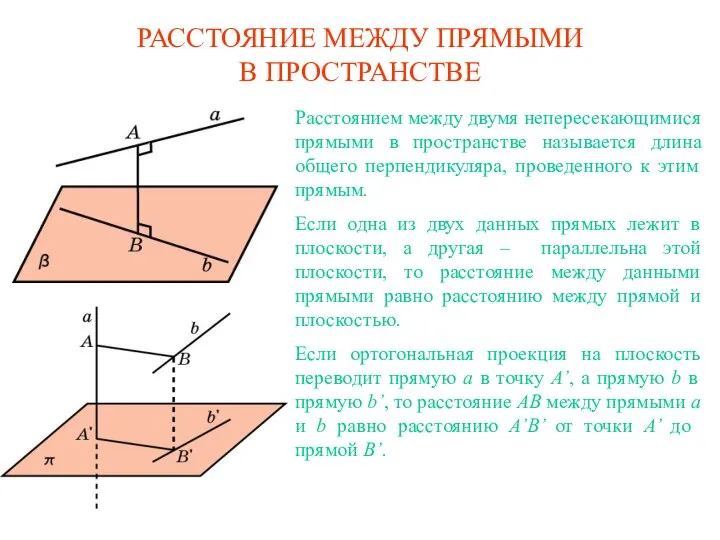 РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Объем прямой призмы
Объем прямой призмы  Наглядная геометрия для начальной школы
Наглядная геометрия для начальной школы  Геометрия в жизни (многогранники). Выполнил ученик 6Б класса средней школы № 165 Врачев Леонид
Геометрия в жизни (многогранники). Выполнил ученик 6Б класса средней школы № 165 Врачев Леонид  Признаки равенства треугольников. Устные задачи - презентация по Геометрии______________________________________________________________________________________________________
Признаки равенства треугольников. Устные задачи - презентация по Геометрии______________________________________________________________________________________________________ Симметрия: центральная и осевая Интегрированный урок по математике, биологии и информатике, 6 класс
Симметрия: центральная и осевая Интегрированный урок по математике, биологии и информатике, 6 класс Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна
Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна Тела вращения
Тела вращения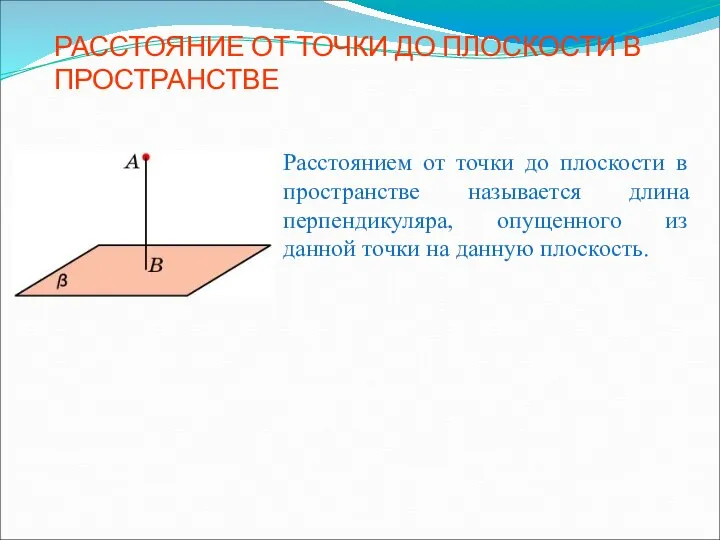 Расстояние от точки до плоскости в пространстве - презентация по Геометрии_
Расстояние от точки до плоскости в пространстве - презентация по Геометрии_ Прямоугольный треугольник - презентация по Геометрии
Прямоугольный треугольник - презентация по Геометрии ПРАВИЛЬНЫЕ МНОГОГРАННИКИ _
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ _ ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ Презентация учителя математики МОУ Чернышихинской СОШ Кулькиной Любови Викторовны
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ Презентация учителя математики МОУ Чернышихинской СОШ Кулькиной Любови Викторовны