Содержание
- 2. О решении задач на построение Решение задач на построение состоит из 4 этапов: Анализ Построение Доказательство
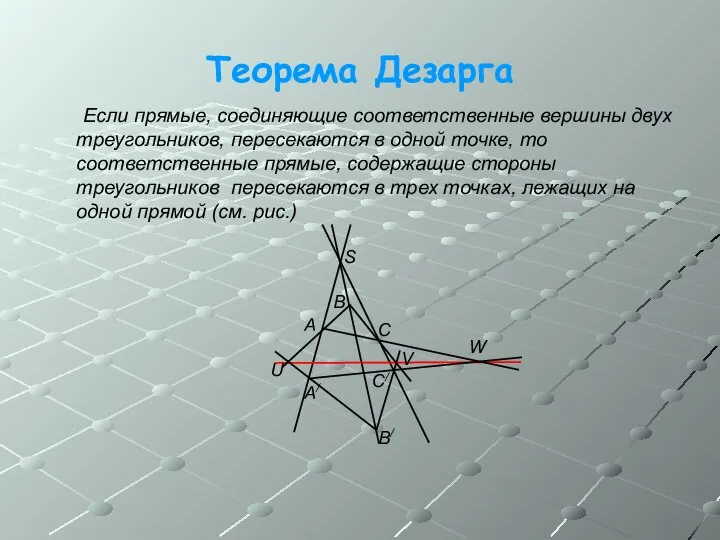
- 3. Теорема Дезарга Если прямые, соединяющие соответственные вершины двух треугольников, пересекаются в одной точке, то соответственные прямые,
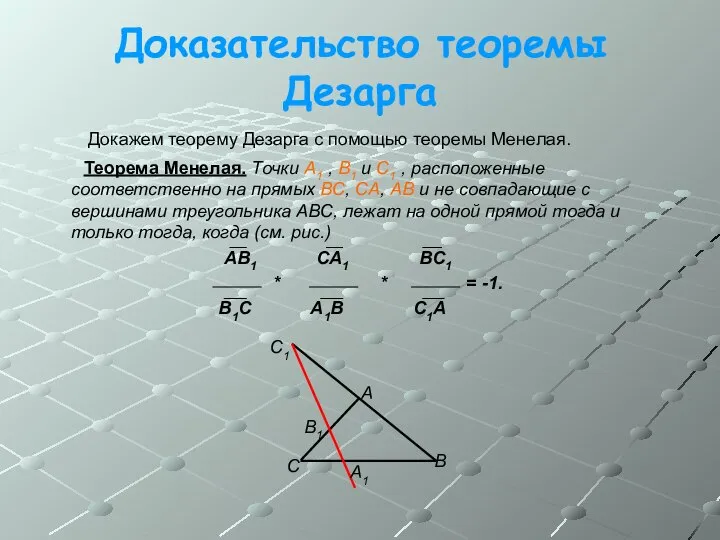
- 4. Доказательство теоремы Дезарга Докажем теорему Дезарга с помощью теоремы Менелая. Теорема Менелая. Точки A1 , B1
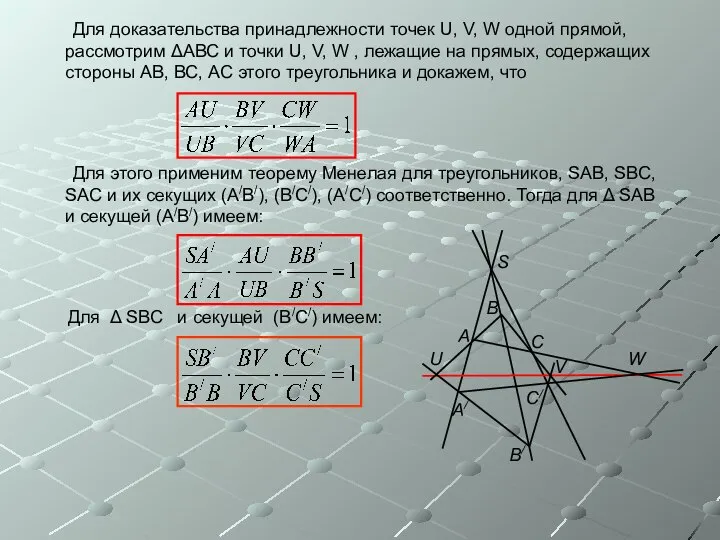
- 5. Для доказательства принадлежности точек U, V, W одной прямой, рассмотрим ΔАВС и точки U, V, W
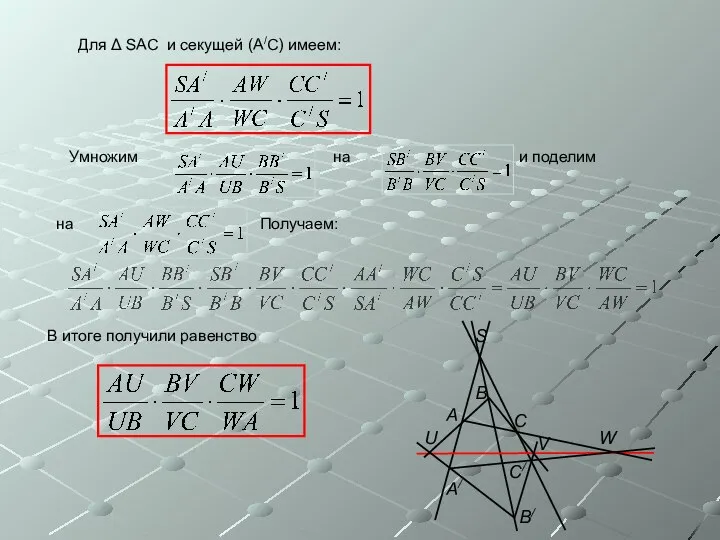
- 6. Для Δ SАС и секущей (А/С) имеем: Умножим на и поделим на Получаем: В итоге получили
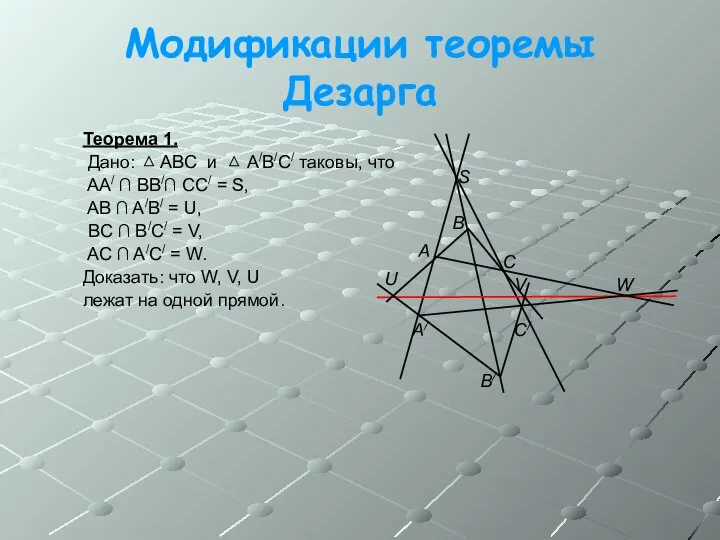
- 7. Модификации теоремы Дезарга Теорема 1. Дано: ABC и A/B/C/ таковы, что AA/ ∩ BB/∩ CC/ =
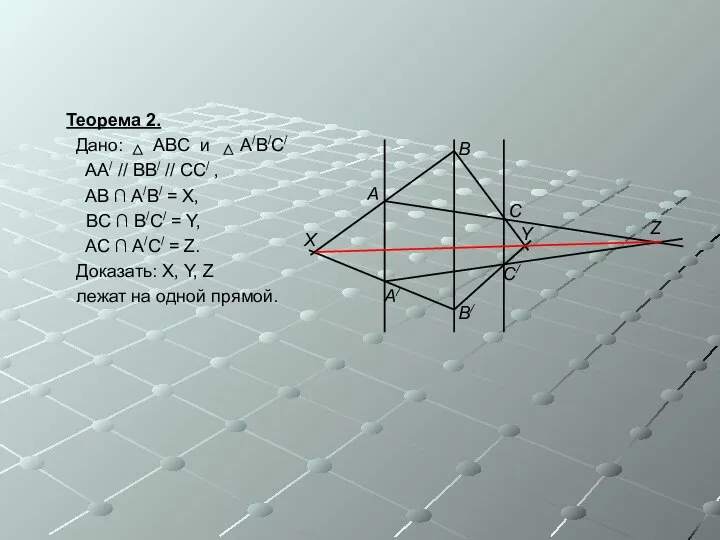
- 8. Теорема 2. Дано: ABC и A/B/C/ AA/ // BB/ // CC/ , AB ∩ A/B/ =
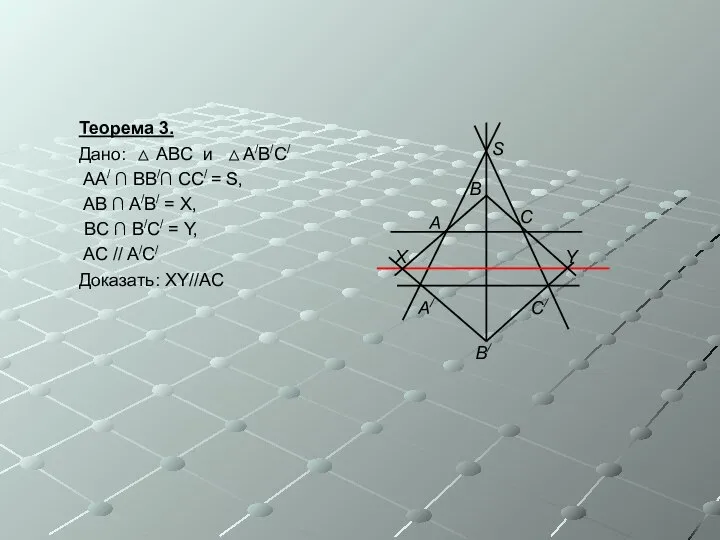
- 9. Теорема 3. Дано: ABC и A/B/C/ AA/ ∩ BB/∩ CC/ = S, AB ∩ A/B/ =
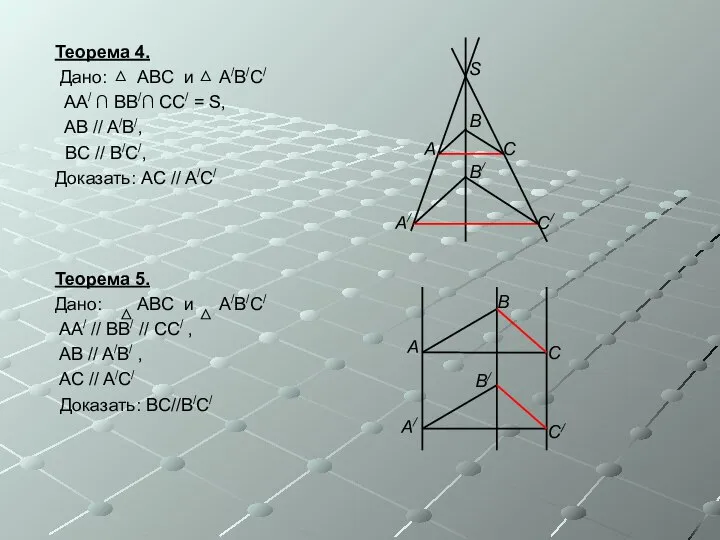
- 10. Теорема 4. Дано: ABC и A/B/C/ AA/ ∩ BB/∩ CC/ = S, AB // A/B/, BC
- 11. Применение теоремы Дезарга для построения параллельных прямых (с помощью одной линейки) Задача. Даны две различные параллельные
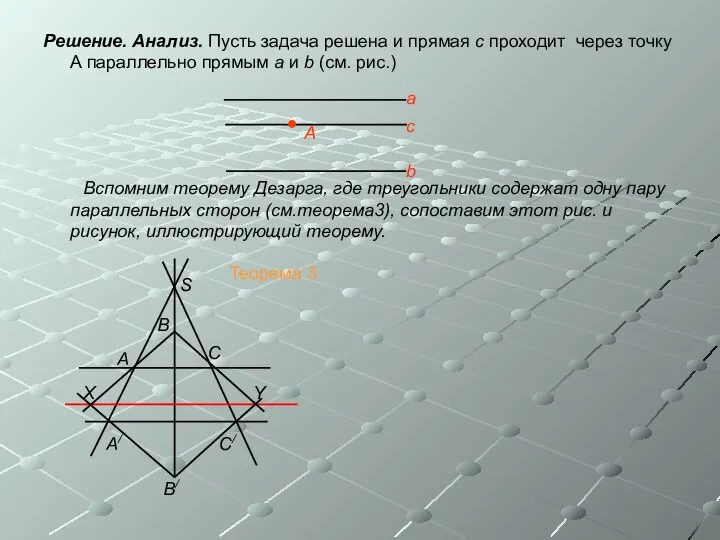
- 12. Решение. Анализ. Пусть задача решена и прямая с проходит через точку А параллельно прямым а и
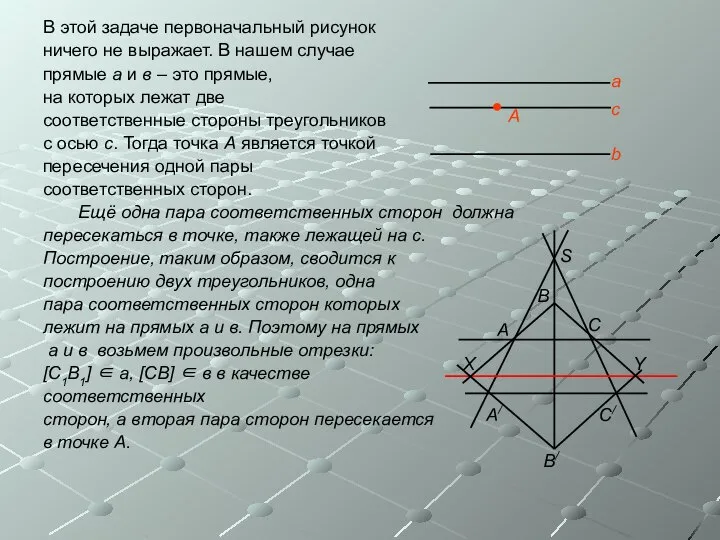
- 13. В этой задаче первоначальный рисунок ничего не выражает. В нашем случае прямые а и в –
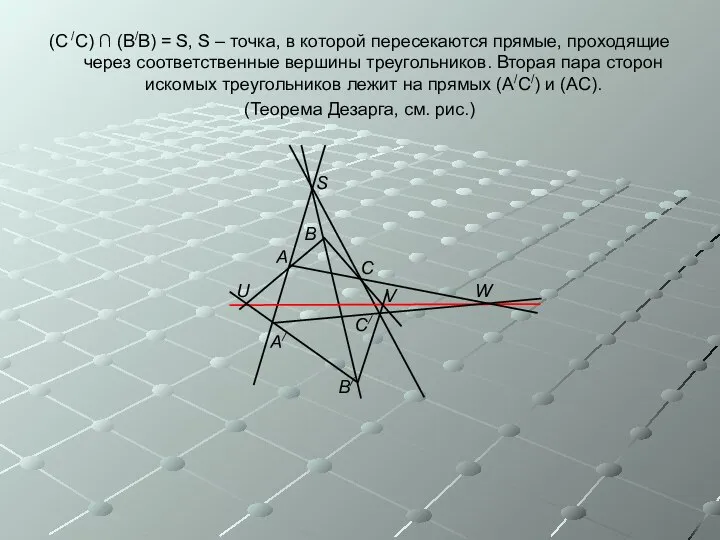
- 14. (С /С) ∩ (В/В) = S, S – точка, в которой пересекаются прямые, проходящие через соответственные
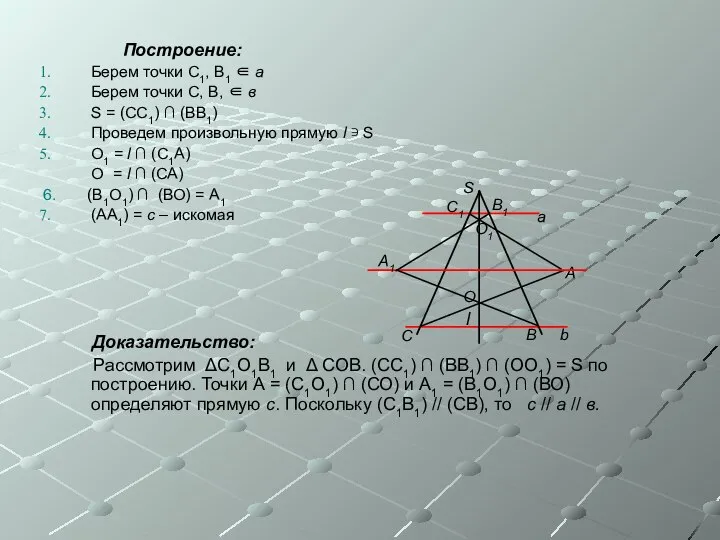
- 15. Построение: Берем точки С1, В1 ∈ а Берем точки С, В, ∈ в S = (СС1)
- 16. Исследование: Задача всегда имеет единственное решение, так как через данную точку можно провести единственную прямую, параллельную
- 17. Задача с недоступными элементами Точку называют недоступной, если к ней нельзя применить аксиомы конструктивной геометрии, в
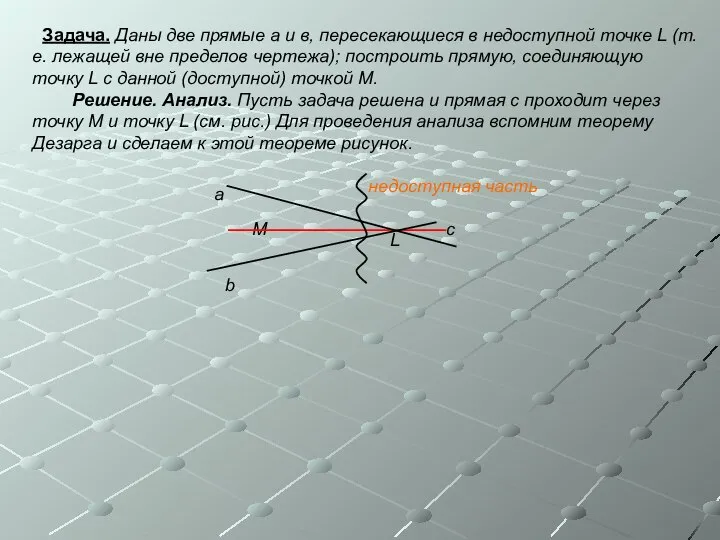
- 18. Задача. Даны две прямые а и в, пересекающиеся в недоступной точке L (т.е. лежащей вне пределов
- 19. Так как точки М и L лежат на одной прямой, то можно рассмотреть их как точки
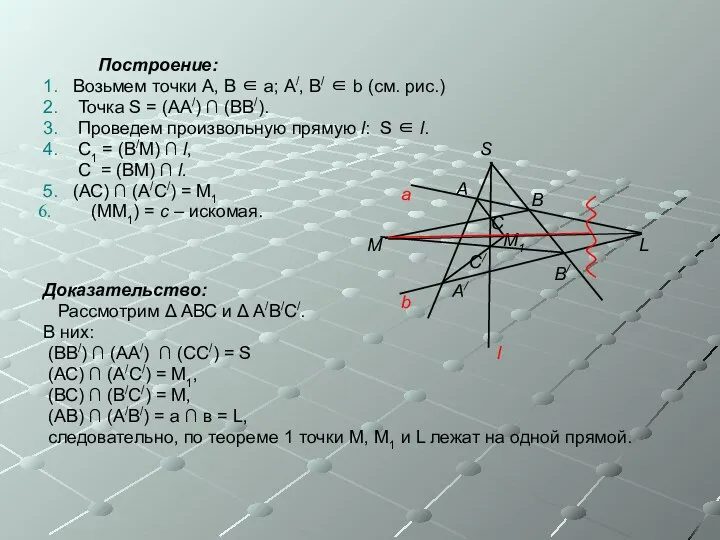
- 20. Построение: 1. Возьмем точки А, В ∈ а; А/, В/ ∈ b (см. рис.) 2. Точка
- 21. Поляра Четыре точки A, B, C, D, лежащие на одной прямой, образуют гармоническую четверку, если AC
- 22. Доказательство: Введем систему координат с началом в точке A, как показано на рисунке. Пусть B1, C1,
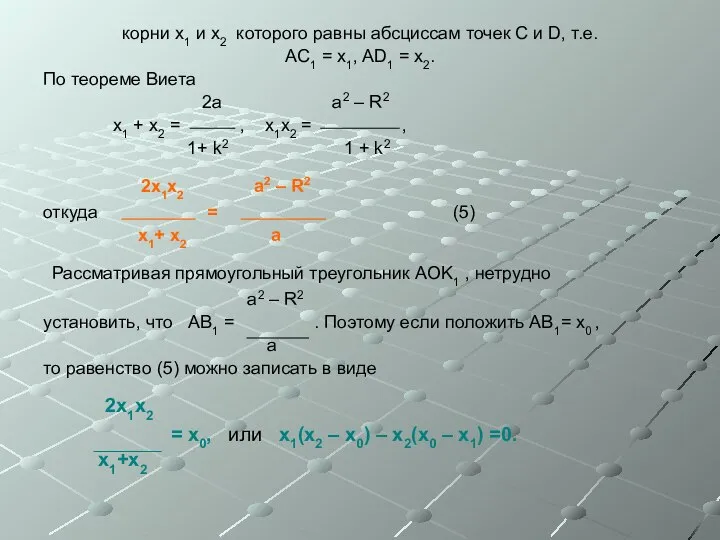
- 23. корни x1 и x2 которого равны абсциссам точек C и D, т.е. AC1 = x1, AD1
- 24. Отсюда, учитывая, что x1(x2 – x0) = AC1 * B1D1 , x2(x0 – x1) = AD1
- 26. Скачать презентацию








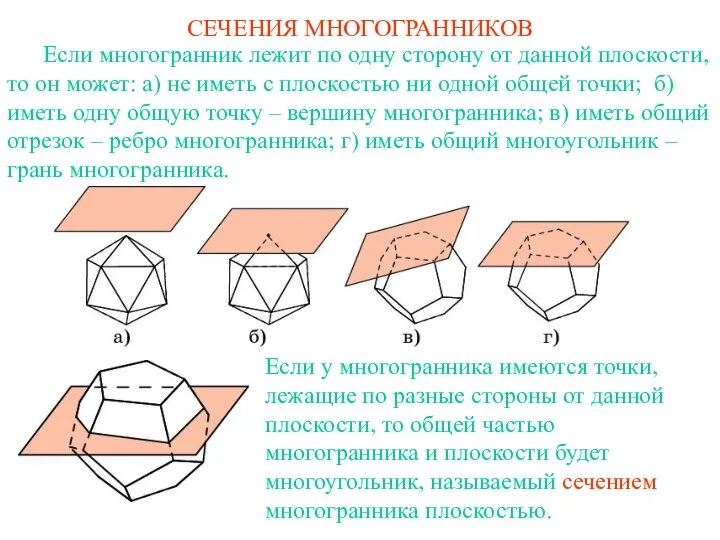 СЕЧЕНИЯ МНОГОГРАННИКОВ
СЕЧЕНИЯ МНОГОГРАННИКОВ Треугольники
Треугольники Геометрия путешествий
Геометрия путешествий Подобные треугольники - презентация по Геометрии
Подобные треугольники - презентация по Геометрии Темы: График квадратичной функции. Неравенства с одной переменной.
Темы: График квадратичной функции. Неравенства с одной переменной.  Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна
Измеряем длину окружности Школа № 254 Преподаватель Павлова Марина Константиновна Тема урока: « Объемы параллелепипеда и призмы» МБОУ Новоаннинская СОШ№4 Волгоградская область Карпова Ольга Васильевна
Тема урока: « Объемы параллелепипеда и призмы» МБОУ Новоаннинская СОШ№4 Волгоградская область Карпова Ольга Васильевна  Квадратичная функция и её график - презентация по Геометрии_
Квадратичная функция и её график - презентация по Геометрии_ Теорема Пифагора _
Теорема Пифагора _ Лобачевский и его геометрия - презентация по Геометрии
Лобачевский и его геометрия - презентация по Геометрии Moy”Коммунарский лицей” Тема: Геометрические фигуры в живописи. Выполнили: Гущина Анна и Осипова Анастасия.
Moy”Коммунарский лицей” Тема: Геометрические фигуры в живописи. Выполнили: Гущина Анна и Осипова Анастасия.  Трапеция
Трапеция Свойства прямоугольного параллелепипеда Лазарева Н.П., учитель математики МОУ С ОШ № 12
Свойства прямоугольного параллелепипеда Лазарева Н.П., учитель математики МОУ С ОШ № 12 Соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_____________________________________________________________________
Соотношения между сторонами и углами прямоугольного треугольника - презентация по Геометрии_____________________________________________________________________ Векторы в пространстве
Векторы в пространстве  Многогранники - презентация по Геометрии
Многогранники - презентация по Геометрии Первые шаги в геометрии Максимов Владислав Ярлыкова Александра Руководитель: Веременко Л.Л
Первые шаги в геометрии Максимов Владислав Ярлыкова Александра Руководитель: Веременко Л.Л Столбчатые диаграммы 6 класс Методическая разработка Васениной В.Ю. учителя математики Белохолуницкого района Кировской
Столбчатые диаграммы 6 класс Методическая разработка Васениной В.Ю. учителя математики Белохолуницкого района Кировской  Понятие движения Выполнил ученик 9 класса: Прусаков Денис
Понятие движения Выполнил ученик 9 класса: Прусаков Денис Анализ геометрической формы предмета
Анализ геометрической формы предмета РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ Координатным и векторным способом
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ Координатным и векторным способом  Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Василь
Работа по теме « Средняя линия трапеции» Ученика 9-2 класса Школы №593 Андреева Георгия Преподаватель : Петрова Наталья Василь Параллелограмм - презентация по Геометрии
Параллелограмм - презентация по Геометрии «Золотое сечение» (виртуальный факультатив) Составитель - Процко Т.М. – учитель математики МГМЛ при МГТУ им. Г.И.Носова
«Золотое сечение» (виртуальный факультатив) Составитель - Процко Т.М. – учитель математики МГМЛ при МГТУ им. Г.И.Носова Многогранники
Многогранники  Тема урока Тетраэдр и его сечения
Тема урока Тетраэдр и его сечения  Презентация по геометрии Теорема Пифагора Теорема обратная теореме Пифагора
Презентация по геометрии Теорема Пифагора Теорема обратная теореме Пифагора  Сфера. Шар - презентация по Геометрии_
Сфера. Шар - презентация по Геометрии_