_2._Kompleksnye_chisla

— действительная часть комплексного числа;

— мнимая часть комплексного числа.

Два комплексных числа

— число, комплексно сопряженное к

Свойства

Доказательство.

Пусть

1) Необходимость.

Если то т.е.

Пусть Докажем, что

Достаточность.

Пусть Докажем, что

Имеем,

4) Преобразуем левую часть:

Преобразуем правую часть:

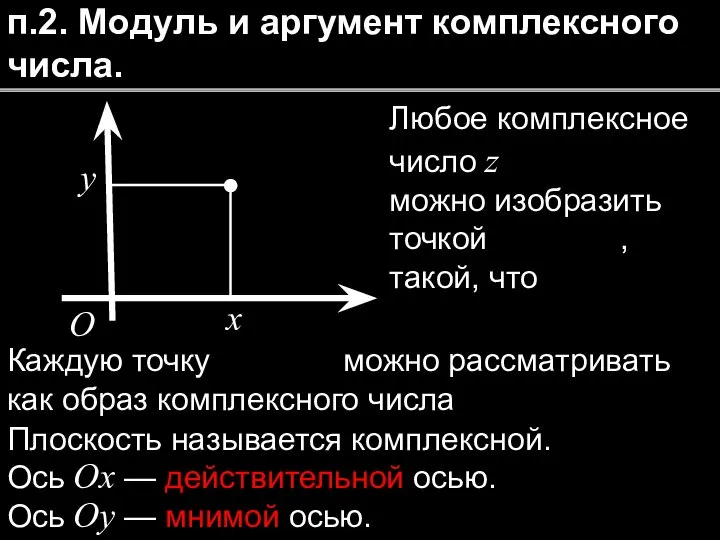
x

y

O

п.2. Модуль и аргумент комплексного числа.

Любое комплексное число z можно изобразить

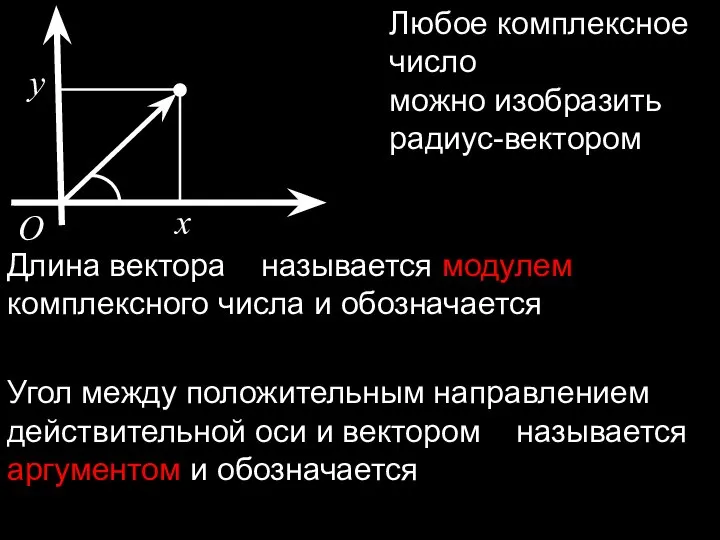
x

y

O

Любое комплексное число можно изобразить радиус-вектором

Длина вектора называется модулем комплексного

Значение аргумента, заключенное в границах

называют главным значением аргумента, и обозначают

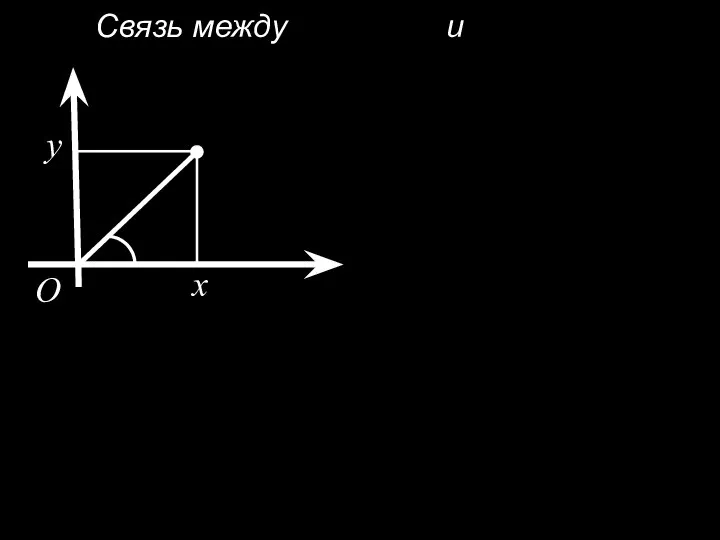
Связь между и

x

y

O

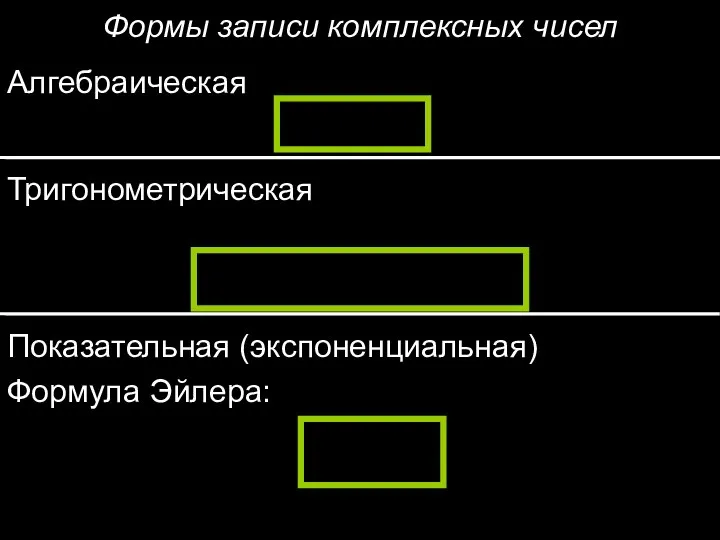
Формы записи комплексных чисел

Алгебраическая

Тригонометрическая

Показательная (экспоненциальная)

Формула Эйлера:

Замечание 4.

Пример 1. Записать комплексное число

в тригонометрической и показательной форме.

Решение.

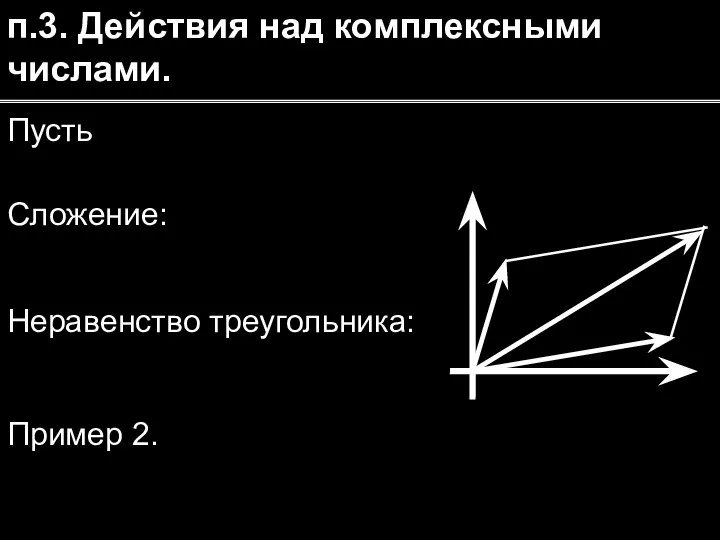
п.3. Действия над комплексными числами.

Пусть

Сложение:

Пример 2.

Неравенство треугольника:

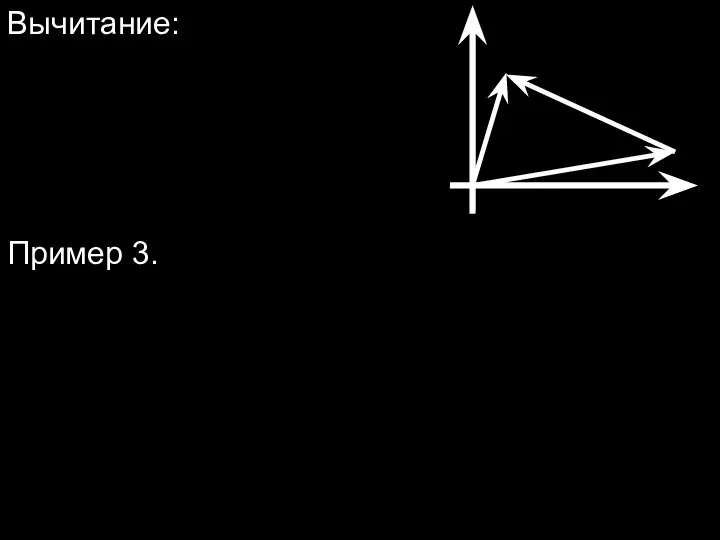
Вычитание:

Пример 3.

Умножение:

Пример 4.

Замечание 5.

Доказательство.

Умножение комплексных чисел в тригонометрической форме.

Пусть

Тогда

При умножении комплексных чисел их модули

Можно показать, что

Если

то

— формула Муавра.

Пример 5. Вычислить

Решение.

Деление:

Пример 6.

Деление комплексных чисел в тригонометрической форме.

Пусть

Тогда

При делении комплексных чисел их модули

Извлечение корня из комплексных чисел

Пусть

Корнем n-й степени из комплексного числа z

Учитывая замечание 3, получаем

Поэтому,

Получили n различных значений корня n-й степени из

Пример 7. Найти все значения

Решение.

Представим комплексное число в тригонометрической форме

Тогда