Содержание
- 2. Теория чисел: наука о числовых системах изучает числа с точки зрения их строения и внутренних связей,
- 3. Пифагорейские числа Совершенные, недостаточные и избыточные числа: недостаточные числа – те, сумма собственных делителей которых меньше
- 4. Числа близнецы Числа близнецы - пары простых чисел с разностью, равной двум (в пределах первой сотни):
- 5. Иога́нн Карл Фри́дрих Га́усс (1777 — 1855 гг.) — немецкий математик, механик, физик, астроном и геодезист
- 6. Отношение делимости. Делимость целых чисел В Италии существует поговорка «Трудное дело деление».Так обычно говорят, когда оказываются
- 7. Старинная восточная притча Давным-давно жил-был старик, который, умирая, оставил своим трём сыновьям 19 верблюдов. Он завещал
- 8. Старинная восточная притча - Нет ничего проще, - ответил им мудрец. – Возьмите моего верблюда и
- 9. Определение отношения делимости Пусть a, b ϵ Z, b≠0. Говорят, что a делится на b, если
- 10. На 0 делить нельзя Число 0 не рассматривается в качестве делителя Действительно, если a≠0, то a=0∙q
- 11. Пример Разложим в произведение выражение a2-a2 двумя способами: Имеем: а(а-а)=(а-а)(а+а) Разделим обе части на (а-а) и
- 12. Свойства делимости 1. , если а≠0 2. Если и , то 3. Если а≠0, то 4.
- 13. Свойства делимости Если и , то 9. Если и b ϵ Z, то 10. Если и
- 14. Теорема о делении с остатком Для любого целого числа а и любого целого b≠0 существуют и
- 15. Доказательство 1) b>0. Рассмотрим числовую прямую и разобьем её на отрезки длины b точками 0, ±b,
- 16. Доказательство Докажем единственность. Пусть a =bq+r, 0≤ r Имеем: bq+r = bq1+r1, b(q-q1) = r1-r Если
- 18. Скачать презентацию















 Презентация на тему Точки и линии. Прямая
Презентация на тему Точки и линии. Прямая  Волшебные часы
Волшебные часы Системы счисления в заданиях ОГЭ и ЕГЭ 2016
Системы счисления в заданиях ОГЭ и ЕГЭ 2016 Сфера
Сфера Площадь кругового сектора
Площадь кругового сектора Как люди считали в старину и как писали цифры
Как люди считали в старину и как писали цифры Решение задач по математике
Решение задач по математике Методические особенности школьного курса математики. (5-6 класс)
Методические особенности школьного курса математики. (5-6 класс)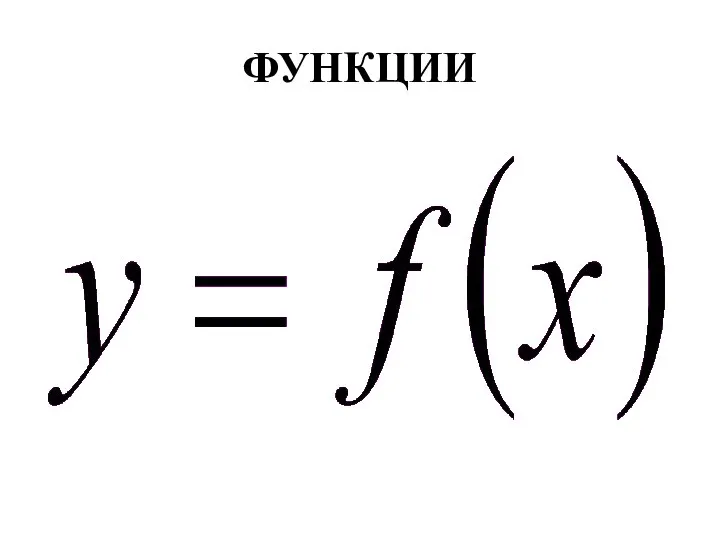 Функции. Способы задания функции
Функции. Способы задания функции Туындының анықтамасы
Туындының анықтамасы Понятие доли. Нахождение одной доли от целого
Понятие доли. Нахождение одной доли от целого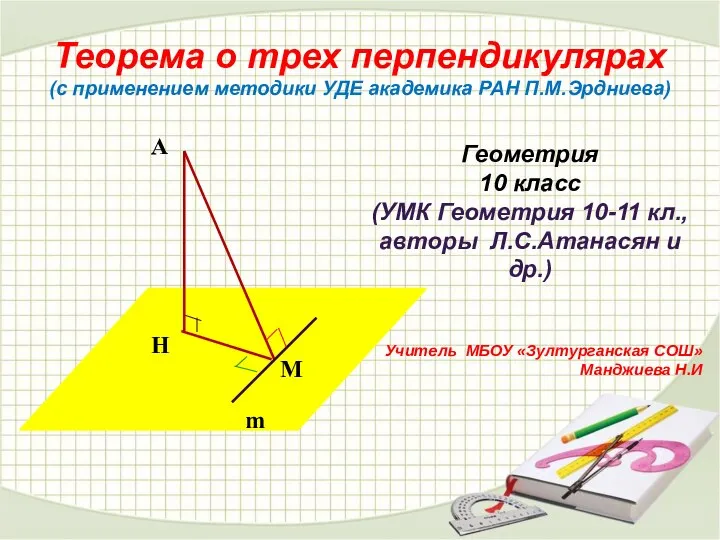 Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева)
Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева) Аттестационная работа. Образовательная программа элективного курса. Математика - абитуриенту. (11 класс)
Аттестационная работа. Образовательная программа элективного курса. Математика - абитуриенту. (11 класс) Презентация на тему Дискретный анализ Комбинаторика. Перестановки
Презентация на тему Дискретный анализ Комбинаторика. Перестановки  Взаимно обратные функции
Взаимно обратные функции Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰ Вписанная и описанная призмы. Задания
Вписанная и описанная призмы. Задания Математика 1 класс. Ломаные линии. Звено ломаной линии. Вершины
Математика 1 класс. Ломаные линии. Звено ломаной линии. Вершины Презентация по математике "Галерея великих" - скачать
Презентация по математике "Галерея великих" - скачать  УРОК МАТЕМАТИКИ В 4 А КЛАССЕ Составление примеров на деление. Линии. Попикова Наталья Александровна, учитель начальных класс
УРОК МАТЕМАТИКИ В 4 А КЛАССЕ Составление примеров на деление. Линии. Попикова Наталья Александровна, учитель начальных класс Тригонометрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень)
Тригонометрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень) Первообразная
Первообразная Преобразование выражений, содержащих радикалы
Преобразование выражений, содержащих радикалы Элементы теории множеств при работе с информацией
Элементы теории множеств при работе с информацией Наглядная геометрия. 5-6 классы
Наглядная геометрия. 5-6 классы Понятие функции
Понятие функции Интервальное оценивание параметров ( лекция 7)
Интервальное оценивание параметров ( лекция 7) Формула корней квадратного уравнения
Формула корней квадратного уравнения