Базовые задачи на построение сечений многогранников

от которой имеются точки данного многогранника.

Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.

точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей.

1.

2.

MєABC, NєSBC, C; SABC-тетраэдр.
CєABC, MєABC, CM∩AB=P.
CєSBC, NєSBC, CN∩SB=Q.
PєABS, QєABS, PQ.

MєAD, NєDCC1, D1; ABCDA1B1C1D1-куб
MєADD1, D1єADD1, MD1.
D1єD1DC, NєD1DC, D1N∩DC=Q.
MєABC, QєABC, MQ.

параллельны.

3.

4.

MєAS, α||ABC; SABC-тетраэдр.
MN||AB, NєSB.
MK||AC, KєSC.
KN.

MєCC1, AD1; ABCDA1B1C1D1-куб.
MK||AD1, KєBC.
MєDCC1, D1єDCC1, MD1.
AєABC, KєABC, AK.

линий их парного пересечения (ребер трехгранного угла).

5.

6.

MєSA, NєSB, KєBC, SABC-тетраэдр.
1. Плоскости α, SAB, ABC образуют трехгранный угол, вершиной которого является точка F. AB∩MN=F.
2. FK∩AC=P.
3. PєSAC, MєSAC, MP.

MєAB, NєAA1, KєA1D1; ABCDA1B1C1D1-куб.
NK∩AD=F1 - вершина трехгранного угла образованного плоскостями α, ABC, ADD1.
F1M∩CD=F2 - вершина трехгранного угла образованного плоскостями α, ABC, CDD1. F1M∩BC=P.
NK∩DD1=F3 - вершина трехгранного угла образованного плоскостями α, D1DC, ADD1.
F3F2∩D1C1=Q, F3F2∩CC1=L.

ее, то линия пересечения параллельна данной прямой.

7.

8.

MєSB, NєSAC, α||AB; SABC-тетраэдр.
1. α∩SAB=KM, KєSA, KM||AB.
2. KN∩AC=P.
3. α∩ABC=PQ, QєBC, PQ||AB.

A1, C,α||BC1; ABCA1B1C1-призма.
α∩BCC1=n, n||BC1, n∩BB1=S.
SA1∩AB=P.
Соединяем A1,P и C.

с плоскостью грани многогранника является вершиной трехгранного угла, образованного сечением, гранью и вспомогательной плоскостью, содержащей данную прямую.

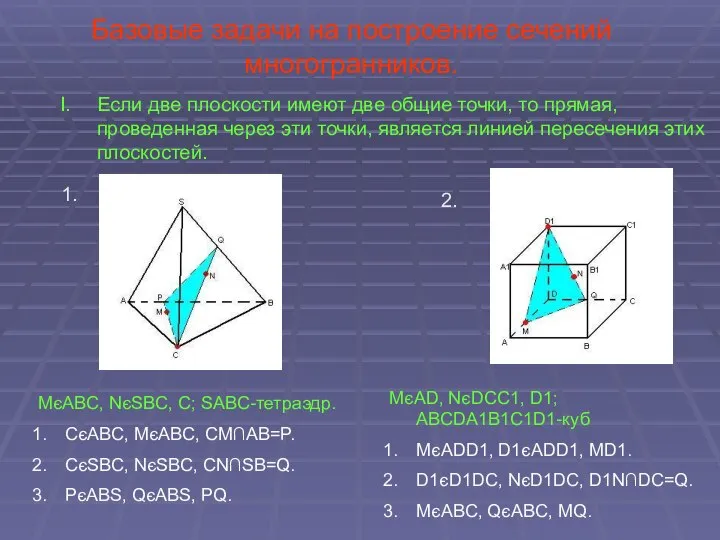
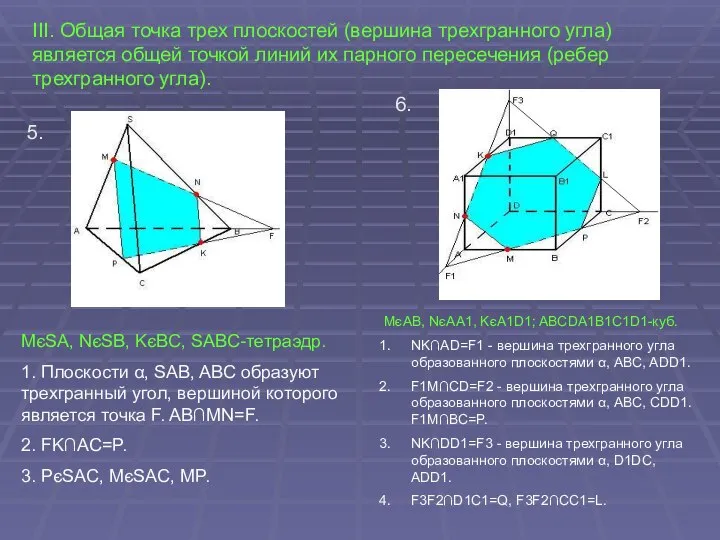
MєSAC, KєABC, NєSBC; SABC-тетраэдр.
Вспомогательная плоскость SMN: SMN∩ABC=M1N1, MN∩M1N1=F, MN∩ABC=F, F- вершина трехгранного угла образованного плоскостями: α, ABC, SMN.
KF∩BC=Q, KF∩AC=L, LM∩SA=R, QN∩SB=P.

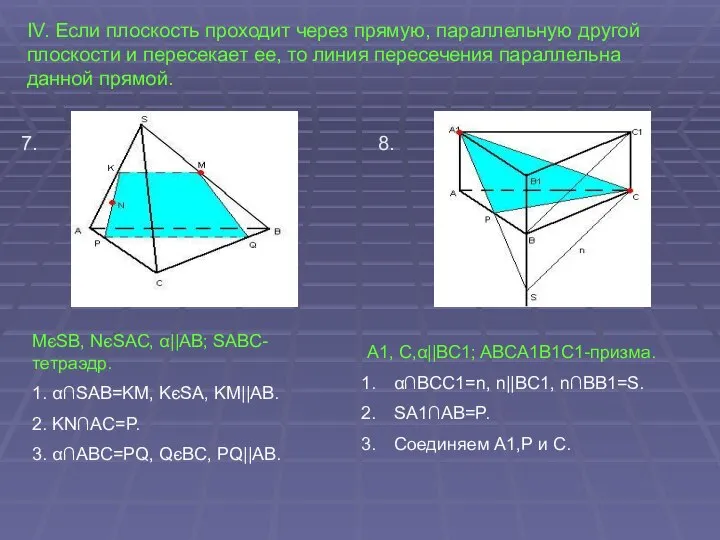
MєA1B1C1, KєBCC1, NєABC; ABCDA1B1C1-параллелепипед.
1. Вспомогательная плоскость MKK1: MKK1∩ABC=M1K1, MK∩M1K1=S, MK∩ABC=S, S- вершина трехгранного угла образованного плоскостями: α, ABC, MKK1.
2. SN∩BC=P, SN∩AD=Q, PK∩B1C1=R, RM∩A1D1=L.

сечения (если да, то через них можно провести сторону сечения).
Построить след сечения на плоскости основания многогранника.
Найти дополнительную точку сечения на ребре многогранника (продолжить сторону основания той грани, в которой есть точка сечения, до пересечения со следом).
Через полученную дополнительную точку на следе и точку сечения в выбранной грани провести прямую, отметить точки пересечения её с рёбрами грани.
Выполнить п.1.

в плоскости основания:
- RQ∩R1Q1=T2, RP∩R1P1=T1.
3. Найдём дополнительную точку:
- Qє(AME), AE∩T1T2=S1.
4. Проведем прямую S1Q
- S1Q∩AM=K, S1Q∩ME=L.
5. KP∩BM=F, LR∩MD=G.
6. Найдём дополнительную точку:
- Fє(BMC), BC∩T1T2=S2.
7. Проведем прямую S2F
- S2F∩CM=N.
8. Соединяем N и G.

Построить сечение плоскостью α, проходящей через точки P,Q,R; PєABM, QєAEM, RєEDM.