Содержание
- 2. Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих координат х и у.
- 3. Окружность Окружностью называетсяся множество точек плоскости, равноудаленных от одной и той же точки плоскости, называемой центром
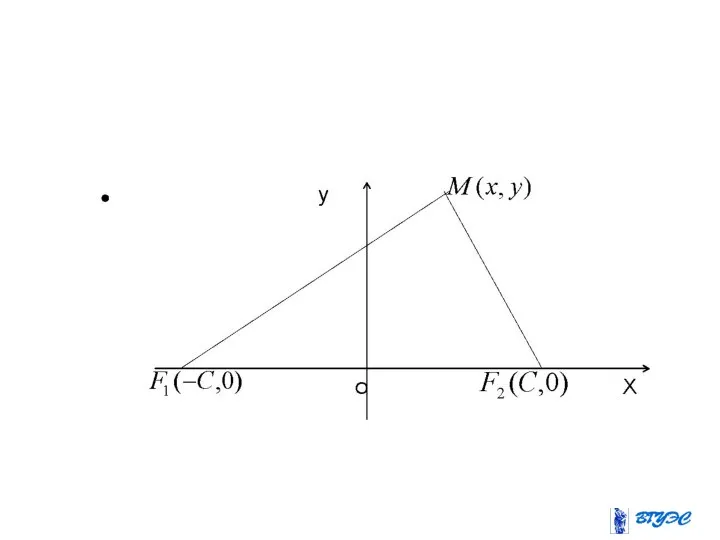
- 4. Эллипс Эллипсом называется геометрическое место точек (плоскости), сумма расстояний которых от двух данных точек, называемых фокусами
- 7. Уравнение эллипса
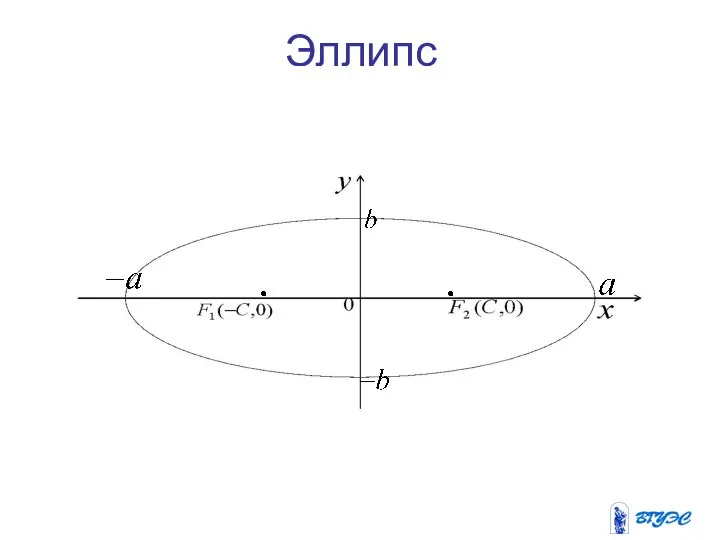
- 8. Эллипс
- 9. Оси симметрии эллипса называются его осями, точка их пересечения- центром эллипса, ось, на которой находятся фокусы
- 10. Точки пересечения эллипса с осями координат называются вершинами эллипса. Это точки с координатами Числа называются полуосями
- 11. Отношение , называется эксцентриситетом эллипса и характеризует его форму, ничего не говоря о его размерах. Чем
- 12. Замечание Если ,то фокальной осью является Фокусы :
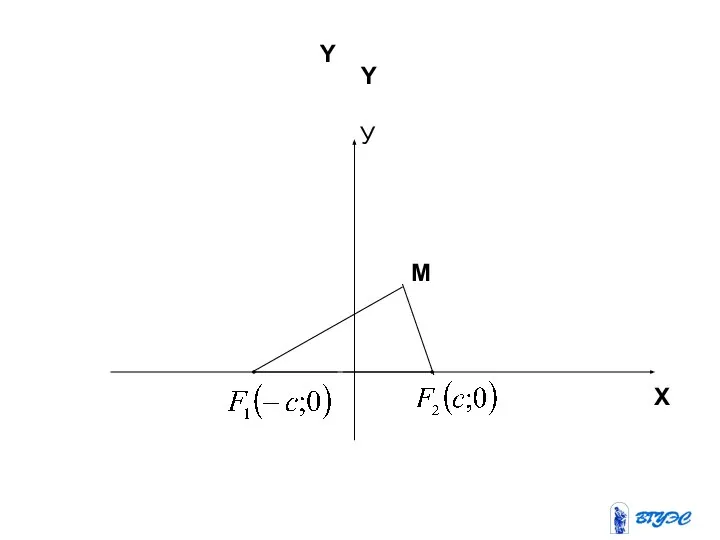
- 13. Гипербола Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек плоскости, называемых фокусами,
- 14. X Y Y M У
- 15. Уравнение гиперболы
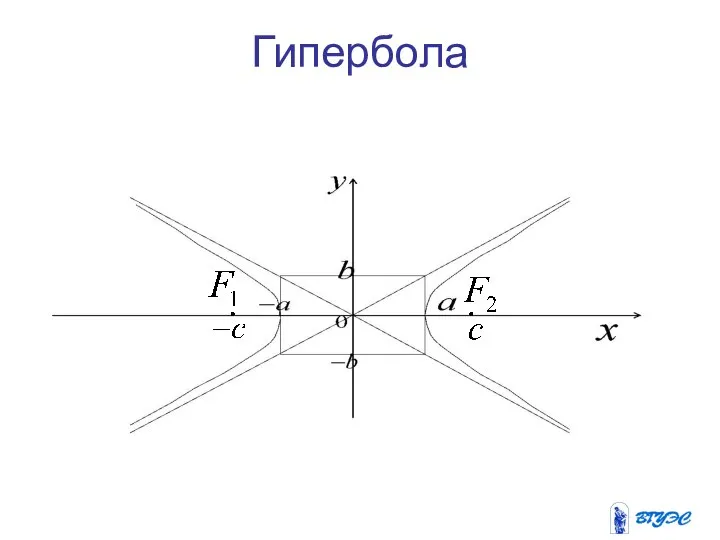
- 16. Гипербола
- 17. Из уравнения гиперболы видно, что точек пересечения с осью Оу нет. Ось Ох называют действительной осью,
- 18. Основной прямоугольник гиперболы Прямоугольник, проходящий через точки со сторонами, параллельными осям координат, называется основным прямоугольником гиперболы.
- 19. Для гиперболы Фокусы гиперболы :
- 20. Оси и полуоси гиперболы Принято говорить: и - действительная и мнимая оси и - действительная и
- 21. Асимптоты Гипербола имеет две асимптоты, т. е. прямые, к которым приближаются точки этой кривой при неограниченном
- 22. Отношение называется эксцентриситетом гиперболы и является мерой ее «сплюснутости», т. е. чем меньше эксцентриситет, тем меньше
- 23. Замечание Для гиперболы -мнимая ось ,а -действительная ось
- 24. Парабола Параболой называется геометрическое место точек, равноудаленных от данной точки плоскости, называемой фокусом, и данной прямой,
- 25. Если расположить ось Ох перпендикулярно директрисе и провести ее через фокус в направлении от директрисы к
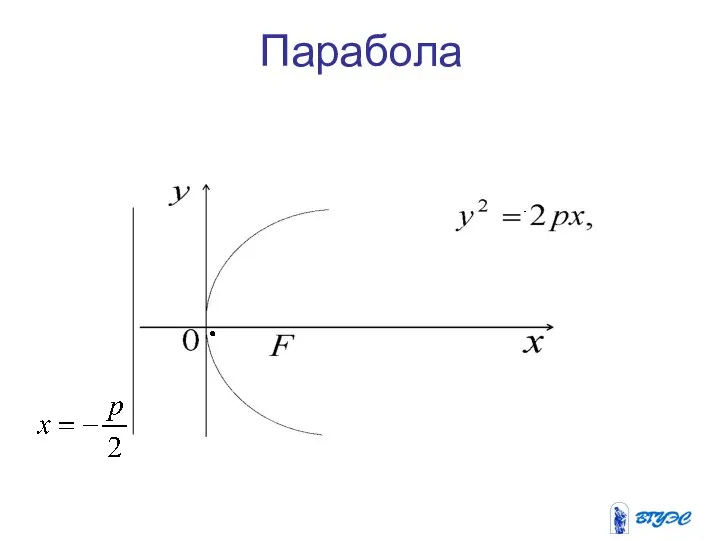
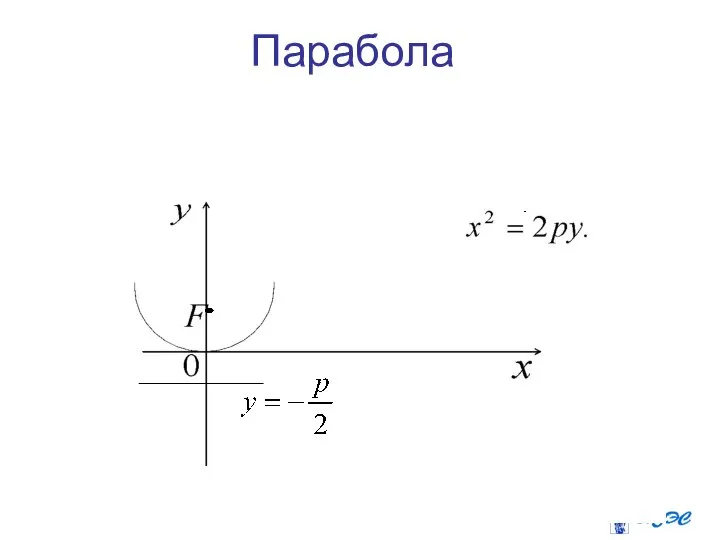
- 26. Парабола
- 27. Фокус параболы - , вершина параболы – в точке директриса параболы это прямая
- 28. Парабола
- 29. Фокус этой параболы вершина такой параболы находится в точке , директриса параболы- это прямая
- 30. Самостоятельно изучить параболы
- 31. Общее уравнение кривой второго порядка Уравнение кривой второго порядка может иметь вид В простейшем случае при
- 32. Пример Привести уравнение 2х²+3у²-16х-64=0 кривой второго порядка к каноническому виду и найти ее центр, полуоси, эксцентриситет,
- 33. Для того чтобы привести уравнение кривой к каноническому виду, выделим полный квадрат переменной х. Для этого
- 34. Это каноническое уравнение эллипса. Полуоси этого эллипса соответственно равны: . Центр эллипса находится в точке С(4;0).
- 35. Пример Составить каноническое уравнение гиперболы, зная, что расстояние между ее фокусами равно 26, а эксцентриситет равен
- 36. Тогда малая полуось Уравнение гиперболы имеет вид
- 37. Пример Составить уравнение гиперболы, если расстояние между вершинами ее равно 20, а расстояние между фокусами равно
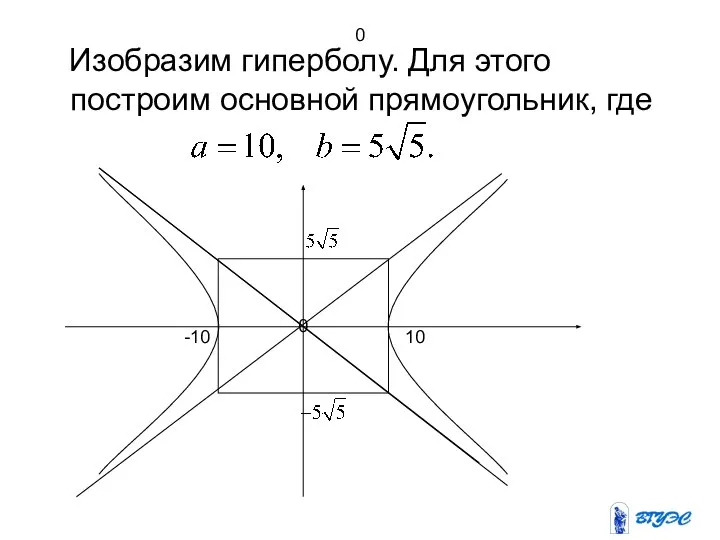
- 38. 0 Изобразим гиперболу. Для этого построим основной прямоугольник, где 0 -10 10
- 40. Скачать презентацию



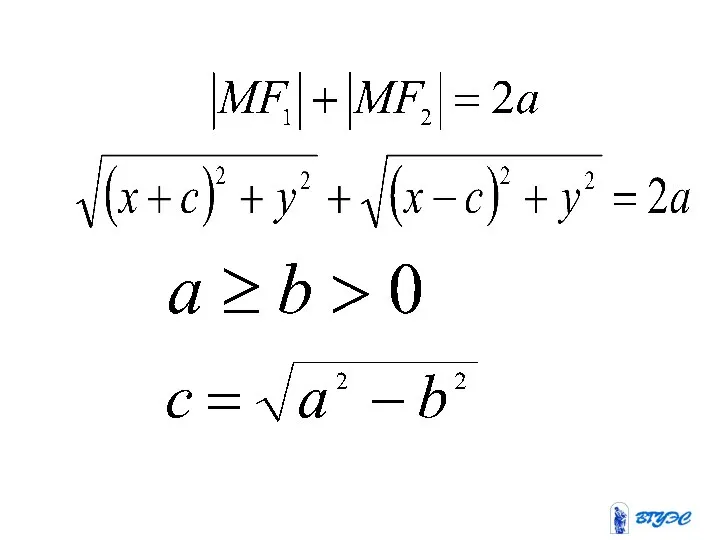
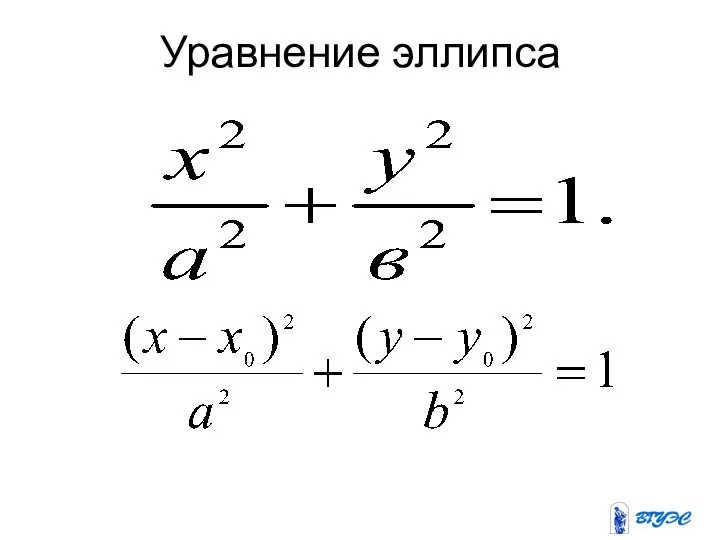








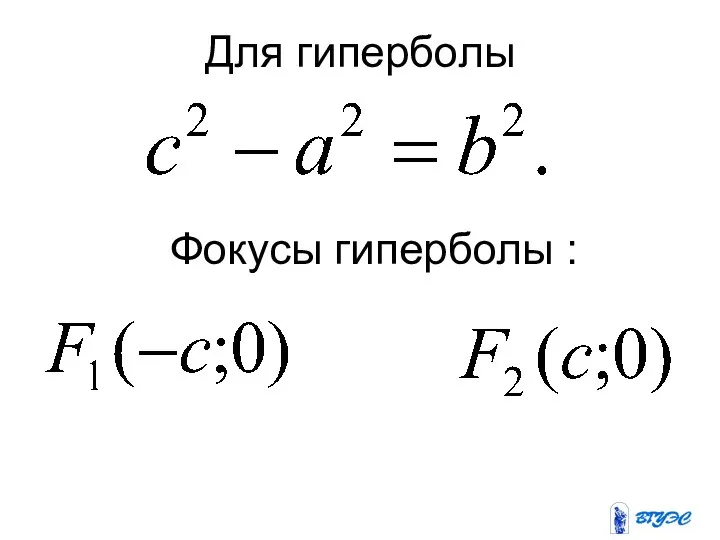
















 Состав числа 4
Состав числа 4 Векторы. Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторов
Векторы. Разложение вектора по направлениям. Координаты вектора. Скалярное произведение векторов Сказочная страна функций. Электронный урок
Сказочная страна функций. Электронный урок Занимательный мир задач
Занимательный мир задач Теория предикатов. Операции над предикатами
Теория предикатов. Операции над предикатами Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений
Математика. Лекция 2. Ранг матрицы. Системы линейных уравнений Вероятностные модели для расчёта надёжности
Вероятностные модели для расчёта надёжности Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск
Решение алгебраических уравнений Выполнил: Нелюбин Алексей 9 «В» класс Школа№3 г. Свирск  Площадь криволинейной трапеции и интеграл
Площадь криволинейной трапеции и интеграл Основні закони логіки висловлювань
Основні закони логіки висловлювань Розв’язування задач за допомогою рівнянь
Розв’язування задач за допомогою рівнянь Логарифмические уравнения. Основные методы их решения. Работу выполнила Курылева Э. Р., учитель математики МОУ «СОШ № 42» г. В
Логарифмические уравнения. Основные методы их решения. Работу выполнила Курылева Э. Р., учитель математики МОУ «СОШ № 42» г. В Презентация на тему Взаимное расположение графиков линейных функций. 7 класс.
Презентация на тему Взаимное расположение графиков линейных функций. 7 класс.  Синус и косинус суммы и разности аргументов
Синус и косинус суммы и разности аргументов Решение систем линейных уравнений
Решение систем линейных уравнений Презентация по математике "ЛИТР (1 КЛАСС)" - скачать бесплатно
Презентация по математике "ЛИТР (1 КЛАСС)" - скачать бесплатно Проценты Ставропольский край Красногвардейский район Поселок Коммунар МОУ СОШ №3 Учитель Ломакина Наталья Викторовна
Проценты Ставропольский край Красногвардейский район Поселок Коммунар МОУ СОШ №3 Учитель Ломакина Наталья Викторовна Таблиця множення числа 4
Таблиця множення числа 4 Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника Вписанная и описанная окружности
Вписанная и описанная окружности Математика-это язык на котором говорят все точные науки Н.И.Лобачевский Нужна ли в жизни координатная плоскость? Авт
Математика-это язык на котором говорят все точные науки Н.И.Лобачевский Нужна ли в жизни координатная плоскость? Авт Параллелограмм и его свойства
Параллелограмм и его свойства Урок математики в 5 классе по теме: «Числовые и буквенные выражения. Уравнения» Учитель математики Левшина Мария Александровна
Урок математики в 5 классе по теме: «Числовые и буквенные выражения. Уравнения» Учитель математики Левшина Мария Александровна Исследование функций
Исследование функций Параллельность прямой и плоскости. Решение задач
Параллельность прямой и плоскости. Решение задач Теория расписаний. Минимизация приоритето-порождающих функций
Теория расписаний. Минимизация приоритето-порождающих функций Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью
Методы решения задач повышенной сложности по геометрии (ЕГЭ). Семинар с практической частью