Содержание
- 2. Замечание Понятия «больше», «меньше» для комплексных чисел не определяются. Записи , и им подобные лишены всякого
- 3. Формула сложения комплексных чисел в новых обозначениях записывается так: . (1) Она дает правило сложения комплексных
- 4. Умножение комплексных чисел, заданных в алгебраической форме, производится следующим образом: . (2)
- 5. Положив в этой формуле , , получим важное соотношение
- 6. или, применяя для произведения сокращенное обозначение , имеем: .
- 7. Пример 1. Найти сумму и произведение комплексных чисел и . Решение. , .
- 8. Определение 1. Комплексное число называется сопряженным к числу и обозначается .
- 9. Утверждение. Для любых комплексных чисел имеют место равенства: 1) , 2) , 3) , 4) .
- 10. Деление комплексных чисел в алгебраической форме производится согласно следующей формуле: .
- 11. Произведем преобразование другим способом. Умножим числитель и знаменатель на , получим:
- 12. Другими словами, чтобы найти частное двух комплексных чисел надо числитель и знаменатель умножить на число, сопряженное
- 13. Геометрическая интерпретация комплексных чисел. Возьмем на плоскости декартову систему координат XOY и изобразим комплексное число точкой
- 14. В итоге комплексному числу будет сопоставлена точка М плоскости. Соответствие между комплексными числами и точками координатной
- 15. Определение 2. Расстояние от точки О координатной плоскости XOY до точки М, изображающей комплексное число ,
- 16. Определение 2. Наименьший угол, на который нужно повернуть ось ОХ против часовой стрелки до совпадения ее
- 17. Определение 2. Непосредственно из рисунка видно, что модуль числа находится по формуле:
- 18. Аргумент числа определяется из формулы при ;
- 19. определяется неоднозначно, а с точностью до слагаемого, кратного : , где есть главное значение , определяемое
- 21. φ Из изображения комплексного числа следует, что , , и, следовательно, .
- 22. Запись комплексного числа в виде называется тригонометрической формой комплексного числа.
- 23. Теорема Для любых комплексных чисел и справедливы равенства: 1) ; 2) .
- 24. Теорема Если , то справедливо равенство: 3) . Доказательство равенств провести в качестве упражнений.
- 25. Формула называется формулой Муавра в честь английского математика А. де Муавра (1667 – 1754).
- 26. Наряду с этой формулой им же была выведена и формула извлечения корня степени из комплексного числа
- 27. Пусть возведем обе части равенства в степень n и, воспользовавшись, формулой Муавра получим: .
- 28. В силу равенства двух комплексных чисел получаем равенства: и или и
- 29. где k – некоторое целое число, - арифметический корень из действительного неотрицательного числа r.
- 30. Таким образом, , причем .
- 31. Пример. Найти все значения корня . Имеем в тригонометрической форме число Согласно формуле , .
- 32. Получим три значения: ; ; .
- 33. Переведем комплексное число, записанное в тригонометрической форме в алгебраическую форму. ;
- 34. ; ; ; ; .
- 35. Поэтому
- 36. Применение формулы Муавра к преобразованиям тригонометрических выражений.
- 37. Пример Выразить через Имеем соотношение
- 38. Возведя правую часть в 5-ую степень, получим
- 39. пользуемся тем, что
- 40. Из равенства чисел, получим
- 41. откуда мы поделили числитель и знаменатель на
- 43. Скачать презентацию



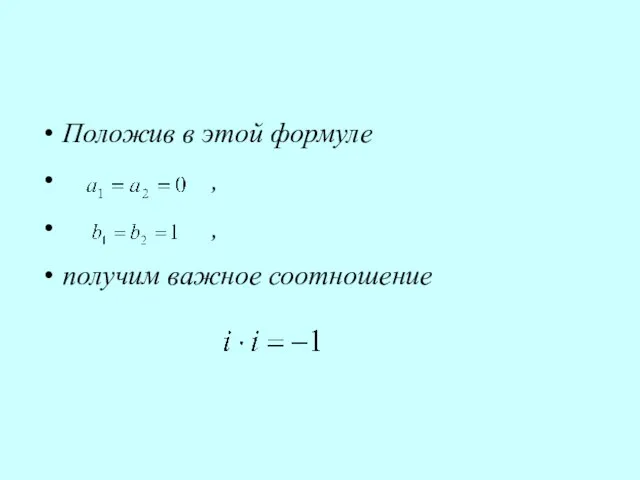














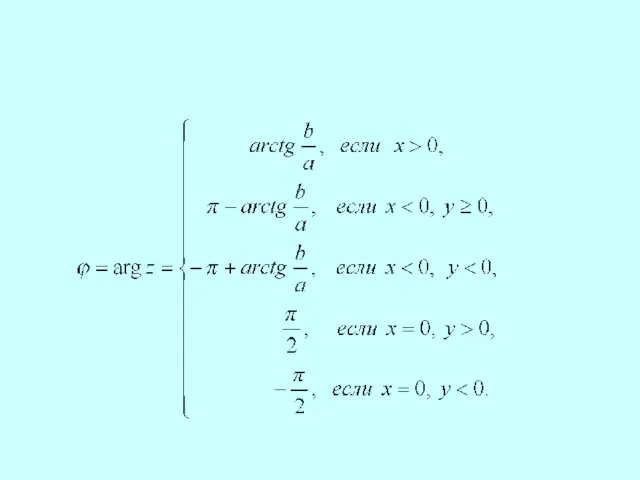













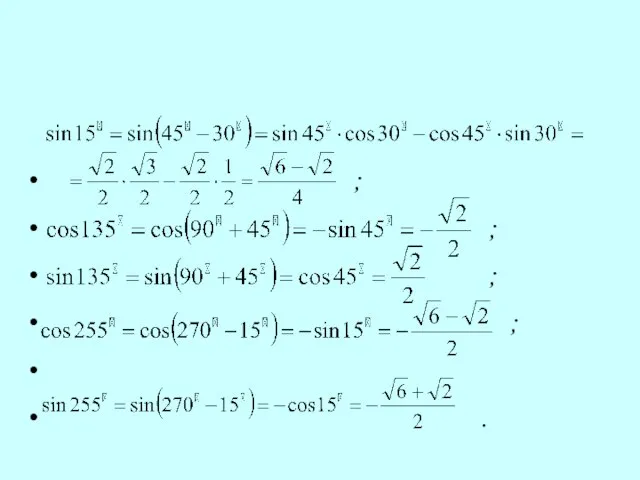




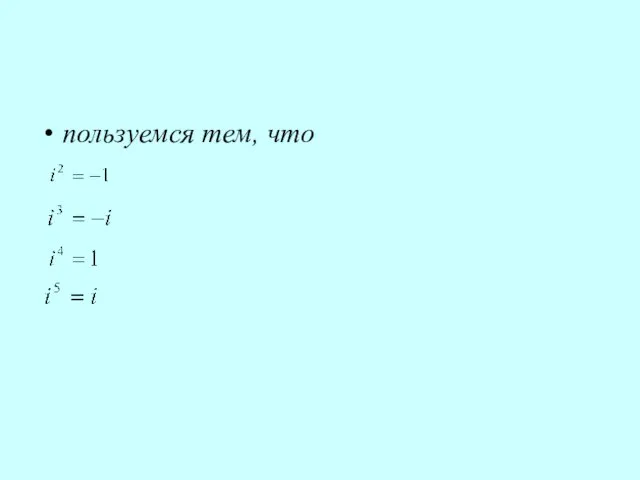


 Презентация на тему Точки и линии. Прямая
Презентация на тему Точки и линии. Прямая  Волшебные часы
Волшебные часы Системы счисления в заданиях ОГЭ и ЕГЭ 2016
Системы счисления в заданиях ОГЭ и ЕГЭ 2016 Сфера
Сфера Площадь кругового сектора
Площадь кругового сектора Как люди считали в старину и как писали цифры
Как люди считали в старину и как писали цифры Решение задач по математике
Решение задач по математике Методические особенности школьного курса математики. (5-6 класс)
Методические особенности школьного курса математики. (5-6 класс) Функции. Способы задания функции
Функции. Способы задания функции Туындының анықтамасы
Туындының анықтамасы Понятие доли. Нахождение одной доли от целого
Понятие доли. Нахождение одной доли от целого Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева)
Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева) Аттестационная работа. Образовательная программа элективного курса. Математика - абитуриенту. (11 класс)
Аттестационная работа. Образовательная программа элективного курса. Математика - абитуриенту. (11 класс) Презентация на тему Дискретный анализ Комбинаторика. Перестановки
Презентация на тему Дискретный анализ Комбинаторика. Перестановки  Взаимно обратные функции
Взаимно обратные функции Синус, косинус и тангенс углов от 0⁰ до 180 ⁰
Синус, косинус и тангенс углов от 0⁰ до 180 ⁰ Вписанная и описанная призмы. Задания
Вписанная и описанная призмы. Задания Математика 1 класс. Ломаные линии. Звено ломаной линии. Вершины
Математика 1 класс. Ломаные линии. Звено ломаной линии. Вершины Презентация по математике "Галерея великих" - скачать
Презентация по математике "Галерея великих" - скачать  УРОК МАТЕМАТИКИ В 4 А КЛАССЕ Составление примеров на деление. Линии. Попикова Наталья Александровна, учитель начальных класс
УРОК МАТЕМАТИКИ В 4 А КЛАССЕ Составление примеров на деление. Линии. Попикова Наталья Александровна, учитель начальных класс Тригонометрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень)
Тригонометрия (по материалам открытого банка задач ЕГЭ по математике (профильный уровень) Первообразная
Первообразная Преобразование выражений, содержащих радикалы
Преобразование выражений, содержащих радикалы Элементы теории множеств при работе с информацией
Элементы теории множеств при работе с информацией Наглядная геометрия. 5-6 классы
Наглядная геометрия. 5-6 классы Понятие функции
Понятие функции Интервальное оценивание параметров ( лекция 7)
Интервальное оценивание параметров ( лекция 7) Формула корней квадратного уравнения
Формула корней квадратного уравнения