Содержание
- 2. Число е. Функция y = ex, её свойства, график, дифференцирование
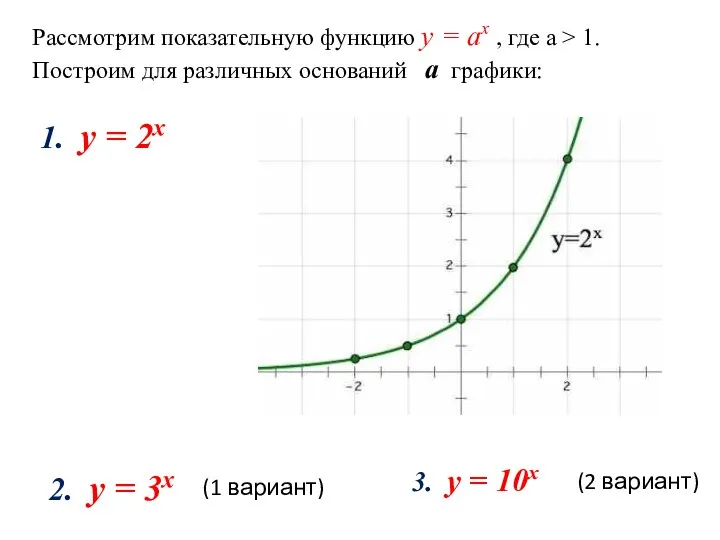
- 3. Рассмотрим показательную функцию y = аx , где а > 1. Построим для различных оснований а
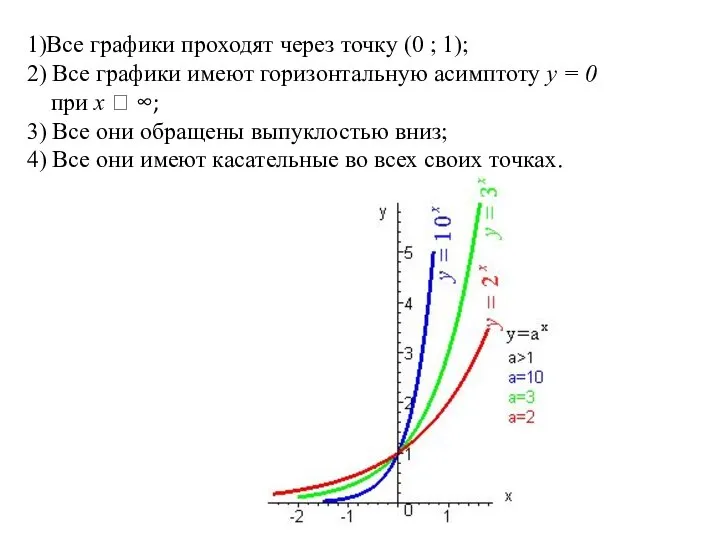
- 4. 1)Все графики проходят через точку (0 ; 1); 2) Все графики имеют горизонтальную асимптоту у =
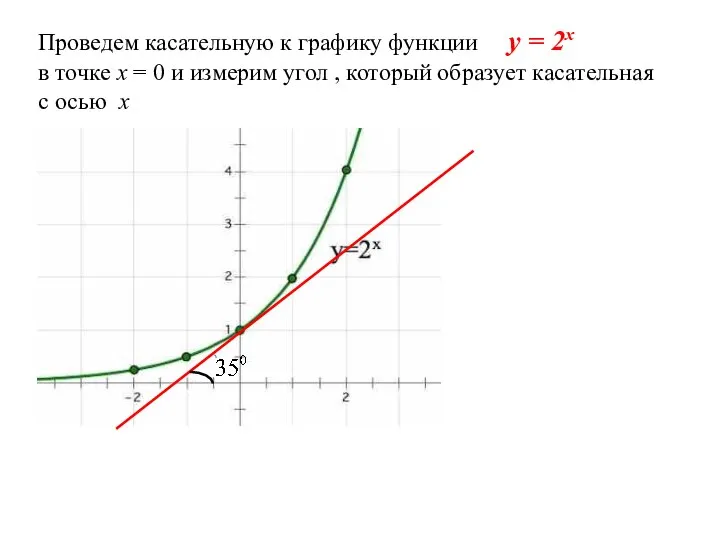
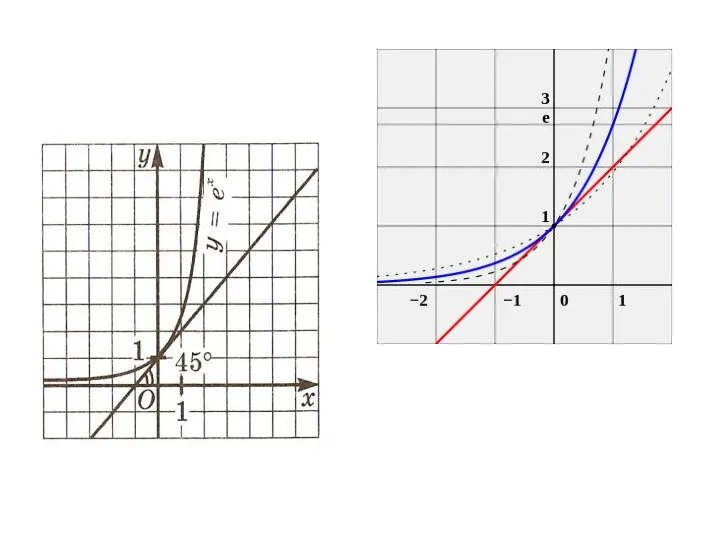
- 5. Проведем касательную к графику функции y = 2x в точке х = 0 и измерим угол
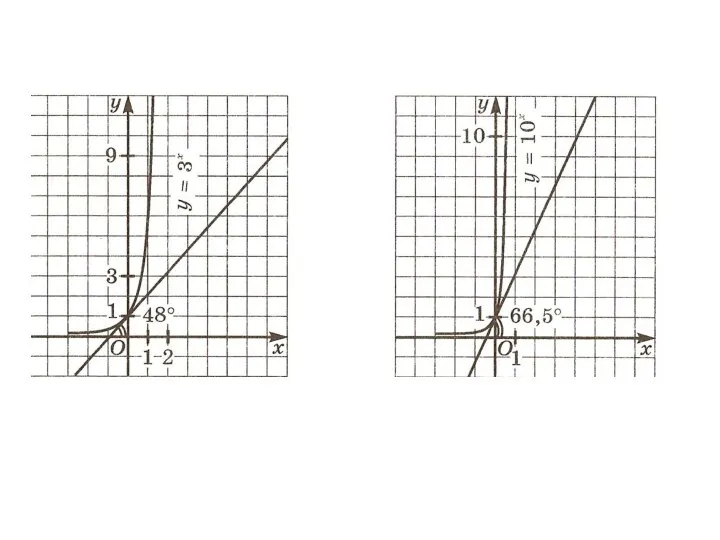
- 7. С помощью точных построений касательных к графикам можно заметить, что если основание а показательной функции y
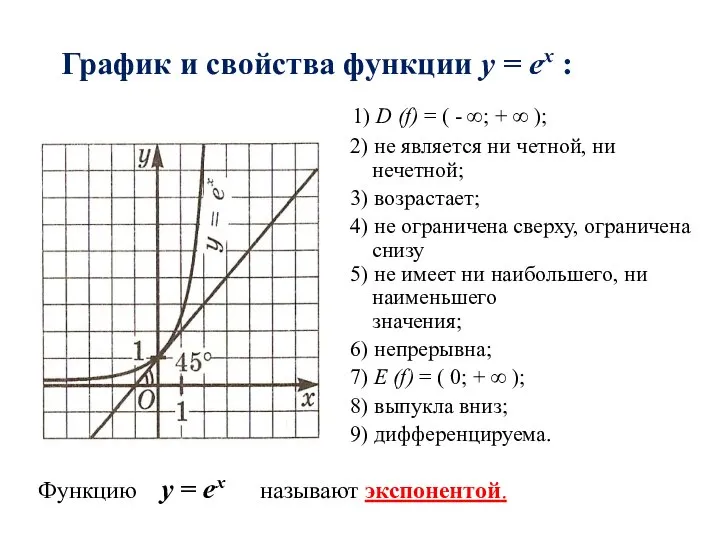
- 9. График и свойства функции y = еx : 1) D (f) = ( - ∞; +
- 10. В курсе математического анализа доказано, что функция y = еx имеет производную в любой точке х:
- 11. Пример 1. Провести касательную к графику функции в точке x=1. Решение: 1) =1 2) f( )=f(1)=e
- 12. Пример 2. Вычислить значение производной функции в точке x = 3. Решение: Ответ: 4
- 13. Пример 3. Исследовать на экстремум функцию Решение: 1) 2) х=0 и х=-2
- 14. 3) -2 x 0 + + - 4) х = -2 – точка максимума х =
- 15. Натуральные логарифмы. Функция y = ln x, её свойства, график, дифференцирование
- 16. Если основанием логарифма служит число е, то говорят, что задан натуральный логарифм. Для натуральных логарифмов введено
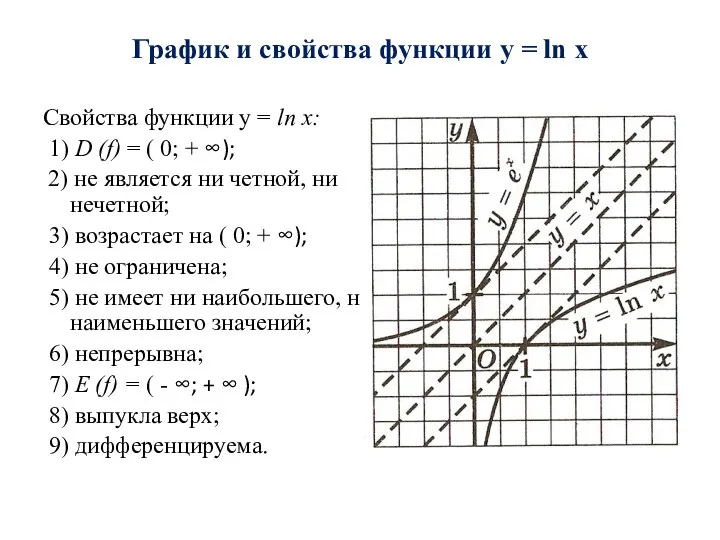
- 17. Свойства функции y = ln x: 1) D (f) = ( 0; + ∞); 2) не
- 18. В курсе математического анализа доказано, что для любого значения х>0 справедлива формула дифференцирования
- 19. Вычислить значение производной функции в точке x = -1. Пример 4: Решение: Ответ: 1,5
- 20. Дифференцирование функции Например:
- 21. Дифференцирование функции
- 24. Скачать презентацию













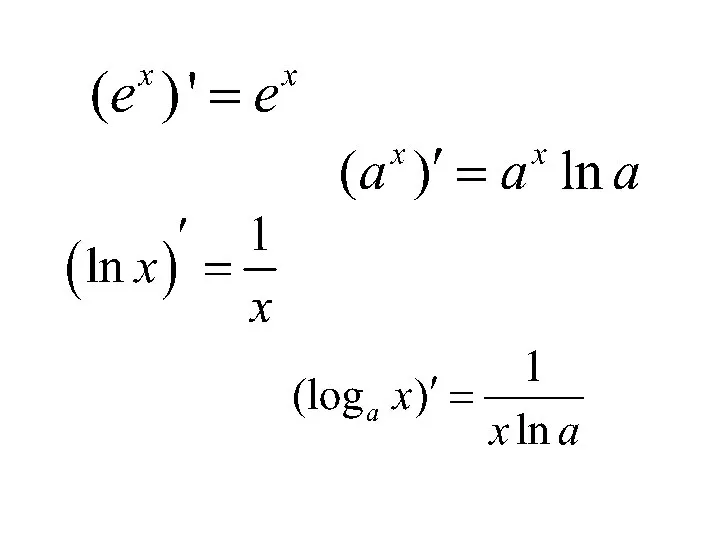
 Сумма углов треугольника
Сумма углов треугольника Figures of matching
Figures of matching Аттестационная работа. Подготовка к итоговой аттестации по математике в новой форме. (9 класс)
Аттестационная работа. Подготовка к итоговой аттестации по математике в новой форме. (9 класс) Великая теорема Ферма
Великая теорема Ферма Построение графика функци y= x
Построение графика функци y= x Формы графического изображения. (Лекция 3)
Формы графического изображения. (Лекция 3) Косинус угла
Косинус угла Поворот и параллельный перенос
Поворот и параллельный перенос Дифференциальные уравнения 2-го порядка Лекция 5
Дифференциальные уравнения 2-го порядка Лекция 5  Основы теории логических преобразований
Основы теории логических преобразований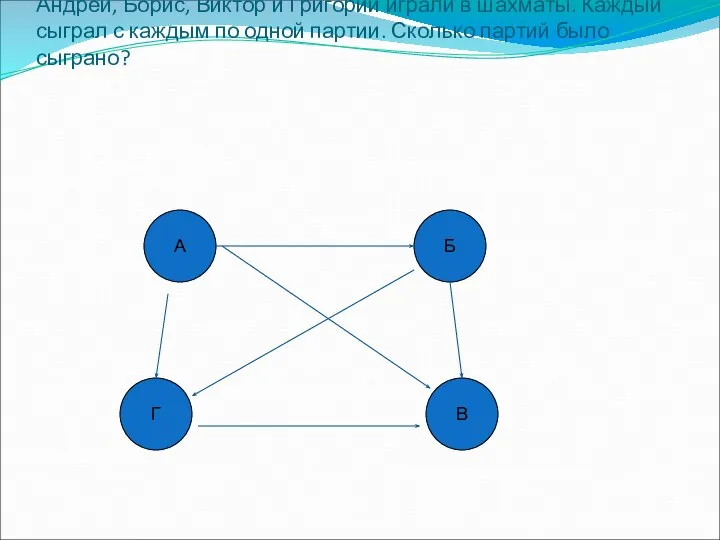 Решение задач с помощью графов
Решение задач с помощью графов Раскрытие скобок
Раскрытие скобок Иррациональные уравнения
Иррациональные уравнения Математика «Четырехзначные числа» «Величины» «Умножение в пределах 100» 3 класс Н.Б.Истомина тесты
Математика «Четырехзначные числа» «Величины» «Умножение в пределах 100» 3 класс Н.Б.Истомина тесты Математический ералаш
Математический ералаш Проценты в жизни человека. 5 класс
Проценты в жизни человека. 5 класс Применение производной к исследованию функции
Применение производной к исследованию функции Кроссворд по геометрии
Кроссворд по геометрии Частные производные функции
Частные производные функции Вписанные и описанные окружности
Вписанные и описанные окружности Мастер-класс Решение задач по геометрии при подготовке к ОГЭ
Мастер-класс Решение задач по геометрии при подготовке к ОГЭ Графики. График движения
Графики. График движения Вынесение множителя из-под знака корня. Внесение множителя под знак корня
Вынесение множителя из-под знака корня. Внесение множителя под знак корня Нахождение свойств производной по графику функции (№7 ЕГЭ)
Нахождение свойств производной по графику функции (№7 ЕГЭ) Линейные дифференциальные уравнения 1-ого порядка
Линейные дифференциальные уравнения 1-ого порядка Задачи. Ломаная линия
Задачи. Ломаная линия Математический вечер Ох, уж эта математика
Математический вечер Ох, уж эта математика Нахождение числа по значению его дроби
Нахождение числа по значению его дроби