Содержание
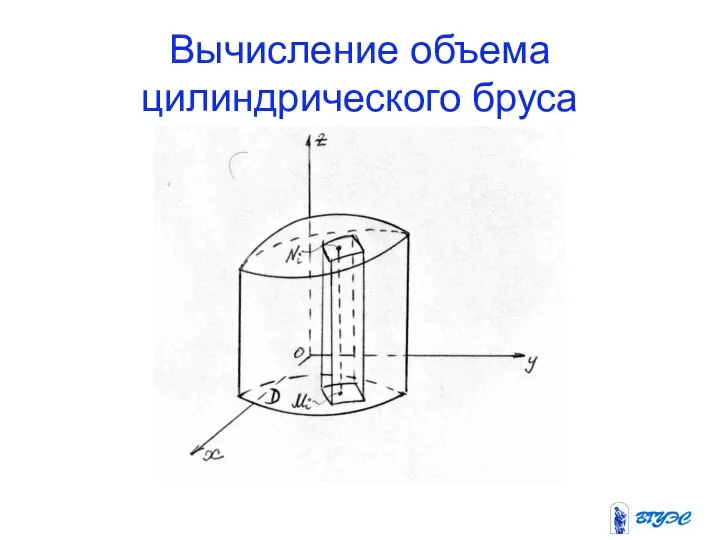
- 2. Цилиндрический брус Назовём цилиндрическим брусом, или цилиндроидом, тело, ограниченное плоскостью Oxy, поверхностью z=f(x,y) и цилиндрической поверхностью,
- 3. Вычисление объема цилиндрического бруса
- 4. Продолжение Объём цилиндра приближённо выражается суммой где Δσi –площадь элементарной ячейки . Таким образом, переходя к
- 5. Определение двойного интеграла Определение. Если существует конечный предел интегральных сумм при условии, что max diam Δσi→0,
- 6. Продолжение Таким образом, по определению = В этой формуле f(x,y) называют подынтегральной функцией, D – областью
- 7. Некоторые определения Назовём область D замкнутой, если этой области принадлежат как внутренние, так и граничные точки
- 8. Некоторые определения Кривая называется гладкой, если эта кривая непрерывна и в каждой точке имеет касательную, непрерывно
- 9. Некоторые определения Кусочно – гладкой мы называем кривую, которую можно разбить на гладкие кривые точками. Например,
- 10. Условие существования двойного интеграла Если область D с кусочно – гладкой границей Г ограничена и замкнута,
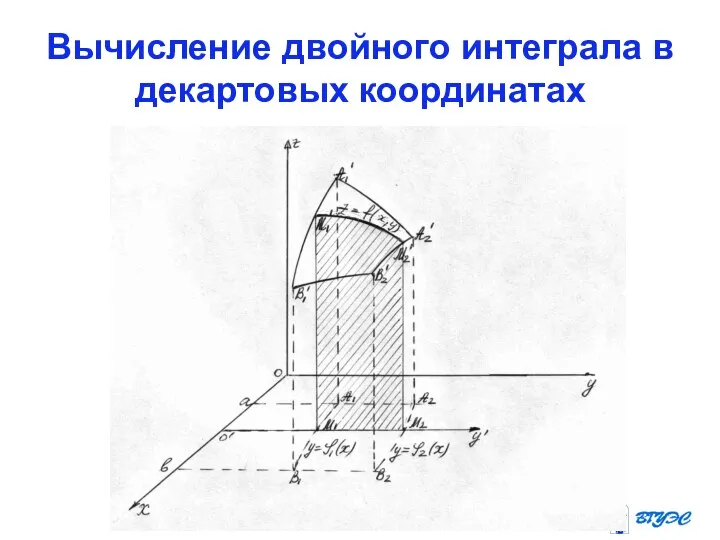
- 11. Двойной интеграл в декартовых координатах Так как двойной интеграл не зависит от способа разбиения области на
- 12. Двойной интеграл в декартовых координатах Тогда имеем =
- 13. Правильная в направлении оси оУ область Пусть область ограничена сверху и снизу кривыми, изображенными на рисунке,
- 14. Двукратный интеграл Назовем двукратным интегралом по области, простой и правильной в направлении оси Ох , интеграл
- 15. Вычисление двойного интеграла в декартовых координатах
- 16. Сведение двойного интеграла к двукратному Двойной интеграл по области, простой и правильной в направлении оси Ох,
- 17. Если область простая и правильная в направлении оси оХ
- 19. Скачать презентацию














 Сопряжение
Сопряжение Раскрытие скобок. Устный счёт
Раскрытие скобок. Устный счёт Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Презентация на тему Единицы массы. Грамм
Презентация на тему Единицы массы. Грамм  Осевая и центральная симметрия
Осевая и центральная симметрия Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Степенная функция
Степенная функция Математическое моделирование: основные понятия и определения
Математическое моделирование: основные понятия и определения Однородные тригонометрические уравнения
Однородные тригонометрические уравнения Прямоугольник (урок № 73)
Прямоугольник (урок № 73) Теорема Пифагора
Теорема Пифагора Конкурс "А ну-ка, математики!"
Конкурс "А ну-ка, математики!" Геометрична фігура трикутник. (7 класс)
Геометрична фігура трикутник. (7 класс) Подготовка к введению задач в 2 действия
Подготовка к введению задач в 2 действия Исследование функции одной переменной
Исследование функции одной переменной Презентация по математике "Математика. Задачи" - скачать
Презентация по математике "Математика. Задачи" - скачать  Задачи в готовых чертежах по теме: «Признаки равенства треугольников»
Задачи в готовых чертежах по теме: «Признаки равенства треугольников» Понятие множества
Понятие множества Исследовательская работа по теме «Арифметика» Л.Ф. Магницкого. Задачи на сплавы и смеси». Выполнила Чистякова Надежда Ученица 8 «В
Исследовательская работа по теме «Арифметика» Л.Ф. Магницкого. Задачи на сплавы и смеси». Выполнила Чистякова Надежда Ученица 8 «В Формализация описания структуры
Формализация описания структуры Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач. Автор: Линдфуйт Наталья, ученица 9 класса Руко
Применение теоремы Пифагора и пифагоровых троек для решения геометрических задач. Автор: Линдфуйт Наталья, ученица 9 класса Руко Математическая статистика
Математическая статистика Правильный октаэдр
Правильный октаэдр Смежные и вертикальные углы. Геометрия. 7 класс
Смежные и вертикальные углы. Геометрия. 7 класс Исследование функции с помощью производной
Исследование функции с помощью производной Аттестационная работа. Программа внеурочной деятельности по математике Почемучки
Аттестационная работа. Программа внеурочной деятельности по математике Почемучки Прямоугольный параллелепипед
Прямоугольный параллелепипед Игра-путешествие по стране «Математика»
Игра-путешествие по стране «Математика»