Содержание
- 2. Основное определение Неориентированный ГРАФ – это упорядоченная пара (V,E), где: V – множество вершин (конечное); E
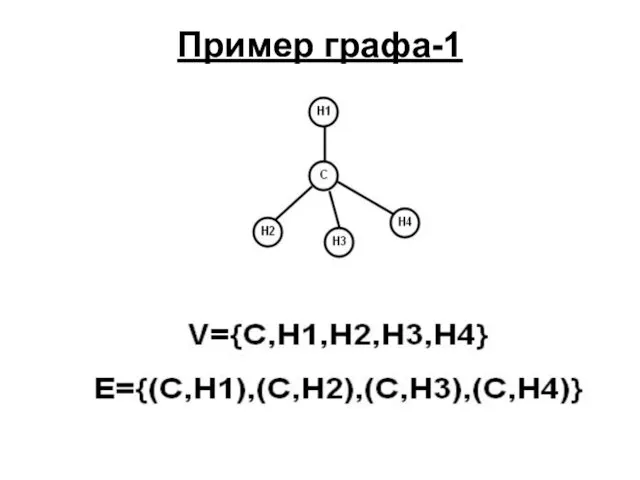
- 3. Пример графа-1
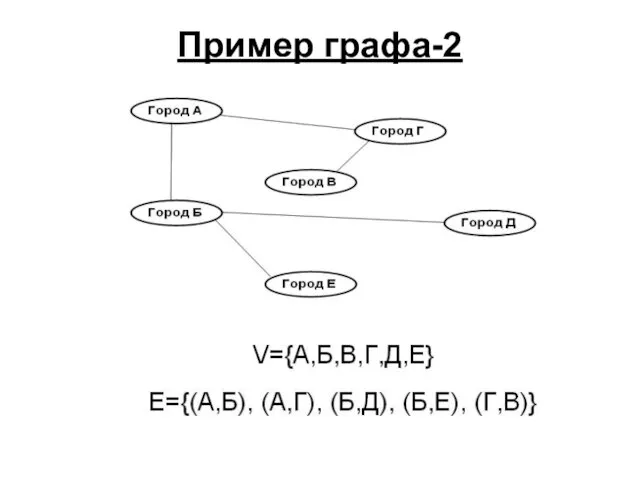
- 4. Пример графа-2
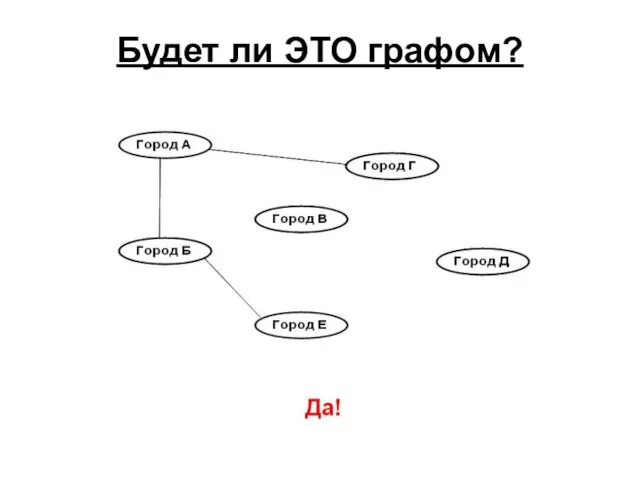
- 5. Будет ли ЭТО графом?
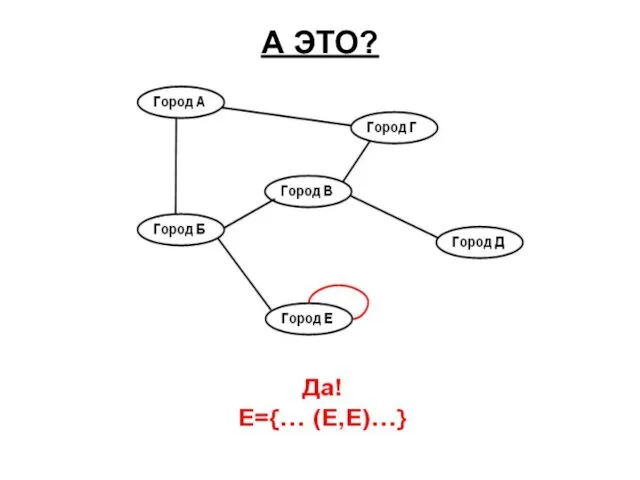
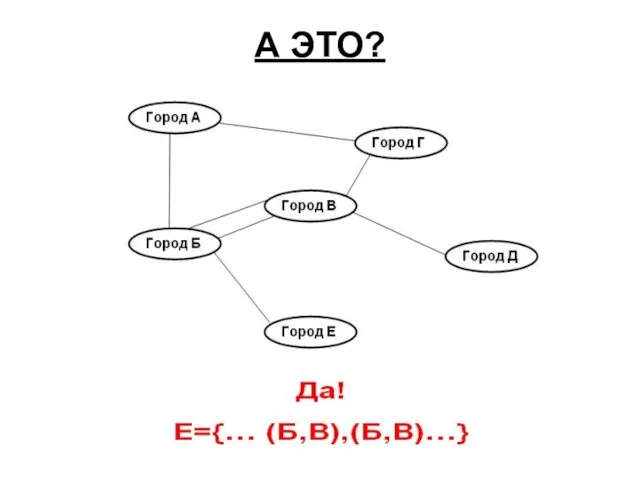
- 6. А ЭТО?
- 7. А ЭТО?
- 8. Порядок и размер графа Количество вершин называется порядком графа. Количество ребер называется размером графа.
- 9. Некоторые термины-1 Пусть R=(a,b) – одно из ребер графа. Тогда вершины a и b называются концевыми
- 10. Степенью вершины V обозначается deg(V) называется количество ребер, для которых эта вершина является концевой; Вершина называется
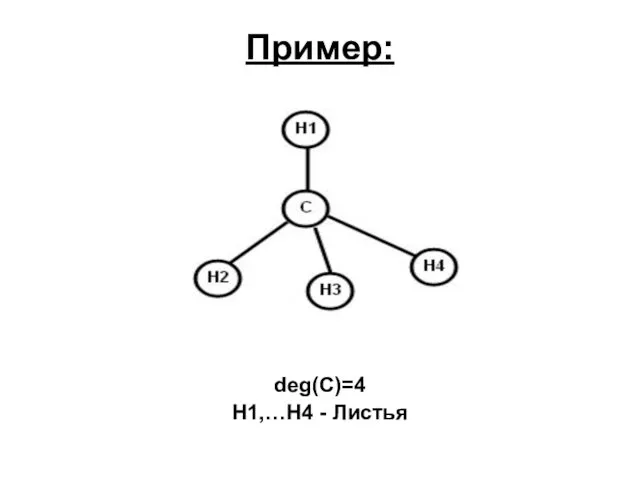
- 11. Пример: deg(C)=4 H1,…H4 - Листья
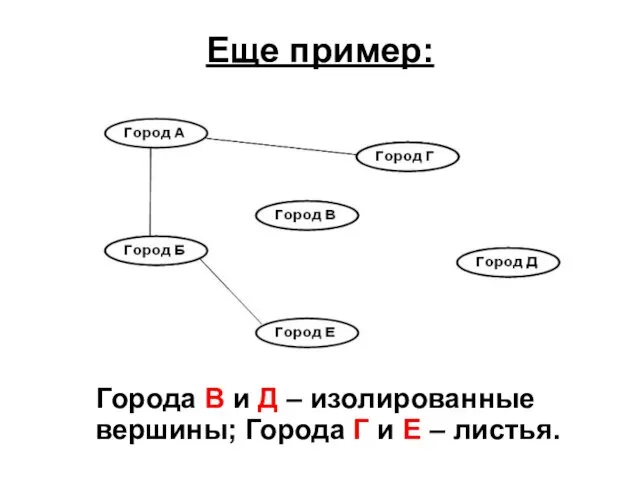
- 12. Еще пример: Города B и Д – изолированные вершины; Города Г и Е – листья.
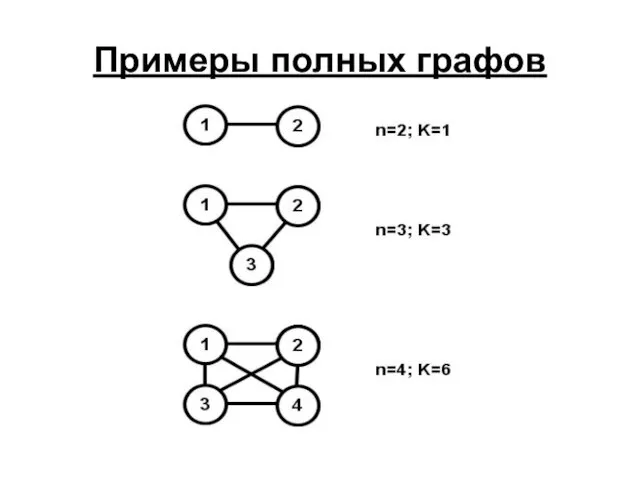
- 13. Полный граф Граф называется полным, если любые две вершины соединены ребром. Сколько ребер у полного графа
- 14. Давайте это докажем… Полный граф с двумя вершинами содержит одно ребро – это очевидно. Подставим n=2
- 15. Предположение индукции Предположим, что формула верна для графа c k вершинами. Докажем, что отсюда следует справедливость
- 16. Добавим к полному графу с K вершинами еще одну вершину. И соединим ее с первыми K
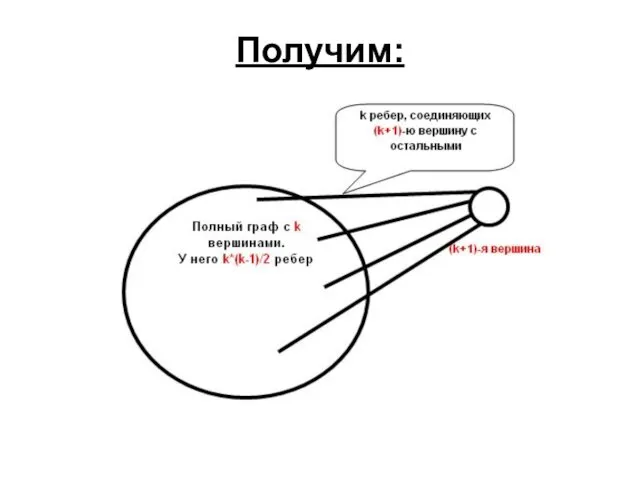
- 17. Получим:
- 18. Считаем, сколько получилось ребер… K*(K-1)/2 + K = K*(K+1)/2 Последнее выражение получается, если в формулу n*(n-1)/2
- 19. Из предположения справедливости утверждения при n=k следует справедливость утверждения при n=k+1. Теорема доказана.
- 20. Примеры полных графов
- 21. Важное уточнение Пары, задающие ребра в неориенти-рованном графе, неупорядочены (т.е. пары (a,b) и (b,a) не различают-ся)
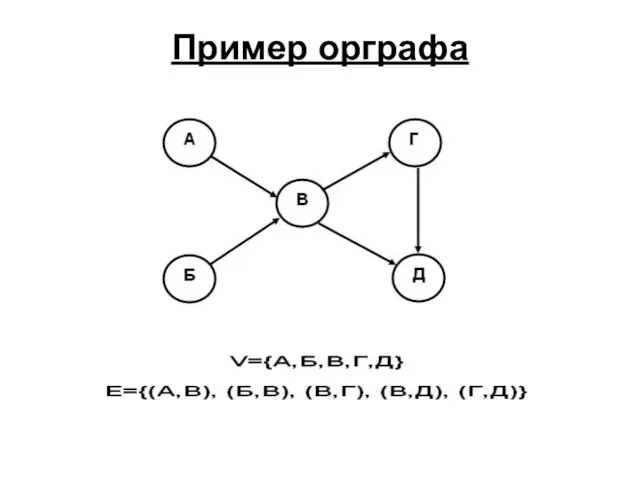
- 22. Ориентированный граф Если ребра графа есть множество упорядоченных пар (т.е. (a,b) ≠ (b,a)), То граф называется
- 23. Пример орграфа
- 24. Смешанный граф Смешанный граф – это тройка (V, E, A). V – множество вершин; E –
- 25. Изоморфизм графов Пусть имеется два графа G1 и G2 Если имеется взаимно-однозначное соответствие F между вершинами
- 26. Уточнение Для орграфов и смешанных графов соответствие F должно сохранять ориентацию дуг.
- 27. Необходимое условия изоморфизма При каких условиях между элементами двух конечных множеств можно установить взаимно-однозначное соответствие? Тогда
- 28. Достаточно ли это условие? Нет, поскольку вершины могут быть соединены по-разному.
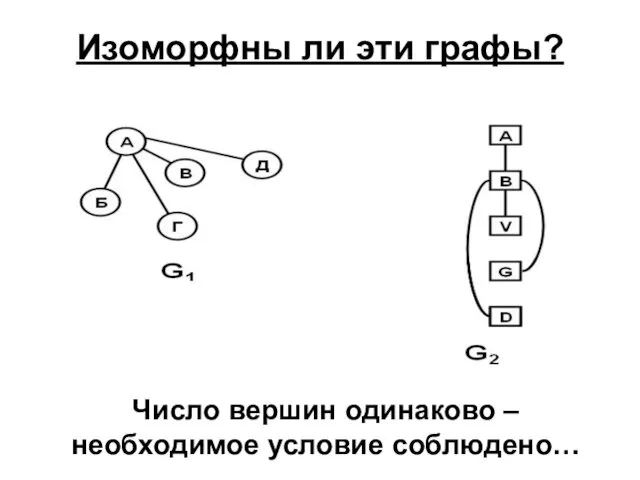
- 29. Изоморфны ли эти графы? Число вершин одинаково – необходимое условие соблюдено…
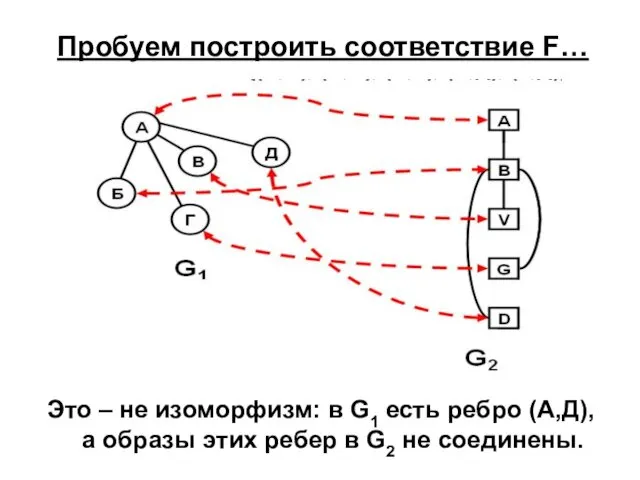
- 30. Пробуем построить соответствие F… Это – не изоморфизм: в G1 есть ребро (A,Д), а образы этих
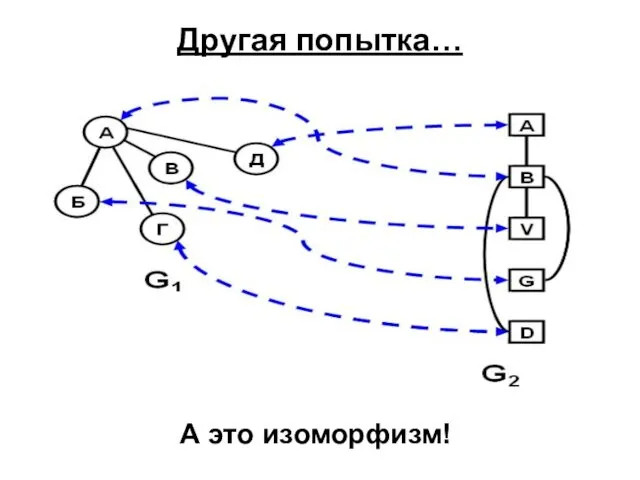
- 31. Другая попытка… А это изоморфизм!
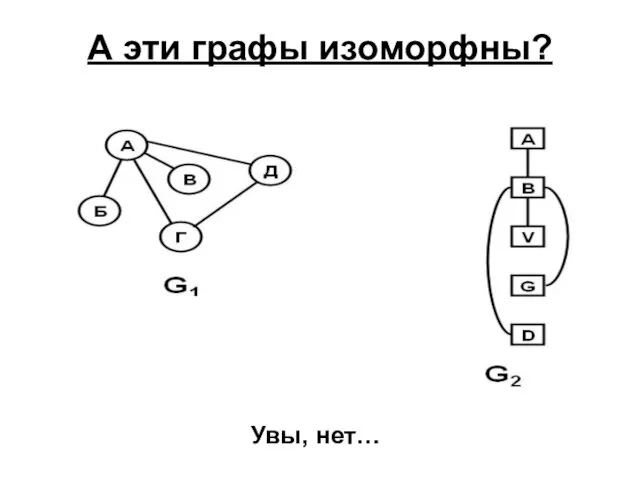
- 32. А эти графы изоморфны? Увы, нет…
- 33. С точки зрения теории два изоморфных графа – это один и тот же объект (только, может
- 34. Пути (цепи): Путь (цепь) это последовательность вершин: a1, a2, … , an в которой соседние вершины
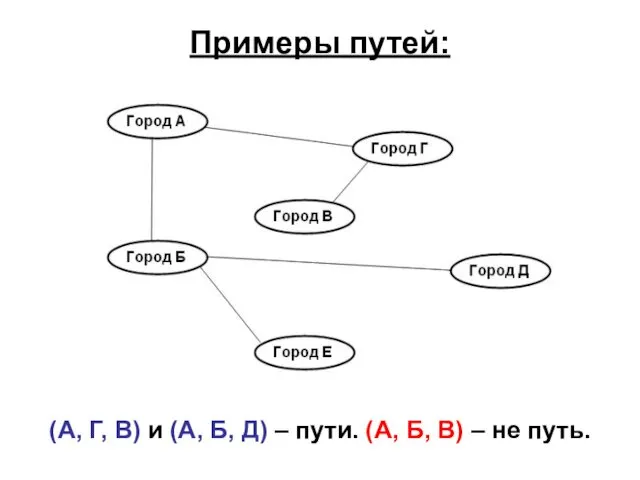
- 35. Примеры путей: (А, Г, В) и (А, Б, Д) – пути. (А, Б, В) – не
- 36. Понятие пути для орграфа сохраняет силу, но нуждается в дополнении – соседние вершины в последовательности a1,
- 37. Циклы Цикл – это путь, у которого начальная и конечная вершина совпадают. Длина цикла есть число
- 38. Компоненты связности Вершины произвольного графа можно разбить на классы, такие, что для любых двух вершин одного
- 39. Машинное представление графов.
- 40. Матрица смежности Занумеруем вершины графа G последовательными целыми от 1 до n; Построим квадратную таблицу n×n
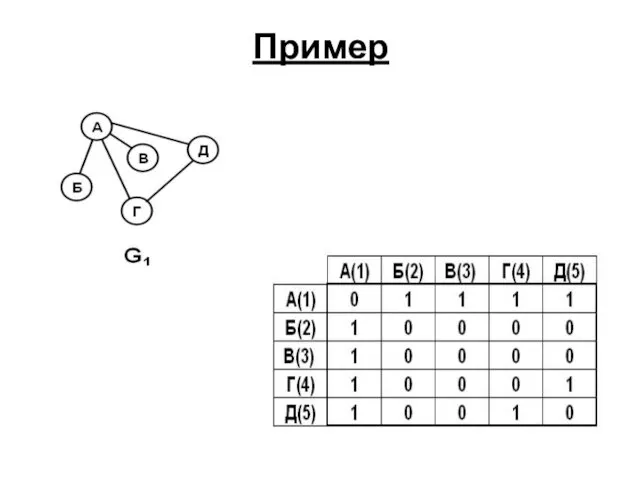
- 41. Пример
- 42. Некоторые очевидные свойства матрицы смежности Если вершина изолирована, то ее строка и столбец будут полностью нулевые;
- 43. Обобщение для орграфа Матрицу смежности для орграфа можно строить аналогичным образом, но, чтобы учесть порядок вершин,
- 44. Матрица инцидентности Занумеруем вершины графа G последовательными целыми от 1 до n; Построим прямоугольную таблицу с
- 45. Матрица инцидентности для орграфа Если j-я дуга исходит из вершины k, то в позиции (k,j) ставится
- 46. Поскольку столбцы матрицы инцидентности описывают ребра, то в каждом столбце может быть не более двух ненулевых
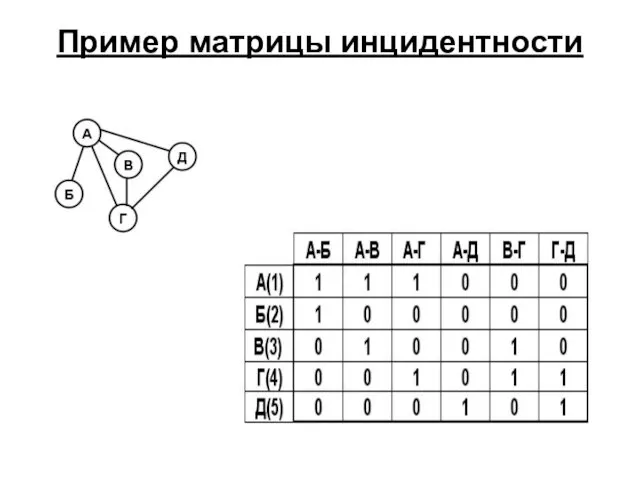
- 47. Пример матрицы инцидентности
- 48. Список ребер Еще один способ представления графа – двумерный массив (список пар). Количество пар равно числу
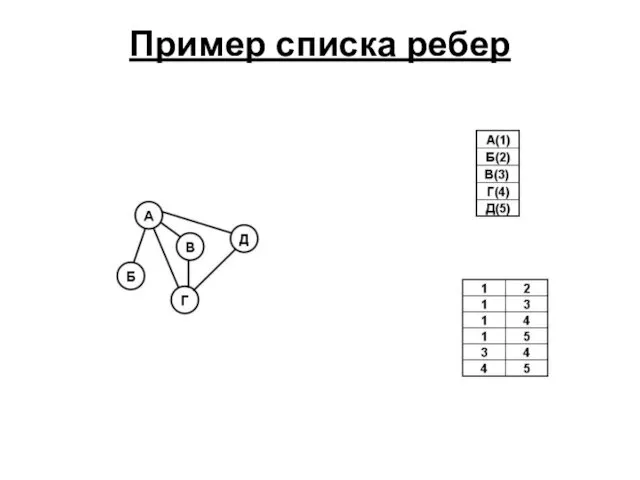
- 49. Пример списка ребер
- 50. Сравнение разных способов представления Список ребер самый компактный, а матрица инцидентности наименее компактна; Матрица инцидентности удобна
- 51. Обход графа Обходом графа называется перебор его вершин, такой, что каждая вершина просматривается один раз.
- 52. Соглашение-1 Перед выполнением поиска для графа с n вершинами заведем массив Chk из n элементов и
- 53. Соглашение-2 Заведем структуру данных (хранилище), в котором будем запоминать вершины в процессе обхода. Интерфейс хранилища должен
- 54. Соглашение-3 Когда вершина j помещается в хранилище, она отмечается как просмотренная (т.е. устанавливается Chk[j]=1)
- 55. Алгоритм обхода-1 1) Берем произвольную начальную вершину, печатаем и заносим ее в хранилище; 2) Хранилище пусто?
- 56. Алгоритм обхода-2 1) Берем произвольную начальную вершину и заносим ее в хранилище; 2) Хранилище пусто? Если
- 57. Какие структуры данных подходят в качестве хранилища? Стек (PUSH – занести; POP – извлечь) Очередь (ENQUE
- 58. Алгоритм-1 в сочетании со стеком называется обходом в глубину Алгоритм-2 в сочетании с очередью называется обходом
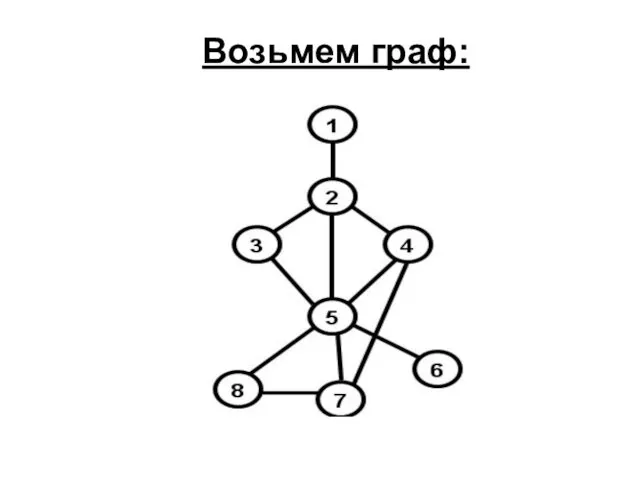
- 59. Возьмем граф:
- 60. В качестве хранилища возьмем СТЕК. Используем Алгоритм-1. Обход начнем с вершины 1
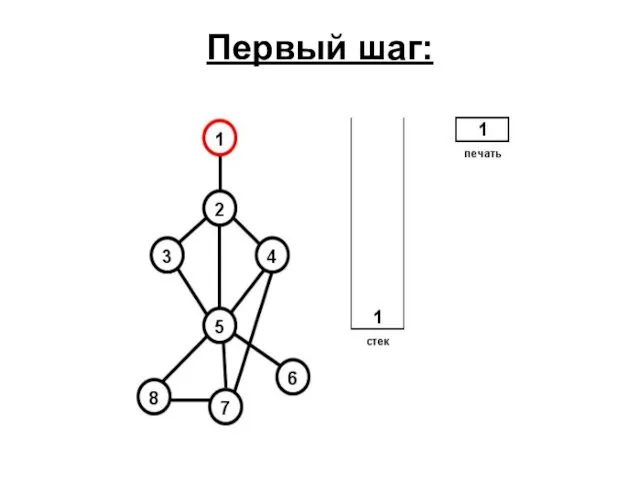
- 61. Первый шаг:
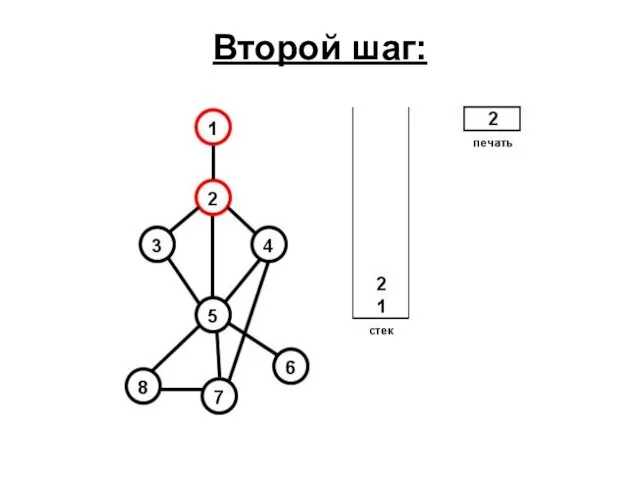
- 62. Второй шаг:
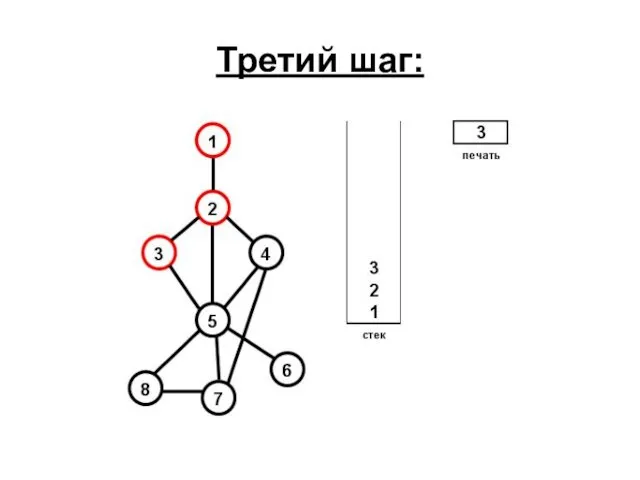
- 63. Третий шаг:
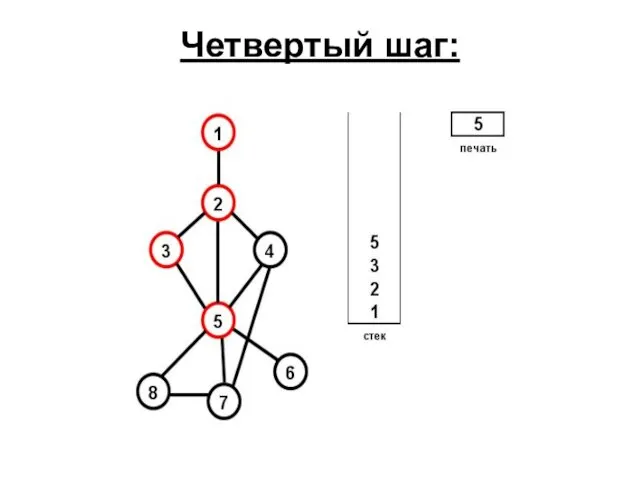
- 64. Четвертый шаг:
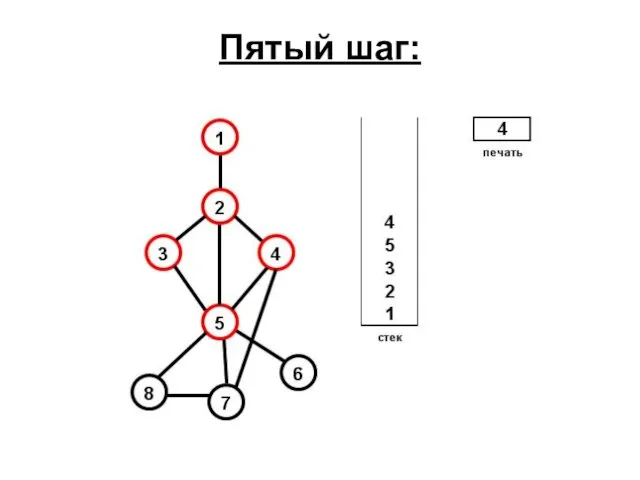
- 65. Пятый шаг:
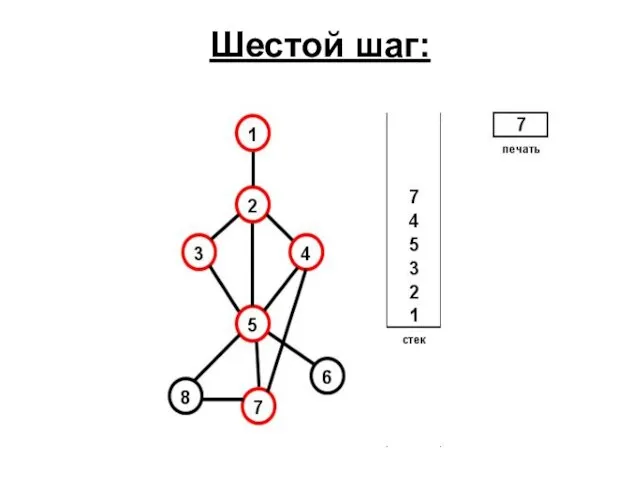
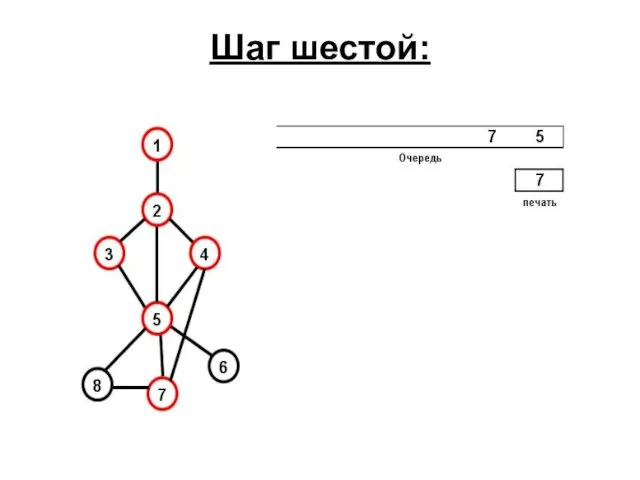
- 66. Шестой шаг:
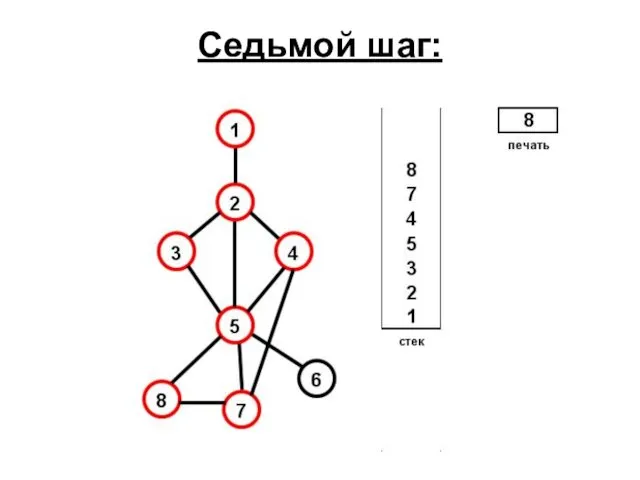
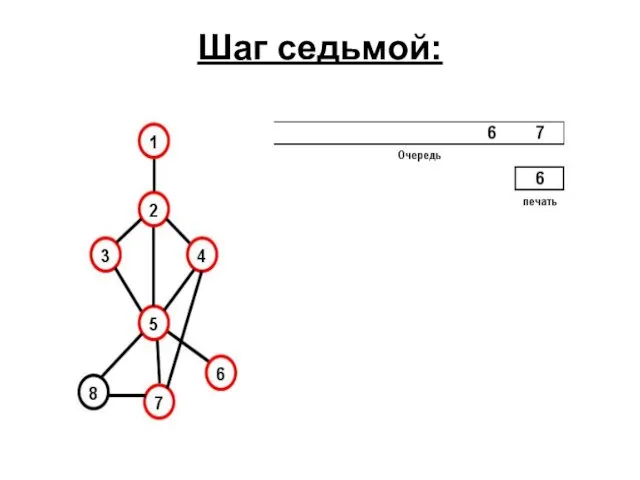
- 67. Седьмой шаг:
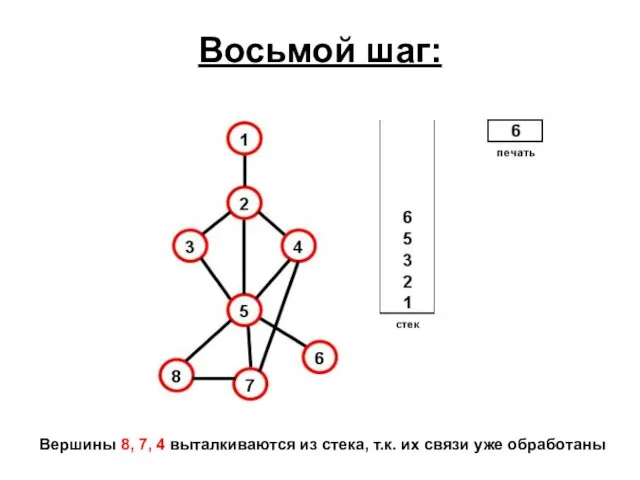
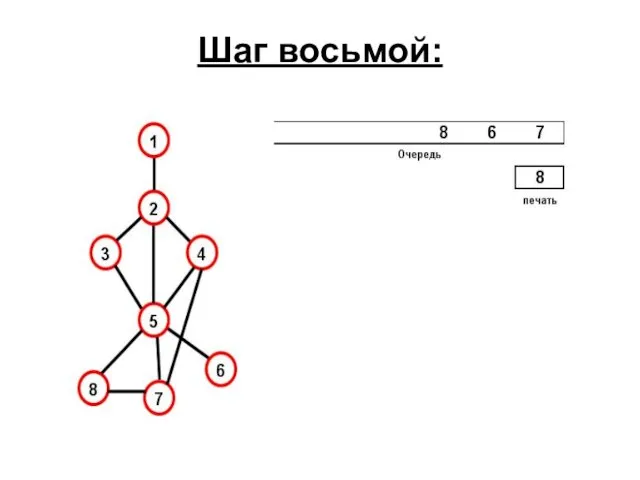
- 68. Восьмой шаг: Вершины 8, 7, 4 выталкиваются из стека, т.к. их связи уже обработаны
- 69. Далее все вершины будут вытолкнуты из стека. Получился следующий порядок обхода: 1,2,3,5,4,7,8,6
- 70. Теперь возьмем в качестве хранилища очередь. Будем использовать Алгоритм-2. Обход снова начнем с вершины 1.
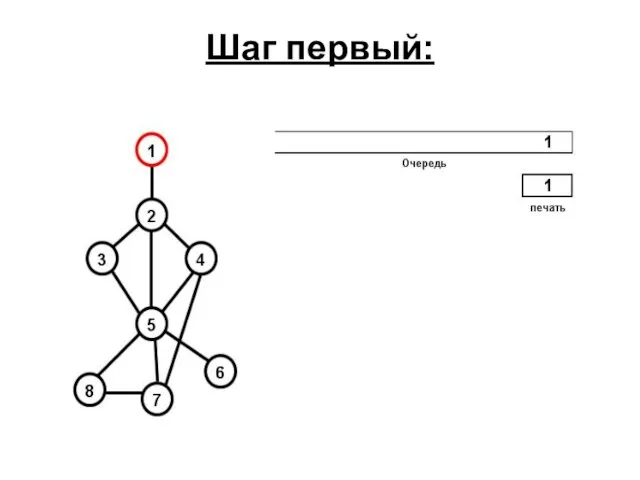
- 71. Шаг первый:
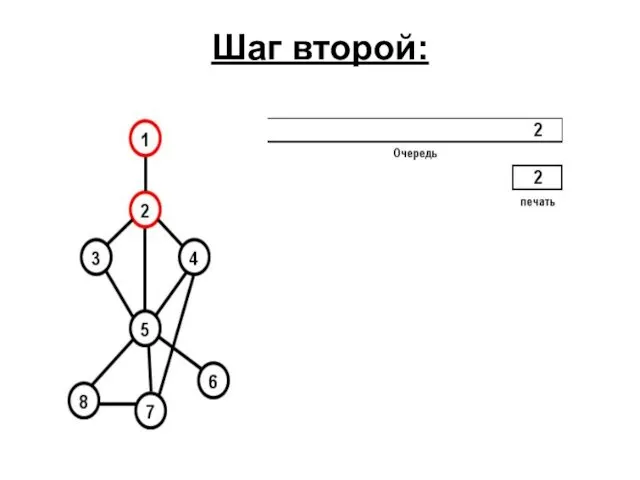
- 72. Шаг второй:
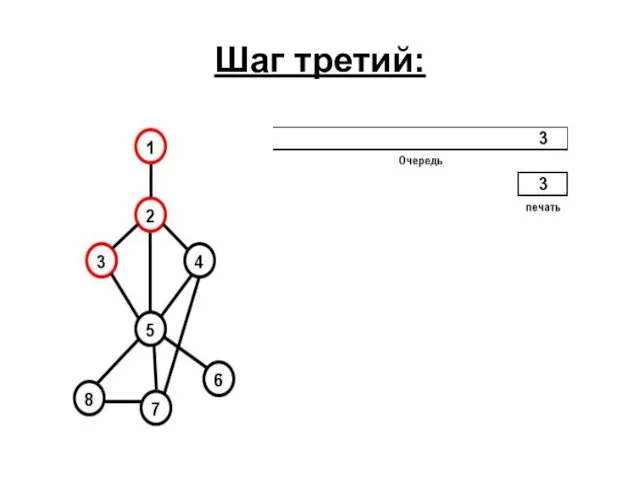
- 73. Шаг третий:
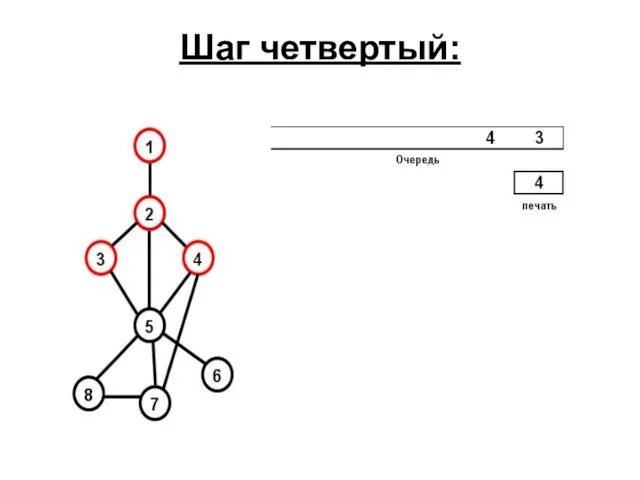
- 74. Шаг четвертый:
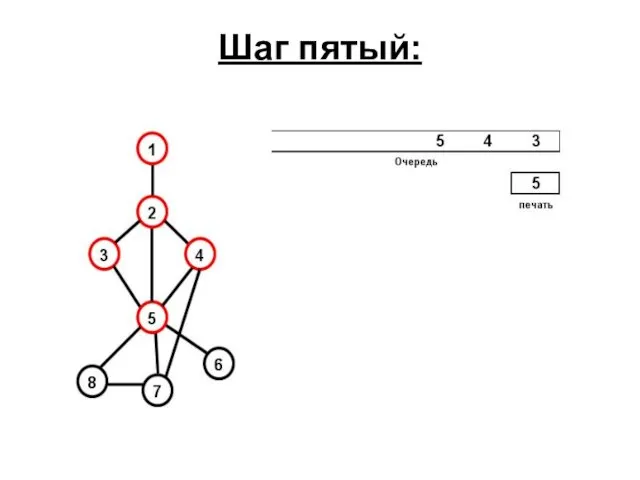
- 75. Шаг пятый:
- 76. Шаг шестой:
- 77. Шаг седьмой:
- 78. Шаг восьмой:
- 79. Получился следующий порядок обхода: 1,2,3,4,5,7,6,8
- 80. Замечание Оба алгоритма потребовали одинаковое число шагов. Почему? Потому, что при обходе каждая вершина печатается один
- 81. Поиск в глубину Перед выполнением поиска в глубину для графа с n вершинами заведем массив Chk
- 82. Алгоритм поиска в глубину с вершины p. Если Chk[p]=1 – выходим; Устанавливаем Chk[p]=1 Берем по очереди
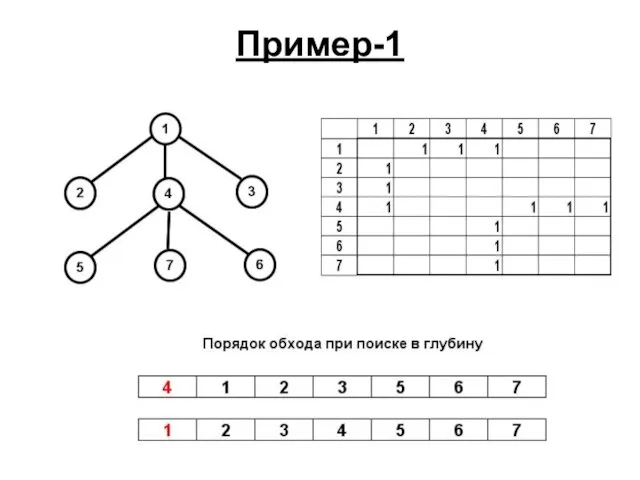
- 83. Пример-1
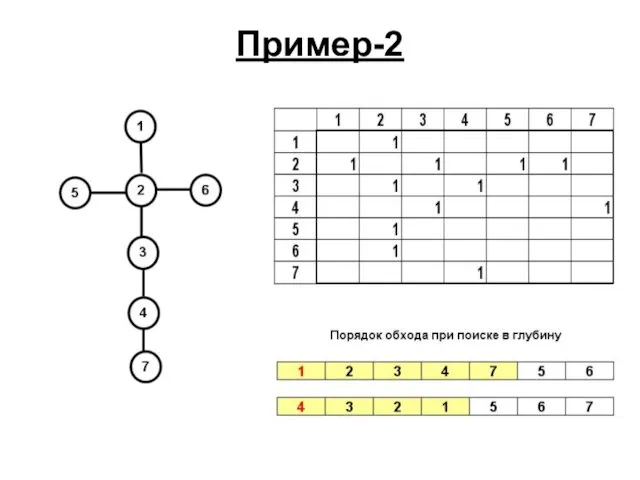
- 84. Пример-2
- 85. Если граф несвязный В этом случае после обхода останутся непросмотренные вершины. Можно повторить просмотр, начав с
- 86. Сложность алгоритма Вычислительная сложность алгоритма O(n+m), где n – число вершин, а m – число ребер
- 88. Скачать презентацию


































![Соглашение-3 Когда вершина j помещается в хранилище, она отмечается как просмотренная (т.е. устанавливается Chk[j]=1)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/470454/slide-53.jpg)










![Алгоритм поиска в глубину с вершины p. Если Chk[p]=1 – выходим;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/470454/slide-81.jpg)


 Линейные регрессионные модели с гетероскедастичными остатками
Линейные регрессионные модели с гетероскедастичными остатками Основы математического планирования эксперимента
Основы математического планирования эксперимента Аттестационная работа. Все профессии важны, с математикой дружны
Аттестационная работа. Все профессии важны, с математикой дружны Деление многозначного на трехзначное
Деление многозначного на трехзначное Основные тригонометрические формулы
Основные тригонометрические формулы Геометрическая прогрессия
Геометрическая прогрессия Все об окружности
Все об окружности Правильные многогранники (симметрия) 10 класс
Правильные многогранники (симметрия) 10 класс Презентация по математике "Простые и составные числа" - скачать бесплатно
Презентация по математике "Простые и составные числа" - скачать бесплатно Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Окружность. Центральные и вписанные углы. Решение задач на готовых чертежах
Окружность. Центральные и вписанные углы. Решение задач на готовых чертежах Математическая игра «Что? Где? Когда?»
Математическая игра «Что? Где? Когда?» Гетероскедастичность. Предпосылки МНК, связанные с ошибками
Гетероскедастичность. Предпосылки МНК, связанные с ошибками Методы параллельных вычислений
Методы параллельных вычислений Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Части графа. Операции над частями графа
Части графа. Операции над частями графа Частные производные функции нескольких переменных
Частные производные функции нескольких переменных МОУ «Средняя общеобразовательная школа №11» с. Юца, Предгорного района Ставропольского края Интегрированный урок (технологи
МОУ «Средняя общеобразовательная школа №11» с. Юца, Предгорного района Ставропольского края Интегрированный урок (технологи Формулы сокращенного умножения
Формулы сокращенного умножения Площадь прямоугольника. Разработка проекта учебного занятия по математике в 5 классе
Площадь прямоугольника. Разработка проекта учебного занятия по математике в 5 классе Принципы проектирования комбинационных логических схем
Принципы проектирования комбинационных логических схем В мире единиц длины
В мире единиц длины Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве
Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве Методы прогнозирования динамики экономических процессов
Методы прогнозирования динамики экономических процессов Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Симплекс. Симплексное планирование
Симплекс. Симплексное планирование Заинька. Математическая раскраска. Реши примеры и покажи ответы
Заинька. Математическая раскраска. Реши примеры и покажи ответы