Содержание
- 2. ЭЛЕМЕНТЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ 1.Первообразная и неопределенный интеграл 2.Своства интеграла, вытекающие из определения 3.Свойства интеграла 4. Таблица
- 3. Пусть X ⊂ R. Определение. Функция F(x), x ∈ X называется перво-образной для функции y =
- 4. Определение. Совокупность F(x) + С всех первообра-ных функции y = f(x) на множестве X называется неопределенным
- 5. СВОЙСТВА ИНТЕГРАЛОВ, ВЫТЕКАЮЩИЕ ИЗ ОПРЕДЕЛЕНИЯ Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал - подынтегральному
- 6. СВОЙСТВА ИНТЕГРАЛОВ
- 7. ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 9. СВОЙСТВА ДИФФЕРЕНЦИАЛОВ При интегрировании удобно пользоваться свойствами:
- 10. Во всех формулах этой таблицы в качестве и можно брать произвольную дифференцируемую функцию и = ϕ(х).
- 11. ПРИМЕР
- 12. МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 13. 1. Непосредственное интегрирование – интегрирование с помощью свойств, тождественных преобразований подынтегральной функции и таблицы основных интегралов.
- 14. 2. Интегрирование разложением. Интегрирование разложением есть приведение данного интеграла к сумме более простых интегралов. Пример. Вычислить
- 15. 2. Интегрирование по частям. Теорема. Если функции u(x) и v(x) дифференцируемы на некотором промежутке и на
- 16. ПРИМЕР
- 17. ПРИМЕРЫ
- 18. 3. Замена переменной. Метод заключается в переходе к новому аргументу интегрирования путём преобразования подынтегрального выражения по
- 19. Замечание. Используя простейшую замену переменной, легко получить следующие формулы:
- 20. ПРИМЕР Вычислим
- 21. Определение. Число b (действительное или комплексное) называется корнем полинома Pn(x), если Pn(b) = 0. Теорема 1.
- 22. Рациональной дробью называется дробь вида Pm(x) /Qn(x), где Pm(x) и Qn(x) – многочлены степени т и
- 23. Теорема. Пусть Pm(x) /Qn(x) − правильная рациональная дробь, знаменатель которой представлен в виде произведения линейных и
- 24. АЛГОРИТМ ИНТЕГРИРОВАНИЯ ДРОБНО-РАЦИОНАЛЬНОЙ ФУНКЦИИ 1. Если дробь неправильная, надо выделить целую часть рациональной дроби, разделив числитель
- 25. ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 1. 2. 3. Можно преобразовать каждое из произведений под знаком интеграла в алгебраическую
- 26. II. Интегралы вида , где n и m – целые. 1. Если n и m –
- 27. Пример. Вычислить
- 28. III. , где R – рациональная функция . 1. Универсальная подстановка: ⇒ , 2. Упрощенные подстановки.
- 29. Интеграл вида , где m, n, p – рациональные числа выражается через элементарные функции только в
- 30. Интегралы вида , где Pn (x) – многочлен степени выше второй, в общем случае не выражается
- 31. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- 32. Определение. Под определенным интегралом от данной непрерывной функции f(x) на данном отрезке [a,b] понимается соответствующее приращение
- 33. Пример. Найти интеграл от на отрезке [1; 3]. Решение.
- 34. 1. . 2. . 3. . 4. . 5. Если a 6. Если f (x) ≥
- 36. Скачать презентацию































![Пример. Найти интеграл от на отрезке [1; 3]. Решение.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/574386/slide-32.jpg)

 Числовые и буквенные выражения
Числовые и буквенные выражения Золотое сечение
Золотое сечение Сравнение рациональных чисел. 6 класс
Сравнение рациональных чисел. 6 класс Логарифмы и их применение
Логарифмы и их применение объём DVD диска
объём DVD диска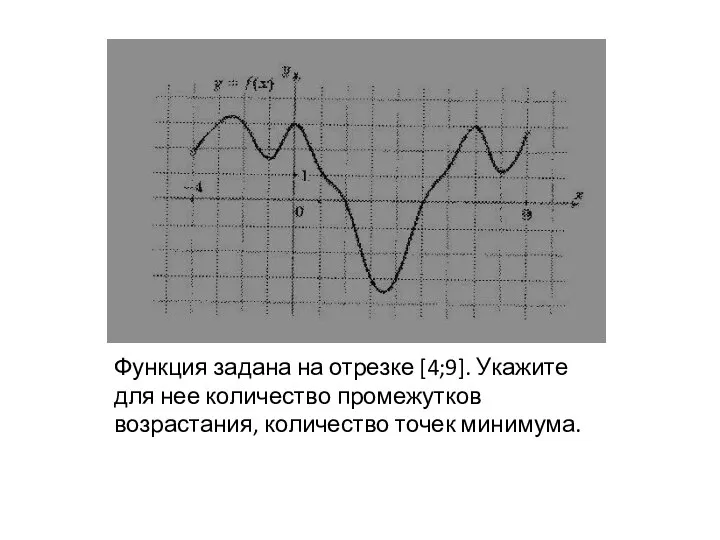 Использование производной для нахождения оптимального решения в прикладных задачах
Использование производной для нахождения оптимального решения в прикладных задачах Степени Понятие степени с натуральным показателем сформировалось ещё у древних народов.
Степени Понятие степени с натуральным показателем сформировалось ещё у древних народов. Сложение смешанных дробей
Сложение смешанных дробей Тренажёр Таблица сложения Автор:Самматова Эльмира Замиловна, учитель начальных классов
Тренажёр Таблица сложения Автор:Самматова Эльмира Замиловна, учитель начальных классов  Бесконечно убывающая геометрическая прогрессия
Бесконечно убывающая геометрическая прогрессия Геометрические фигуры
Геометрические фигуры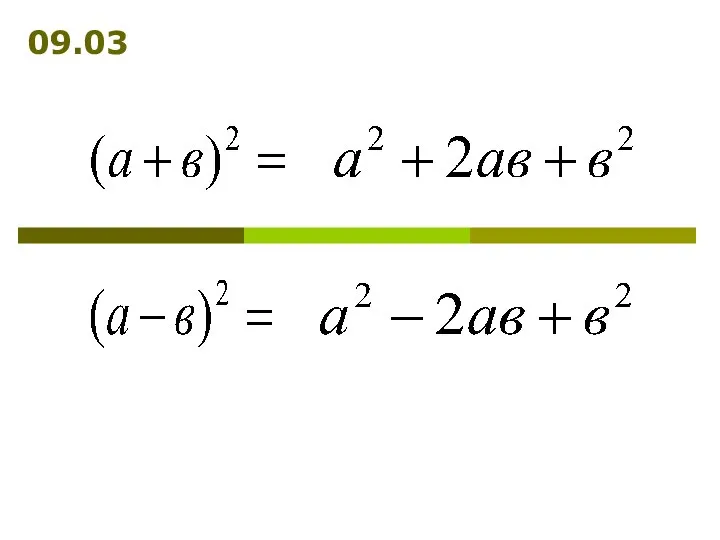 Преобразование многочленов с помощью формул сокращённого умножения
Преобразование многочленов с помощью формул сокращённого умножения Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс
Решение квадратных уравнений. Формулы корней квадратных уравнений. 8 класс Решение неравенств второй степени. Подготовка к ГИА. 9 класс
Решение неравенств второй степени. Подготовка к ГИА. 9 класс Математика вокруг нас
Математика вокруг нас Построение перпендикулярных прямых
Построение перпендикулярных прямых Тригонометрические формулы. (Лекция 4)
Тригонометрические формулы. (Лекция 4) Аттестационная работа. Образовательная программа внеурочной деятельности «В мире математики»
Аттестационная работа. Образовательная программа внеурочной деятельности «В мире математики»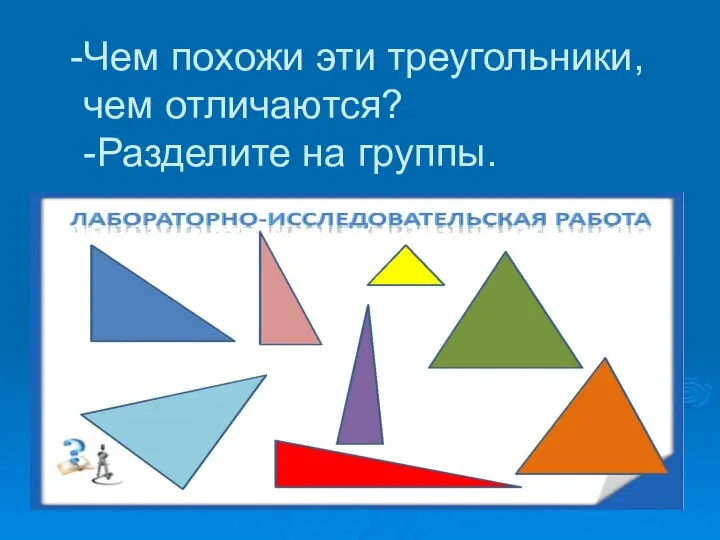 Классификация треугольников
Классификация треугольников Предсказание будущего
Предсказание будущего Проблема общезначимости формул алгебры предикатов
Проблема общезначимости формул алгебры предикатов Решение уравнений и задач на составление уравнения
Решение уравнений и задач на составление уравнения Функция нескольких переменных
Функция нескольких переменных Объем шарового сегмента, шарового слоя и шарового сектора
Объем шарового сегмента, шарового слоя и шарового сектора Презентация по математике "Шарады, метаграммы и логогрифы" - скачать бесплатно
Презентация по математике "Шарады, метаграммы и логогрифы" - скачать бесплатно Осевая и центральная симметрии
Осевая и центральная симметрии Арифметическая прогрессия
Арифметическая прогрессия Списки
Списки