Содержание
- 2. Формальная классификация моделей Формальная классификация моделей основывается на классификации используемых математических средств. Детерминированные ↔ стохастические Сосредоточенные
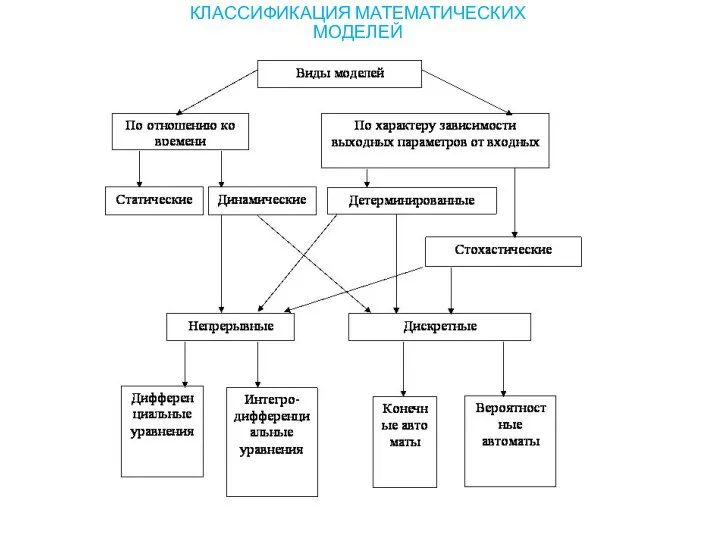
- 3. КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
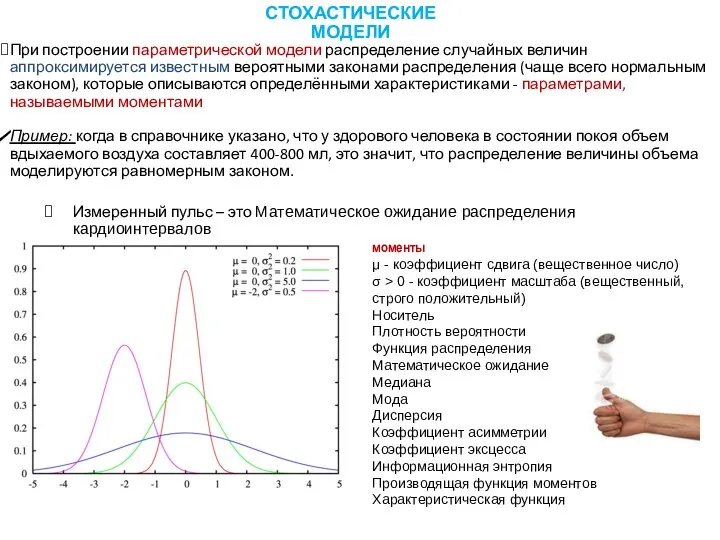
- 4. При построении параметрической модели распределение случайных величин аппроксимируется известным вероятными законами распределения (чаще всего нормальным законом),
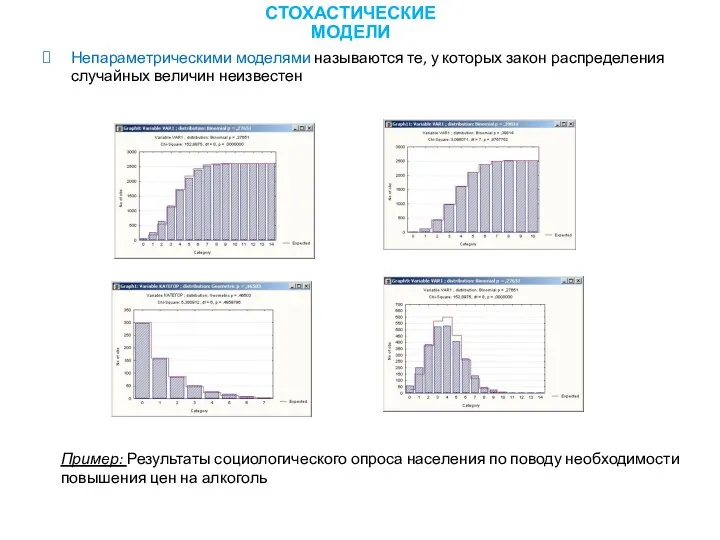
- 5. Непараметрическими моделями называются те, у которых закон распределения случайных величин неизвестен Пример: Результаты социологического опроса населения
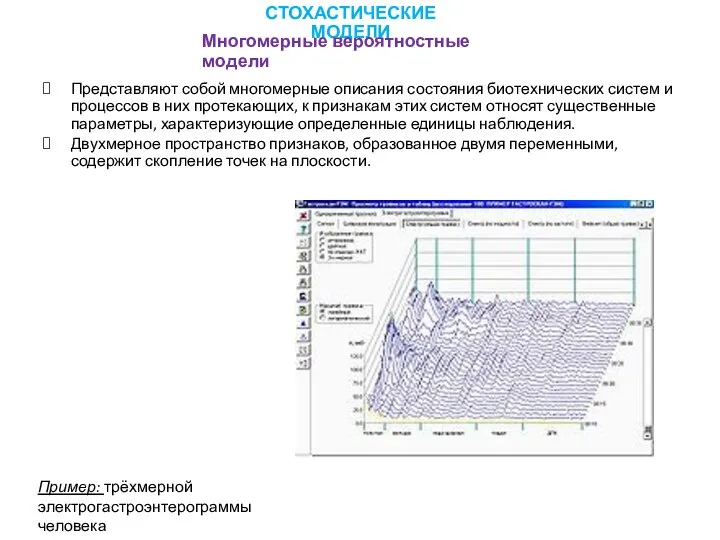
- 6. Представляют собой многомерные описания состояния биотехнических систем и процессов в них протекающих, к признакам этих систем
- 7. (от лат. factor — действующий, производящий и греч. analysis — разложение, расчленение) — совокупность методов, которые
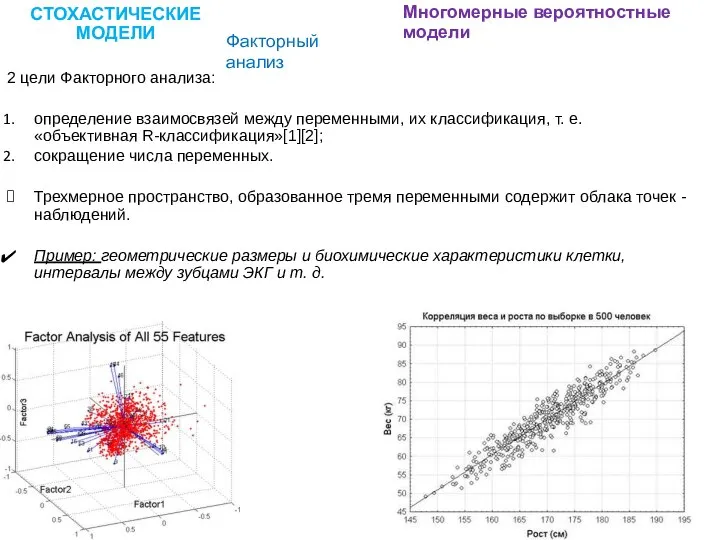
- 8. СТОХАСТИЧЕСКИЕ МОДЕЛИ Многомерные вероятностные модели 2 цели Факторного анализа: определение взаимосвязей между переменными, их классификация, т.
- 9. Ковариация СТОХАСТИЧЕСКИЕ МОДЕЛИ Многомерные вероятностные модели Факторный анализ где М — математическое ожидание. Линейный коэффициент корреляции
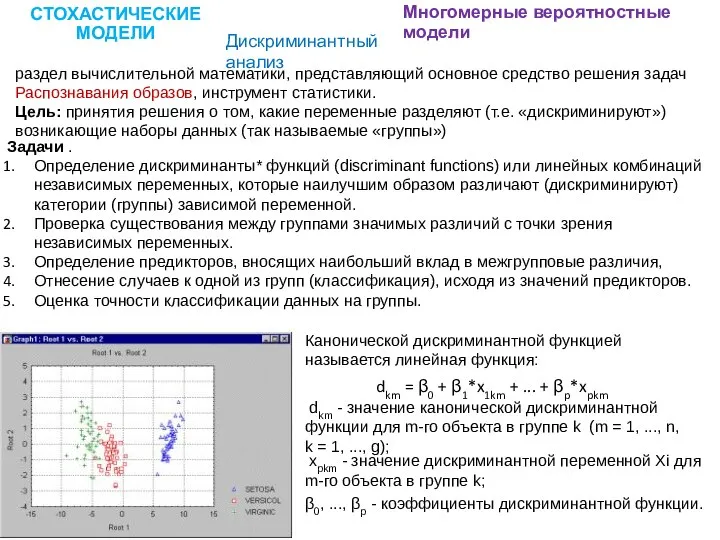
- 10. СТОХАСТИЧЕСКИЕ МОДЕЛИ Многомерные вероятностные модели Дискриминантный анализ раздел вычислительной математики, представляющий основное средство решения задач Распознавания
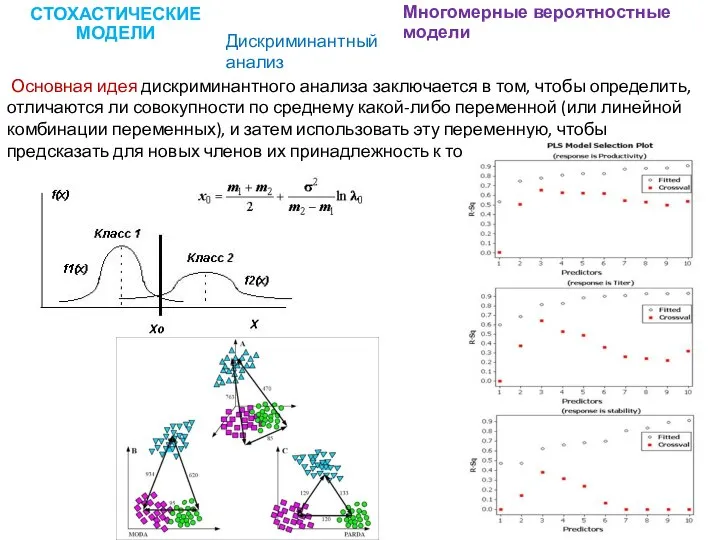
- 11. СТОХАСТИЧЕСКИЕ МОДЕЛИ Многомерные вероятностные модели Дискриминантный анализ Основная идея дискриминантного анализа заключается в том, чтобы определить,
- 12. СТОХАСТИЧЕСКИЕ МОДЕЛИ Многомерные вероятностные модели Кластерный анализ - это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое
- 13. Параметрическое представление — используемая в математическом анализе разновидность представления переменных, когда их зависимость выражается через дополнительную
- 14. а) С непрерывным пространством и временем представляют собой функциональные или аналитические зависимости. Эти модели чаще всего
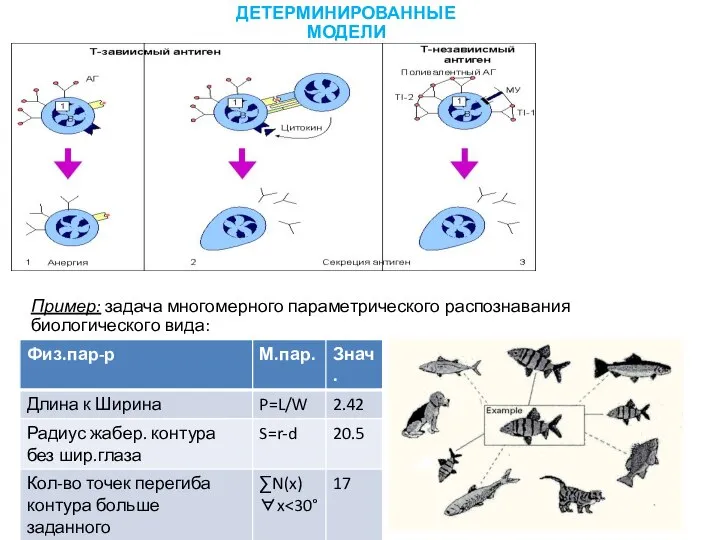
- 15. Пример: задача многомерного параметрического распознавания биологического вида: ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
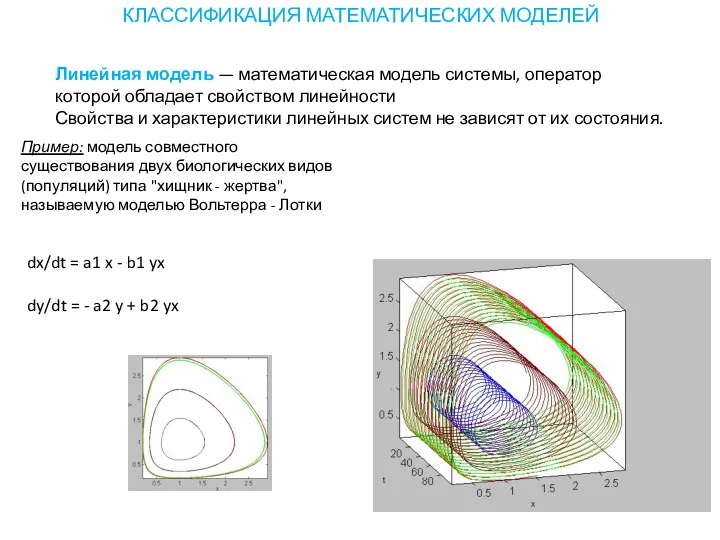
- 16. Линейная модель — математическая модель системы, оператор которой обладает свойством линейности Свойства и характеристики линейных систем
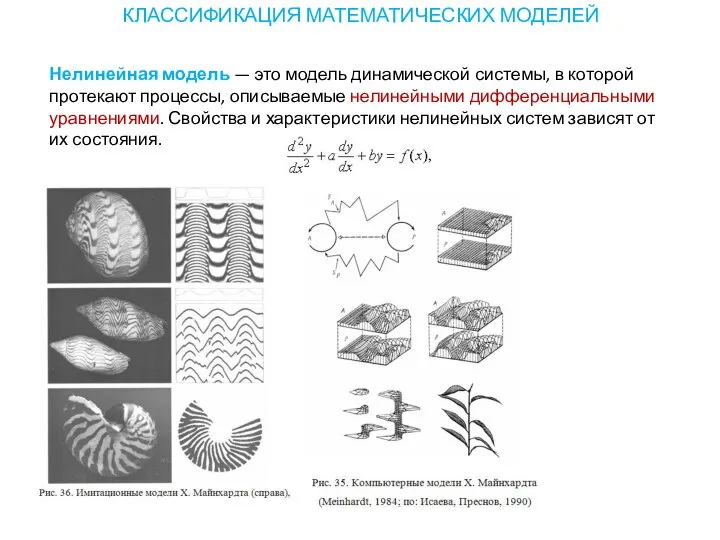
- 17. КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ Нелинейная модель — это модель динамической системы, в которой протекают процессы, описываемые нелинейными
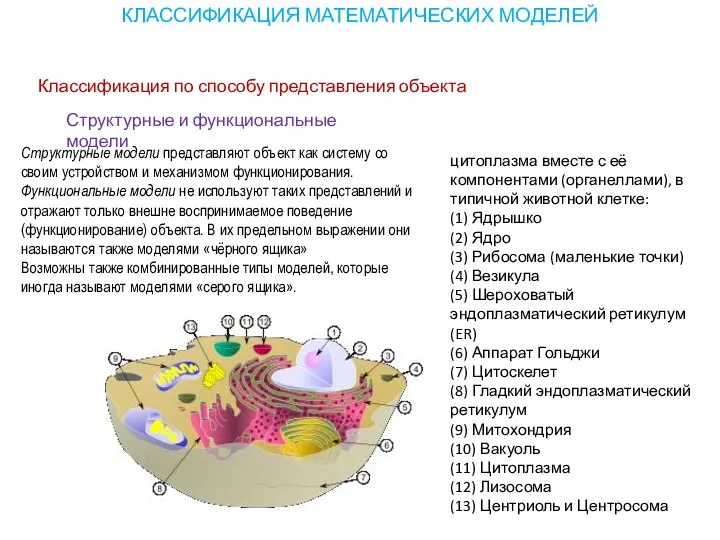
- 18. Классификация по способу представления объекта КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ цитоплазма вместе с её компонентами (органеллами), в типичной
- 20. Скачать презентацию






 Урок математики во 2 классе. Школа России. Подготовила и провела учитель начальных классов МБОУ «СОШ №2» г. Емвы Республики Коми
Урок математики во 2 классе. Школа России. Подготовила и провела учитель начальных классов МБОУ «СОШ №2» г. Емвы Республики Коми Основы метрологии
Основы метрологии Площади параллелограмма, треугольника, трапеции. Подготовка к ГИА
Площади параллелограмма, треугольника, трапеции. Подготовка к ГИА Разгадайте загадки
Разгадайте загадки Разбор заданий математической регаты
Разбор заданий математической регаты Площадь треугольника
Площадь треугольника Градусная мера дуги
Градусная мера дуги Osnovy_teorii_veroyatnostey
Osnovy_teorii_veroyatnostey Признаки равенства прямоугольных теугольников
Признаки равенства прямоугольных теугольников Системы линейных уравнений. Основные понятия
Системы линейных уравнений. Основные понятия Интервальные оценки. Проверка статистических гипотез. (повторение)
Интервальные оценки. Проверка статистических гипотез. (повторение) Презентация по математике "Парабола. Родственники параболы ближние и дальние." - скачать
Презентация по математике "Парабола. Родственники параболы ближние и дальние." - скачать  Ідентифікація сушки сипучих речовин
Ідентифікація сушки сипучих речовин Решение уравнений и неравенств, содержащих параметр, с использованием параллельного переноса вдоль оси Oy
Решение уравнений и неравенств, содержащих параметр, с использованием параллельного переноса вдоль оси Oy Формирование вычислительной культуры учащихся по математике в 5,6 классах
Формирование вычислительной культуры учащихся по математике в 5,6 классах Её величество Степень
Её величество Степень Правильные многогранники
Правильные многогранники Треугольник
Треугольник Сумма векторов. Правила сложения векторов
Сумма векторов. Правила сложения векторов Лекция 6. Методы численного интегрирования
Лекция 6. Методы численного интегрирования Векторная алгебра
Векторная алгебра  Обыкновенные дроби
Обыкновенные дроби Тренажёр. Таблица умножения
Тренажёр. Таблица умножения Несобственные интегралы
Несобственные интегралы Презентация на тему Язык уравнений
Презентация на тему Язык уравнений  ВЕКТОРЫ НА ПЛОСКОСТИ
ВЕКТОРЫ НА ПЛОСКОСТИ  Разность
Разность Реализация элементов технологии развития критического мышления на уроках математики Куракина Н.Ю. учитель матем
Реализация элементов технологии развития критического мышления на уроках математики Куракина Н.Ю. учитель матем