Содержание
- 2. First, a Word About Hammers requirements for this to be a good idea a way of
- 3. Hammers (cont.) by definition, not the optimal way to solve problems, BUT computers are very fast
- 4. What are “advanced game math problems”? problems that are ammenable to mathematical modeling state the problem
- 5. Prerequisites linear algebra vector, matrix symbol manipulation at least calculus concepts what derivatives mean comfortable with
- 6. Overview of Lecture random assortment of example problems breifly mentioned 5 specific example problems in some
- 7. A Look Forward linear equations Ax = b linear inequalities Ax >= b linear programming min
- 8. Applications to Games graphics, physics, ai, even ui computational geometry visibility contact curve fitting constraints integration
- 9. Applications to Games (cont.) don’t forget... The Elastohydrodynamic Lubrication Problem Solving Optimal Ownership Structures “The two
- 10. Specific Examples #1a: Ease Cubic Fitting warm up with an ease curve cubic x(t)=at3+bt2+ct+d x’(t)=3at2+2bt+c 4
- 11. Specific Examples #1a: Ease Cubic Fitting (cont.) x(t)=at3+bt2+ct+d, x’(t)=3at2+2bt+c x(0) = a03+b02+c0+d = d = 0
- 12. Specific Examples #1a: Ease Cubic Fitting (cont.) d = 0, a+b+c+d = 1, c = 0,
- 13. Specific Examples #1a: Ease Cubic Fitting (cont.) or, x(0) = d = 0 x(1) = a
- 14. Specific Examples #1b: Cubic Spline Fitting same technique to fit higher order polynomials, but they “wiggle”
- 15. Specific Examples #1b: Cubic Spline Fitting (cont.) a0 b0 c0 d0 a1 b1 c1 d1 .
- 16. Specific Examples #2: Minimum Cost Network Flow what is the cheapest flow route(s) from sources to
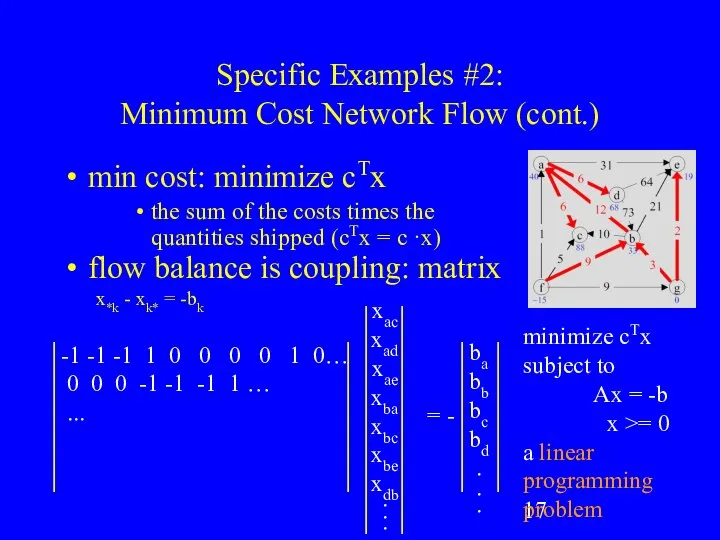
- 17. Specific Examples #2: Minimum Cost Network Flow (cont.) min cost: minimize cTx the sum of the
- 18. Specific Examples #3: Points in Polys point in convex poly defined by planes n1 · x
- 19. Specific Examples #3: Points in Polys (cont.) closest point in two polys min (x2-x1)2 s.t. A1x1
- 20. Specific Examples #3: Points in Polys (cont.) how do we stack x1,x2 into single x given
- 21. Specific Examples #3: Points in Polys (cont.) more points, more polys! min (x2-x1)2 + (x3-x2)2 +
- 22. Specific Examples #4: Contact model like IK constraints a = Af + b a >= 0,
- 23. Specific Examples #5: Joint Limits in CCD IK how to do child-child constraints in CCD? parent-child
- 24. What Unifies These Examples? linear equations Ax = b linear inequalities Ax >= b linear programming
- 25. QP is a Superset of Most quadratic programming min ½xTQx + cTx s.t. Ax >= b
- 26. Karush-Kuhn-Tucker Optimality Conditions get us to MLCP for QP form “Lagrangian” L(x,u,v) = ½ xTQx +
- 27. Karush-Kuhn-Tucker Optimality Conditions (cont.) L(x,u,v) = ½ xTQx + cTx - uT(Ax - b) - vT(Dx
- 28. This is an MLCP x v u Q -DT -AT D 0 0 A 0 0
- 29. Modeling Summary a lot of interesting problems can be formulated as MLCPs model the problem mathematically
- 30. Solving MLCPs (where I hope I made you hungry enough for homework) Lemke’s Algorithm is only
- 31. Playing Around With MLCPs PATH, a MCP solver (superset of MLCP!) really stoked professional solver free
- 32. References for Lemke, etc. free pdf book by Katta Murty on LCPs, etc. free pdf book
- 34. Specific Examples #5: Constraints for IK compute “forces” to keep bones together a1 = A11 f1
- 36. Скачать презентацию
































 Основные структурные изменения и особенности проведения государственной аттестации учащихся в 2015. Занятие №1
Основные структурные изменения и особенности проведения государственной аттестации учащихся в 2015. Занятие №1 Прямоугольник. Урок математики. 2 класс
Прямоугольник. Урок математики. 2 класс Презентация по математике "ПРОПОРЦИЯ" - скачать бесплатно
Презентация по математике "ПРОПОРЦИЯ" - скачать бесплатно Аксиоматические теории первого порядка
Аксиоматические теории первого порядка GEOMETRIYa_povtorenie
GEOMETRIYa_povtorenie Применение свойств арифметических действий сложения и вычитания для рационализации вычисления
Применение свойств арифметических действий сложения и вычитания для рационализации вычисления Решение логических задач. Лекция №13
Решение логических задач. Лекция №13 Дробь: числитель и знаменатель, делимое и делитель
Дробь: числитель и знаменатель, делимое и делитель Метод экспертного оценивания. Обобщение мнений экспертов
Метод экспертного оценивания. Обобщение мнений экспертов Конус та його елементи
Конус та його елементи Множества и отношения
Множества и отношения Квадратная решетка. Координатная плоскость
Квадратная решетка. Координатная плоскость Математика – великая и разная (лекция 2)
Математика – великая и разная (лекция 2) Золотое сечение в искусстве Выполнен учащейся 4 класса МОУ ДОД «Котовская детская школа искусств» Тамбовской области Поповой
Золотое сечение в искусстве Выполнен учащейся 4 класса МОУ ДОД «Котовская детская школа искусств» Тамбовской области Поповой  Решение логарифмических неравенств
Решение логарифмических неравенств Урок-практикум «Логарифмические уравнения и неравенства» Учитель математики МОУ «СОШ №1 р.п. Новые Бурасы Новобурасского
Урок-практикум «Логарифмические уравнения и неравенства» Учитель математики МОУ «СОШ №1 р.п. Новые Бурасы Новобурасского  Фрактальная графика. Понятие фрактала
Фрактальная графика. Понятие фрактала Преобразование графиков функций. Памятка для учащихся
Преобразование графиков функций. Памятка для учащихся Метапредметные результаты. Компетентностноориентированные задания. 9 класс
Метапредметные результаты. Компетентностноориентированные задания. 9 класс Дивовижне число Пі
Дивовижне число Пі Формулы двойного аргумента
Формулы двойного аргумента Многомерный регрессионный анализ. Основные задачи регрессионного анализа
Многомерный регрессионный анализ. Основные задачи регрессионного анализа Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена
Алгебра. Лекция 4. Количество и сумма натуральных делителей числа. Критерий простоты. Решето Эратосфена Решение задач на проценты (%)
Решение задач на проценты (%) Решение планиметрических задач на стереометрических чертежах
Решение планиметрических задач на стереометрических чертежах Линейная функция. Открытый урок по алгебре в 7 классе
Линейная функция. Открытый урок по алгебре в 7 классе Множества
Множества Основы теории ошибок измерений. Виды измерений и погрешностей
Основы теории ошибок измерений. Виды измерений и погрешностей