Содержание
- 2. Разделы математики 1.Линейная и векторная алгебра 2. Аналитическая геометрия 3.Функции. Дифференциальное исчисление. --------------------------------------------- 4. Интегральное исчисление.
- 3. ППИ,1 курс 1 семестр: 1 лекция (2 ч); практ.занятий (6 ч и зачет). Контрольная работа, зачет
- 4. Балльно-рейтинговая система 1 курс Он-лайн 1 лекции 5 баллов (max 1*5=5); 3 лаб. занятия по 5
- 5. МАТЕМАТИКА Раздел 1. ЛИНЕЙНАЯ и ВЕКТОРНАЯ АЛГЕБРА Лекция № 1. Матрицы. Действия над матрицами. Определители и
- 6. ЛИТЕРАТУРА (ППИ) Худякова М.М., Фалькова О.Н, Основы высшей математики. Данко П.Е., Попов А.Г и др. Высшая
- 7. Учебные вопросы. 1. Линейные операции над матрицами. Произведение и транспонирование матриц. 2. Вычисление ранга матрицы путем
- 8. Введение в дисциплину Линейная алгебра – раздел алгебры, изучающий линейные и векторные пространства. Исторически первым разделом
- 9. 1 Учебный вопрос. Линейные операции над матрицами. (Правило сложения , вычитания матриц. Правило умножения матрицы на
- 10. Определение . Числовой матрицей размерности m×n называется прямоугольная таблица чисел состоящая из m строк и n
- 11. Принятые обозначения матрицы: Прописные буквы латинского алфавита A, B, C, … Am×n ,если хотят указать размерность
- 12. Определение . Матрицы A и B называются равными матрицами, если они одинаковой размерности и все их
- 13. Определение. Матрица называется квадратной матрицей, если число её строк равно числу её столбцов, т.е. m=n. Определение.
- 14. Определение. Квадратная матрица называется диагональной матрицей, если на главной диагонали расположены числа, отличные от нуля, вне
- 15. Сложение и вычитание матриц Сложение и вычитание матриц определено только для матриц одинаковой размерности. Определение. Суммой
- 16. Пример . Даны матрицы Найти C=А +B. Решение
- 17. Свойства сложения A+B=B+A (A+B)+C=A+(B+C) A+0=A, где O – нулевая матрица такой же размерности, как и матрица
- 18. Умножение матрицы на число Это матрица, полученная умножением соответствующих элементов на данное число
- 19. Транспонирование матриц Определение. Матрицу AT называют транспонированной матрицей к данной матрице А, если элементы каждой строки
- 20. Умножение матриц Определение. Произведением матрицы Am×n на матрицу Bn×k называется матрица Cm×k= A·B , имеющая m
- 21. Пример умножения матриц
- 22. Учебный вопрос. Определители второго и третьего порядков, их вычисление . (Правило вычисления определителя II порядка. Правило
- 24. Если порядок матрицы равен трем (n =3), то определителем третьего порядка назовем число, вычисленное по формуле:
- 25. 1 способ) Данную формулу можно запомнить приписав к определителю первые два столбца. Со знаком плюс берутся
- 26. Или, 2 способ) используем правило треугольников: В этой схеме плюс означает, что произведения указанных элементов берутся
- 27. Пример. Вычислить определитель приписыванием первых двух столбцов Решение.
- 29. Пример . Для определителя |A| укажем некоторые миноры и алгебраические дополнения:
- 30. Учебный вопрос Свойства определителя.
- 31. Свойства определителей. (дз) 1. При транспонировании матрицы ее определитель не изменяется: 2. При перестановке двух строк
- 32. Алгоритм вычисления определителя методом приведения его к треугольному виду.
- 33. 6. Определитель не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца),
- 34. 8.Определитель, все элементы i-ой строки (столбца) которого представляют сумму двух слагаемых, равна сумме двух определителей, все
- 35. Учебный вопрос . Разложение определителя по элементам строки или столбца матрицы (теорема Лапласа).
- 36. Определение. Определителем матрицы n-го порядка называется число, которое сопоставляется квадратной матрице n-го порядка, получаемое по определенному
- 37. Теорема Лапласа. Определитель матрицы n-го порядка равен сумме произведений элементов какой-либо строки (или столбца) на их
- 41. Алгоритм вычисления определителя методом эффективного понижения порядка. 1) Выбрать «ряд» определителя (строку или столбец), содержащий нуль
- 42. Раздел 1. ЛИНЕЙНАЯ и ВЕКТОРНАЯ АЛГЕБРА Обратная матрица. Ранг матрицы. Основные сведения о СЛУ. Методы решения
- 43. ЛИТЕРАТУРА (ППИ) Данко П.Е., Попов А.Г и др. Высшая математика в упражнениях и задачах, части I,II.
- 44. Учебный вопрос . Алгоритм отыскания обратной матрицы
- 45. Определение. Квадратная матрица называется вырожденной матрицей, если её определитель равен нулю. Квадратная матрица А называется невырожденной
- 46. Теорема об обратной матрице Если квадратная матрица А невырожденная, то существует обратная матрица и находим ее
- 47. Формула для обратной матрицы 3-его порядка:
- 48. Алгоритм составления обратной матрицы: 1) 2)
- 49. Пример. Найти матрицу, обратную данной А =
- 50. Воспользуемся формулой
- 54. Скачать презентацию


















































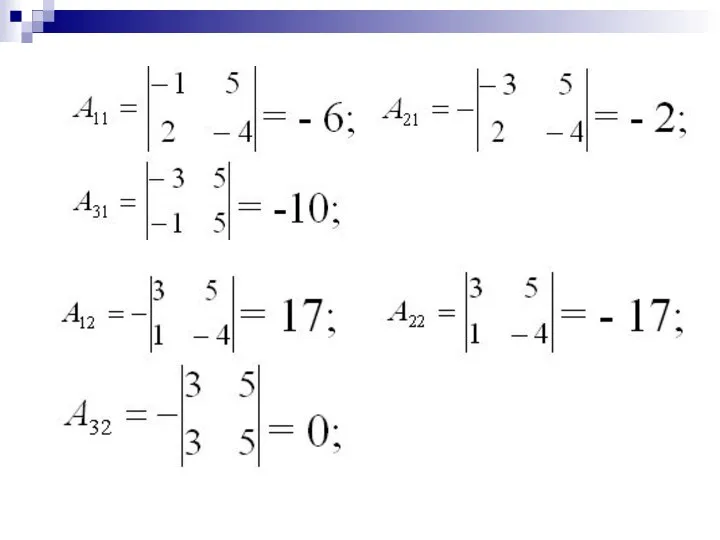
 Квадратичная функция у=х2 и ее свойства
Квадратичная функция у=х2 и ее свойства Сложение и вычитание дробей
Сложение и вычитание дробей Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак
Числові характеристики випадкових величин, показники варіації; первинна статистична обробка кількісних ознак Тренажёр. Табличное умножение и деление. Сложение и вычитание. Поиграем, посчитаем. 2-3 классы
Тренажёр. Табличное умножение и деление. Сложение и вычитание. Поиграем, посчитаем. 2-3 классы Задачи на готовых чертежах (Теорема Пифагора)
Задачи на готовых чертежах (Теорема Пифагора) Решение уравнений. (6 класс)
Решение уравнений. (6 класс) Признаки делимости
Признаки делимости Тренажер Таблица умножения трёх
Тренажер Таблица умножения трёх Тригонометрические формулы
Тригонометрические формулы Теорема Пифагора
Теорема Пифагора Умение читать свойства функции по графику
Умение читать свойства функции по графику Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Предел функции
Предел функции Площадь параллелограмма
Площадь параллелограмма История создания мер длины
История создания мер длины Решение простейших тригонометрических уравнений с помощью единичной окружности
Решение простейших тригонометрических уравнений с помощью единичной окружности Обратные тригонометрические функции
Обратные тригонометрические функции Математика – симфония чисел
Математика – симфония чисел Основы математической обработки информации
Основы математической обработки информации Презентация по математике "Математика в 1-м классе" - скачать бесплатно
Презентация по математике "Математика в 1-м классе" - скачать бесплатно Алгебраический марафон №1 по пройденным темам
Алгебраический марафон №1 по пройденным темам Квадрат суммы. Квадрат разности
Квадрат суммы. Квадрат разности Деление одночленов
Деление одночленов Презентация по математике "Расположение точек относительно осей координат" - скачать бесплатно
Презентация по математике "Расположение точек относительно осей координат" - скачать бесплатно Квадартные уравнения. Основные понятия
Квадартные уравнения. Основные понятия Симметрия в пространстве
Симметрия в пространстве Лекция 21
Лекция 21 Таблицы, часть 1, 5-9 классы
Таблицы, часть 1, 5-9 классы