Содержание
- 2. Балльно-рейтинговая система 1 курс Он-лайн 1 лекции 5 баллов (max 1*5=5); 3 лаб. занятия по 5
- 3. 3.Учебный вопрос. Метод Гаусса систем линейных алгебраических уравнений.
- 4. Карл Фридрих Гаусс (30.04.1777-23.02.1855) Немецкий математик, механик, физик, астроном и геодезист. Считается одним из величайших математиков
- 5. Рассмотрим систему m линейных алгебраических уравнений с n неизвестными. Расширенной матрицей системы называется основная матрица с
- 6. Напомним, элементарными преобра-зованиями строк матрицы называются: 1) перемена местами двух строк матрицы; 2) умножение строки на
- 7. Напомним, рангом матрицы размерности m×n называется количество ненулевых строк в эквивалентной ей ступенчатой матрице. Ступенчатая матрица
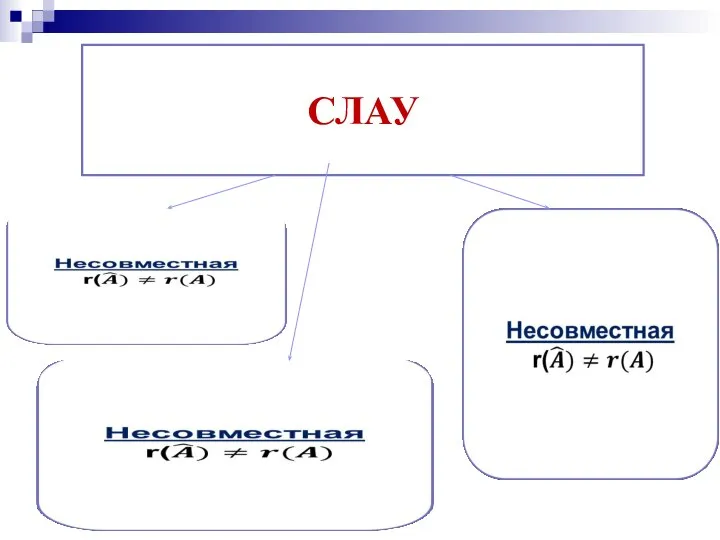
- 8. Определение. Две системы линейных алгебраических уравнений называются эквивалентными или равносильными, если они имеют одно и то
- 9. Метод Гаусса. В отличие от матричного метода и метода Крамера метод Гаусса может быть применен к
- 10. Алгоритм решения систем линейных уравнений методом Гаусса .
- 11. 1)Расширенную матрицу системы с помощью элементарных преобразований приводим к ступенчатому виду. 2)Отбрасываем нулевые строки. 3) Применяем
- 12. СЛАУ
- 13. Если система имеет единственное решение, то, двигаясь по системе снизу вверх, последовательно находим значения неизвестных. Если
- 14. 4) Неизвестная, соответствующая столбцу, в котором стоит первый ненулевой элемент данной строки, является базисной. Остальные неизвестные
- 15. Пример. Решить систему методом Гаусса. Решение. –2 –1 –2 3 + +
- 16. + 1/5
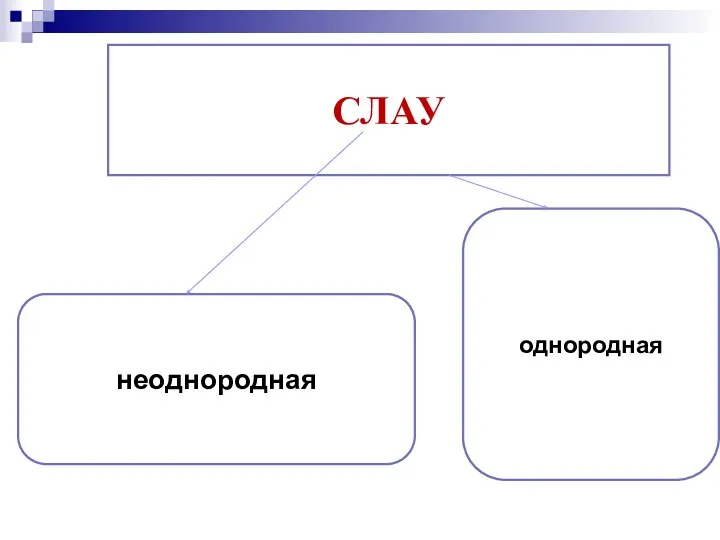
- 17. однородная неоднородная СЛАУ
- 18. Система линейных алгебраических уравнений называется однородной СЛАУ, если свободный член в каждом уравнении равен нулю. Пример.
- 19. Очевидно, что x1=x2=…=xn=0 – нулевое или тривиальное решение однородной системы. Кроме тривиального, система может иметь и
- 21. Скачать презентацию
















 Параллельность прямых, прямой и плоскости
Параллельность прямых, прямой и плоскости Пирамида. Теорема о площади боковой поверхности правильной пирамиды
Пирамида. Теорема о площади боковой поверхности правильной пирамиды Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций
Метод интегрирования по частям в неопределенном интеграле. Интегрирование тригонометрических функций Одночлен и его стандартный вид
Одночлен и его стандартный вид Основные законы теории вероятности
Основные законы теории вероятности Многочлен и его стандартный вид
Многочлен и его стандартный вид Поверхности второго порядка. Поверхности, образованные вращением некоторых кривых второго порядка. Цилиндрические поверхности
Поверхности второго порядка. Поверхности, образованные вращением некоторых кривых второго порядка. Цилиндрические поверхности Прямая и обратная пропорциональность. Решение задач
Прямая и обратная пропорциональность. Решение задач Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Классификация погрешностей
Классификация погрешностей ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. Подготовка к ЕГЭ.
ЗАДАНИЯ С РАЗВЕРНУТЫМ ОТВЕТОМ ПОВЫШЕННОГО УРОВНЯ СЛОЖНОСТИ С5. Подготовка к ЕГЭ.  Задачи по математике
Задачи по математике Здоровьесберегающие технологии на уроках математики
Здоровьесберегающие технологии на уроках математики Задачи со спичками
Задачи со спичками Занимательные задачи по математике (5 класс)
Занимательные задачи по математике (5 класс) Материалы к урокам и факультативным занятиям для 11 класса
Материалы к урокам и факультативным занятиям для 11 класса Односторонние пределы
Односторонние пределы Функции тангенса и котангенса
Функции тангенса и котангенса Понятие булева вектора (двоичного вектора)
Понятие булева вектора (двоичного вектора) Задачи по готовым чертежам. Внешний угол треугольника
Задачи по готовым чертежам. Внешний угол треугольника Умножение и деление.Задачи
Умножение и деление.Задачи Площадь прямоугольника
Площадь прямоугольника Решение логических задач с помощью кругов Эйлера Занятие 1
Решение логических задач с помощью кругов Эйлера Занятие 1 Интегрирование функции одной переменной
Интегрирование функции одной переменной Задачи на движение. Математические модели
Задачи на движение. Математические модели Умножение. Координаты точки
Умножение. Координаты точки Задачи на деление и умножение
Задачи на деление и умножение