Содержание
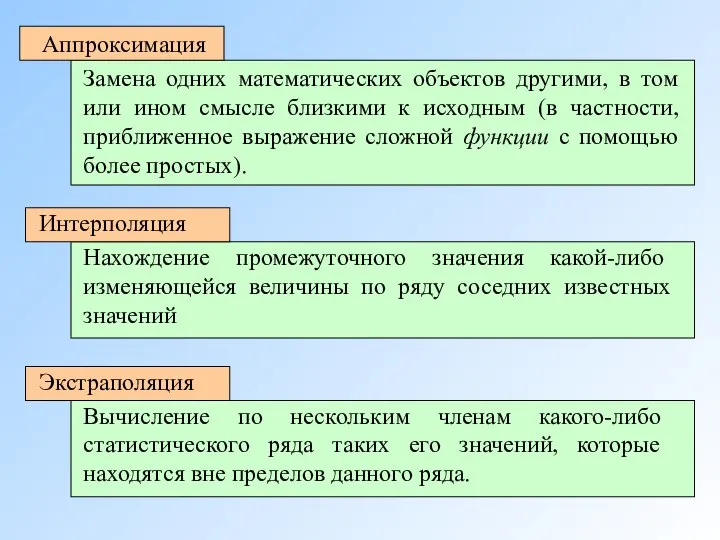
- 2. Аппроксимация Замена одних математических объектов другими, в том или ином смысле близкими к исходным (в частности,
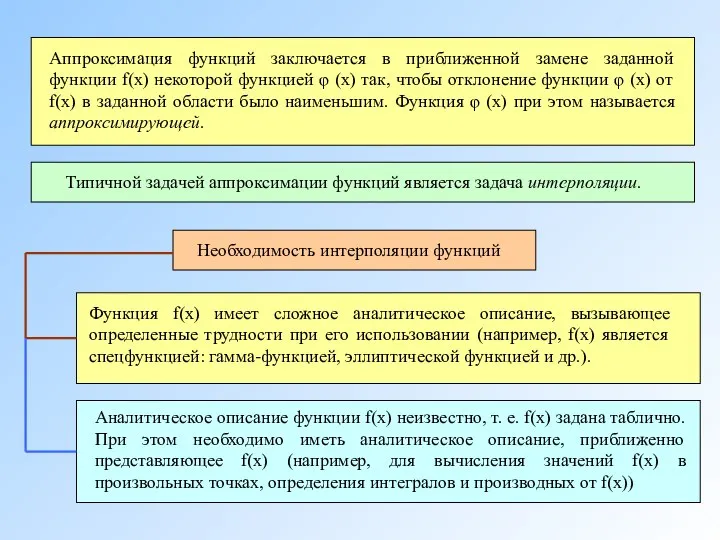
- 3. Аппроксимация функций заключается в приближенной замене заданной функции f(x) некоторой функцией φ (x) так, чтобы отклонение
- 4. На отрезке [a, b] заданы n + 1 точки xi = х0, х1, . . .,
- 5. В такой общей постановке задача может иметь бесконечное множество решений или совсем не иметь решений.
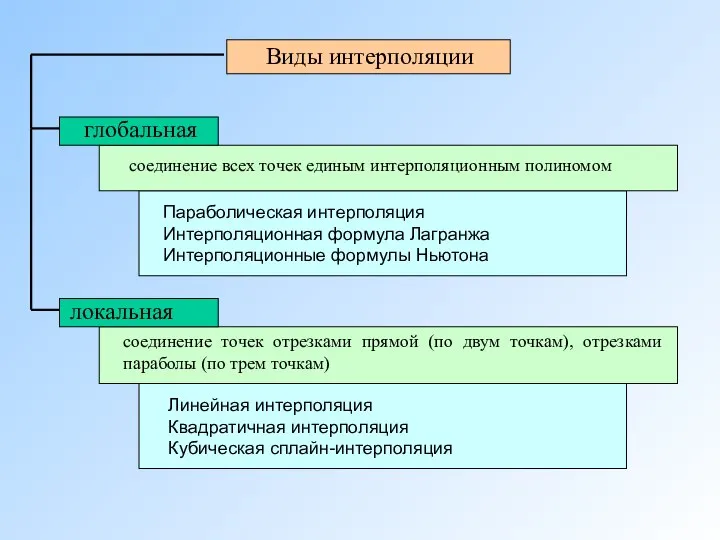
- 6. Виды интерполяции
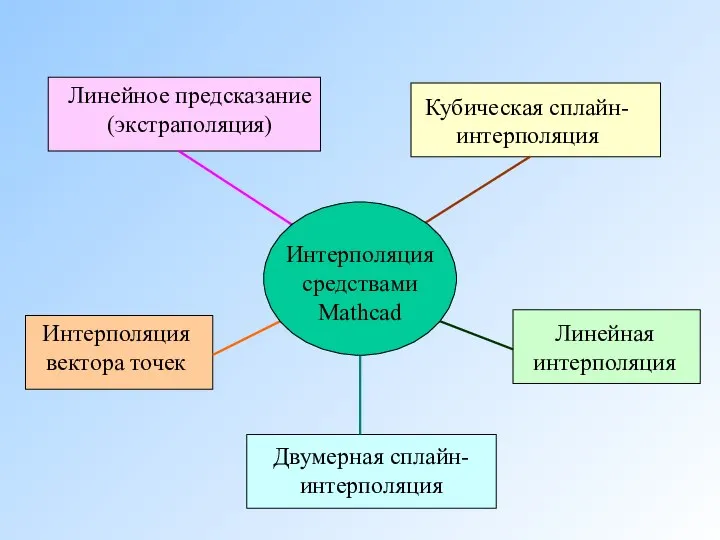
- 7. Интерполяция средствами Mathcad
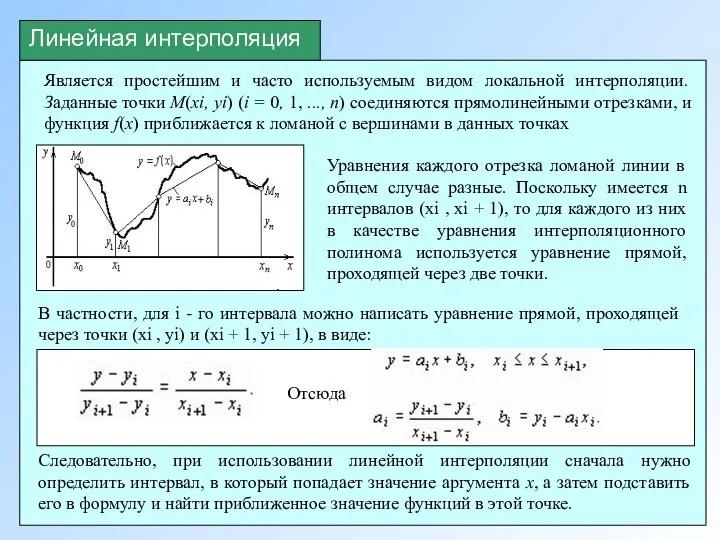
- 8. Является простейшим и часто используемым видом локальной интерполяции. Заданные точки М(xi, yi) (i = 0, 1,
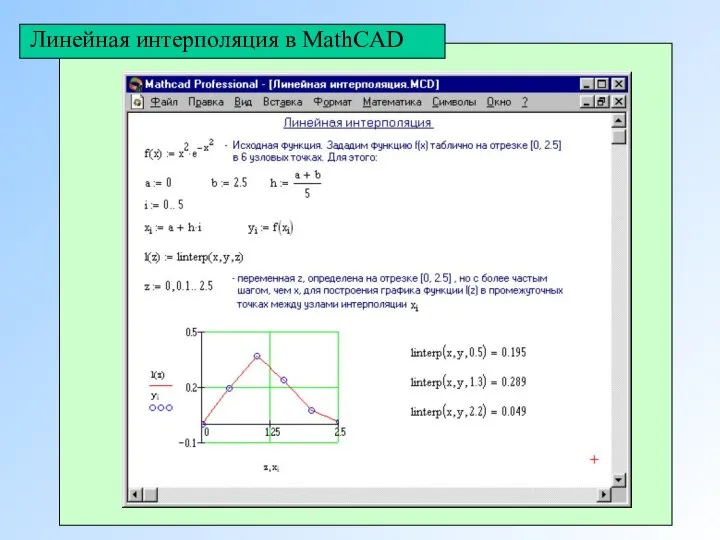
- 9. Линейная интерполяция в MathCAD При линейной интерполяции MathCAD соединяет существующие точки данных прямыми линиями (соединяет точки
- 10. Линейная интерполяция в MathCAD
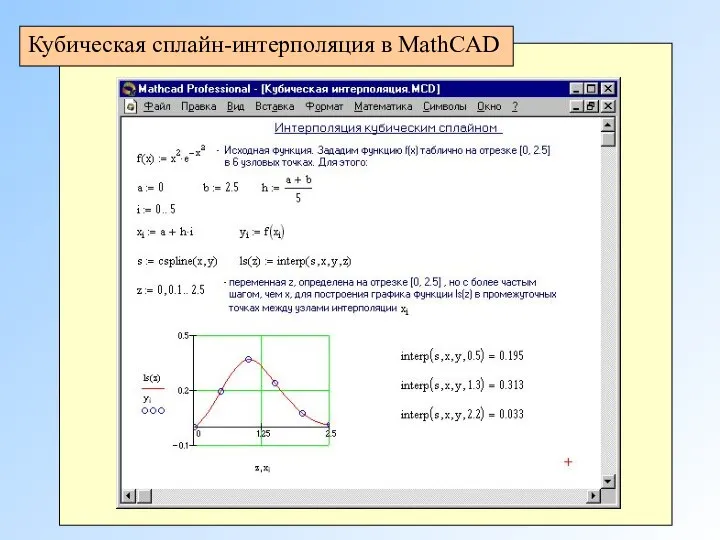
- 11. Наиболее широкое практическое применение, в силу их простоты, нашли кубические сплайны. Основные идеи теории кубических сплайнов
- 12. В общем случае для функции y = f(x) требуется найти приближение y = φ (x) таким
- 14. Кубическая сплайн-интерполяция в MathCAD Проводит кривую через набор точек таким образом, что первые и вторые производные
- 15. Построения кубического сплайна через набор точек: Создать векторы vx и vy, содержащие координаты x и y,
- 16. Кубическая сплайн-интерполяция в MathCAD
- 17. Можно использовать оператор векторизации, чтобы вычислить сразу целый набор интерполируемых значений, соответствую-щих вектору заданных точек. Это
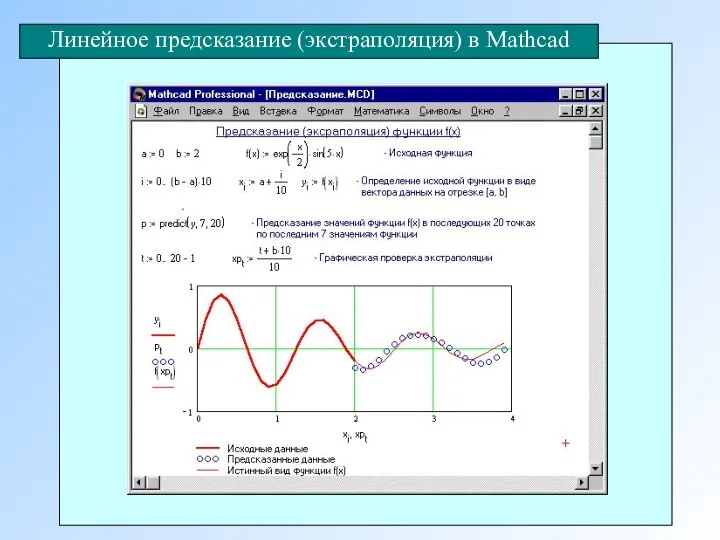
- 18. Функция predict В Mathcad позволяет оценить значения формул в точках, находящихся вне области расположения сетки, на
- 19. Линейное предсказание (экстраполяция) в Mathcad
- 20. Двумерная сплайн-интерполяция Используют для повышения качества построения 3D-графиков. Она позволяет существенно повысить представительность сложных графиков функций,
- 21. Построения двумерной сплайн-интерполяции Первый шаг точно такой же, как и в одномерном случае, но теперь нужно
- 23. Скачать презентацию
![На отрезке [a, b] заданы n + 1 точки xi =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1470003/slide-3.jpg)











 Анализ параллельных вычислений. Лекция 3
Анализ параллельных вычислений. Лекция 3 Полный курс подготовки к ЕГЭ по математике. Планиметрия. Углы, связанные с окружностью
Полный курс подготовки к ЕГЭ по математике. Планиметрия. Углы, связанные с окружностью Математические модели задач на движение или работу
Математические модели задач на движение или работу Алгебра логики
Алгебра логики Квадратичная функция. Ее свойства и график. Проверка домашнего задания
Квадратичная функция. Ее свойства и график. Проверка домашнего задания Выигрышная стратегия
Выигрышная стратегия Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Показательная и тригонометрические функции комплексного переменного
Показательная и тригонометрические функции комплексного переменного СКАЛЯРНОЕ ПРОЗВЕДЕНИЕ ВЕКТОРОВ Подготовили: Рощупкина Л.И., Воложанина Т.Н. урок математики 9 класс МБОУ СОШ №96 Г.Барнаул
СКАЛЯРНОЕ ПРОЗВЕДЕНИЕ ВЕКТОРОВ Подготовили: Рощупкина Л.И., Воложанина Т.Н. урок математики 9 класс МБОУ СОШ №96 Г.Барнаул  Число 10
Число 10 Вычитание из чисел 6 и 7. Состав 6 и 7
Вычитание из чисел 6 и 7. Состав 6 и 7 Сложение с переходом через десяток. Тренажёр
Сложение с переходом через десяток. Тренажёр Аттестационная работа. Проектная и исследовательская деятельность учащихся на уроках математики
Аттестационная работа. Проектная и исследовательская деятельность учащихся на уроках математики Вынужденные гармонические колебания стержней с распределенной массой при изгибе
Вынужденные гармонические колебания стержней с распределенной массой при изгибе Оптимизационные методы решения систем линейных алгебраических уравнений
Оптимизационные методы решения систем линейных алгебраических уравнений Размещение из N элементов по k (k ≤ n)
Размещение из N элементов по k (k ≤ n) Функция. График функции
Функция. График функции Перпендикулярность плоскостей. Параллелепипед
Перпендикулярность плоскостей. Параллелепипед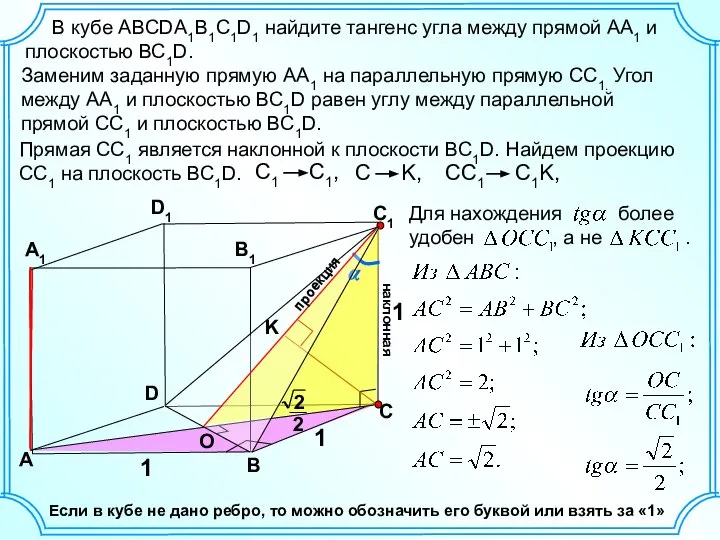 Задача 37
Задача 37 Разложение многочлена на множители
Разложение многочлена на множители Математический турнир
Математический турнир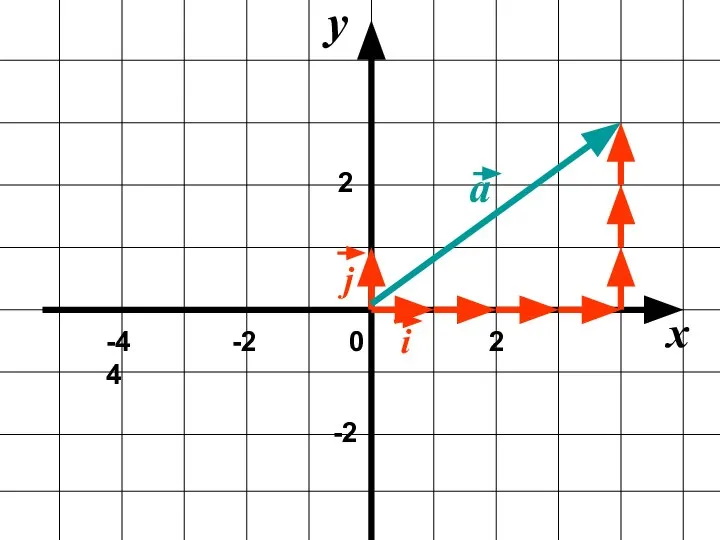 Координаты вектора
Координаты вектора Системы линейных уравнений Лекция 3
Системы линейных уравнений Лекция 3  Необходимый признак экстремума
Необходимый признак экстремума Areas of Prisms
Areas of Prisms Теория вероятностей
Теория вероятностей Четырехугольники. Трапеция
Четырехугольники. Трапеция Автор: Воронцова Ольга Владимировна
Автор: Воронцова Ольга Владимировна