Содержание
- 2. Общее уравнение поверхности второго порядка x, y, z − координаты точек поверхности − действительные числа.
- 3. Матричный вид уравнения поверхности второго порядка
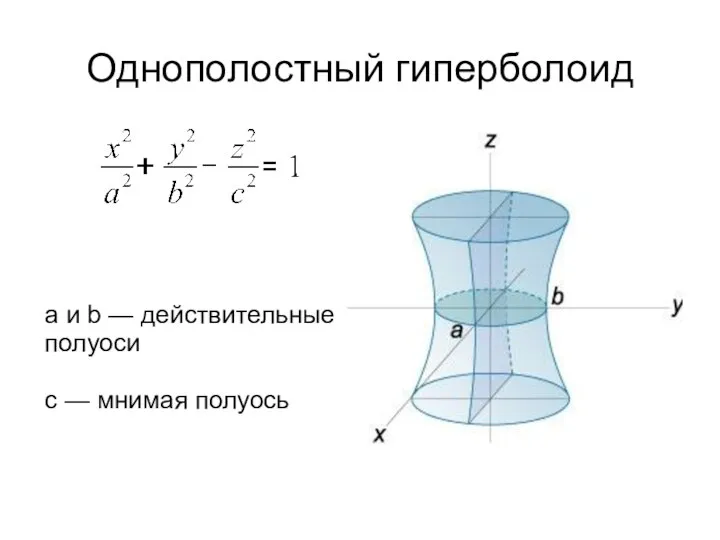
- 4. Однополостный гиперболоид a и b — действительные полуоси c — мнимая полуось
- 5. Свойства однополостного гиперболоида: 1. Однополостный гиперболоид - неограниченная поверхность, поскольку из его канонического уравнения следует, что
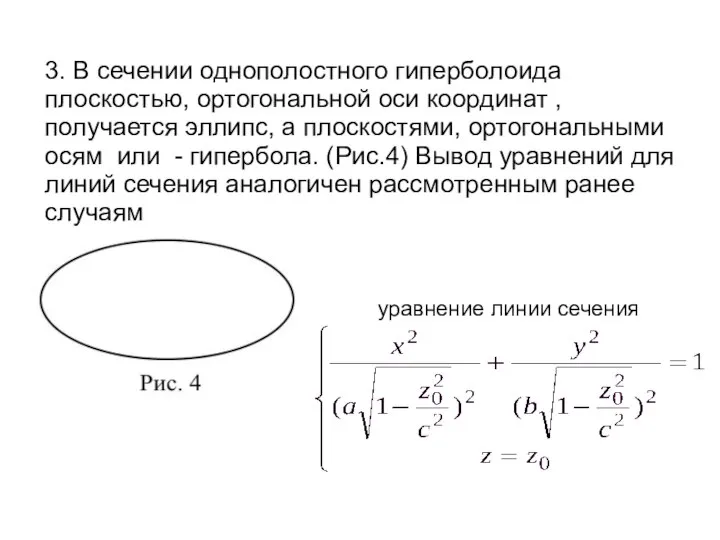
- 6. 3. В сечении однополостного гиперболоида плоскостью, ортогональной оси координат , получается эллипс, а плоскостями, ортогональными осям
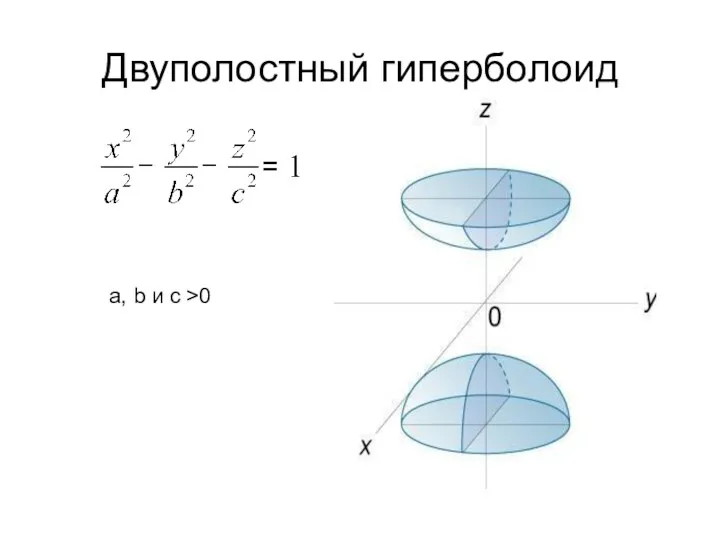
- 7. Двуполостный гиперболоид a, b и c >0
- 8. Свойства двуполостного гиперболоида: Двуполостный гиперболоид - неограниченная поверхность, поскольку из его канонического уравнения следует, что и
- 10. Скачать презентацию




 Приращение функции
Приращение функции Уравнения, приводимые к квадратным
Уравнения, приводимые к квадратным Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа Зимние забавы. Счет в пределах 10
Зимние забавы. Счет в пределах 10 Внеклассное мероприятие по геометрии в 8 классе
Внеклассное мероприятие по геометрии в 8 классе Квадратные корни
Квадратные корни Алгебраическая сумма и её свойства
Алгебраическая сумма и её свойства Графический способ решения уравнений
Графический способ решения уравнений Поворот. Фигуры вращения
Поворот. Фигуры вращения Вычитание.6 класс
Вычитание.6 класс Лемма. Параллельность трёх прямых
Лемма. Параллельность трёх прямых Готовимся к ВПР по математике
Готовимся к ВПР по математике Николаева Анна Дмитриевна учитель изо МОУ « СОШ п.Возрождение» Хвалынский район Саратовская область
Николаева Анна Дмитриевна учитель изо МОУ « СОШ п.Возрождение» Хвалынский район Саратовская область Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Методы математического моделирования в электронике. Основные понятия
Методы математического моделирования в электронике. Основные понятия Сложение и вычитание двузначных чисел
Сложение и вычитание двузначных чисел Авторы: Плышевская Л. Бубнова Е Кузнецова Е. Степанова К. – ученицы 8В класса г. Амур
Авторы: Плышевская Л. Бубнова Е Кузнецова Е. Степанова К. – ученицы 8В класса г. Амур Свойства прямоугольных треугольников. Решение задач на применение свойств прямоугольных треугольников
Свойства прямоугольных треугольников. Решение задач на применение свойств прямоугольных треугольников Определение первообразной
Определение первообразной Теорема о соотношениях между сторонами и углами треугольника
Теорема о соотношениях между сторонами и углами треугольника Двугранный угол (Урок геометрии в 10 классе)
Двугранный угол (Урок геометрии в 10 классе) Теория вероятностей
Теория вероятностей Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы
Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы Круги Эйлера
Круги Эйлера Последовательность комплексных чисел
Последовательность комплексных чисел Презентация по математике "Сложение и вычитание натуральных чисел" - скачать бесплатно
Презентация по математике "Сложение и вычитание натуральных чисел" - скачать бесплатно Многогранники
Многогранники История развития тригонометрии
История развития тригонометрии