Содержание
- 2. Линейная алгебра Система двух линейных уравнений с двумя неизвестными и понятие определителя 2-го порядка. Определители 3-го
- 3. Понятие определителя 2-го порядка Определитель второго порядка, соответствующий таблице элементов , определяется равенством где a1 и
- 4. Системы 2-х линейных уравнений с 2-мя неизвестными
- 5. Варианты решений Δ≠0– система имеет единственное решение - формулы Крамера Δ=0, Δx≠0, Δу ≠0, Δz ≠0-
- 6. Определители 3-го порядка, вычисление и свойства Определитель третьего порядка, соответствующий таблице элементов , определяется равенством a1
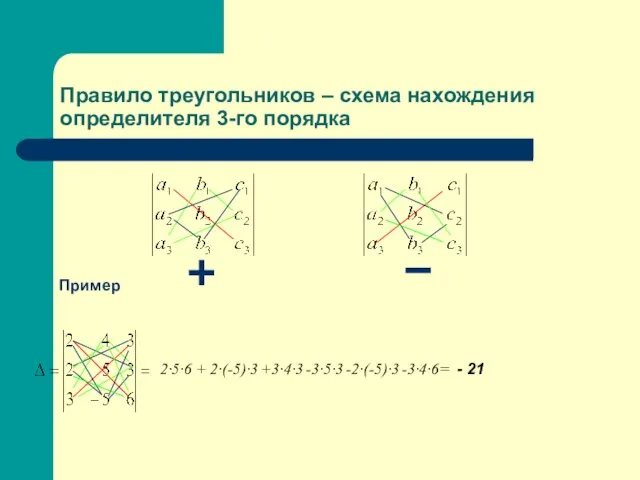
- 7. Правило треугольников – схема нахождения определителя 3-го порядка Пример 2∙5∙6 + 2∙(-5)∙3 +3∙4∙3 -3∙5∙3 -2∙(-5)∙3 -3∙4∙6=
- 8. Правило Саррюса- схема нахождения определителя 3-го порядка a1 b2 c3+ b1 c2 a3 + c1 a2
- 9. Свойства определителей Значение определителя не изменится, если строки определителя заменить столбцами, а столбцы – соответствующими строками.
- 10. Пример Вычислить определитель 3-го порядка Так как элементы 2-ой и 3-ей строки одинаковы, то определитель равен
- 11. Система двух линейных уравнений с тремя неизвестными. Если a1/a2=b1/b2=c1/c2, то система сводится к одному уравнению (например,
- 12. Правило Крамера – метод решения системы линейных уравнений
- 13. Варианты решений Δ≠0– система имеет единственное решение - формулы Крамера Δ=0, Δx≠0, Δу ≠0, Δz ≠0-
- 14. Пример: Решить систему линейных уравнений
- 15. Система трех однородных линейных уравнений с тремя неизвестными. Линейное уравнение называется однородным, если его свободный член
- 16. Понятие определителя n-го порядка.
- 17. Минором Мij элемента aij определителя n-го порядка называется определитель (n-1)-го порядка который получается путем вычеркивания в
- 18. Теорема Лапласа Каждый определитель равен сумме произведений элементов любой его строки(столбцов) на их алгебраические дополнения, т.е.
- 19. Пример: Вычислить определитель, разлагая его по элементам второго столбца
- 20. Пример: Вычислить определитель 4-го порядка Прибавим к первой строке удвоенную третью, ко второй строке -третью, умноженную
- 21. Обобщение формулы Крамера на случай системы n - линейных уравнений. Из коэффициентов при неизвестных составим определитель,
- 22. Варианты решений Если для системы уравнений определитель Δ≠0, то система имеет единственное решение где определитель Δi
- 23. Пример: Решить систему линейных уравнений Вычислим определитель системы
- 24. Поскольку ∆ ≠ 0, система уравнений может быть решена по формулам Крамера. Найдем определители ∆x1 –
- 25. Таким же образом высчитываем ∆х4 и получаем: ∆х1 = ∆х2 = –∆х3 = ∆х4, и, следовательно,
- 26. Понятие матрицы. Линейные операции над матрицами или, в сокращенной записи, А=(аij); i=1, 2, ..., m; j
- 27. Виды матриц Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е.
- 28. Виды матриц Матрица получающаяся из матрицы A заменой строк столбцами (и наоборот), называется транспонированной (по отношению
- 29. Линейные операции над матрицами. Умножением матрицы на число k называется матрица, каждый элемент которой умножен на
- 30. Обратная матрица
- 31. Теорема (необходимое и достаточное условие существования обратной матрицы).
- 32. Пример: Найти матрицу, обратную к матрице
- 33. Пример: Найти матрицу, обратную матрице А= Найдем определитель исходной матрицы: ∆А= Так как ∆А = 0,
- 34. Решение системы линейных уравнений методом обратной матрицы
- 35. Пример: Решить систему уравнений
- 36. Ранг матрицы.
- 37. Методы вычисления ранга матрицы - метод окаймляющих миноров
- 38. Пример: Найти ранг матрицы
- 39. Совместность систем уравнений. Теорема Кронеккера-Капелли.
- 40. Пример: Установить совместимость системы
- 42. Скачать презентацию






































 Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения Элементы векторной алгебры (лекция № 2)
Элементы векторной алгебры (лекция № 2) Геометрические приложения определенного интеграла
Геометрические приложения определенного интеграла Теорема обратная теореме Пифагора
Теорема обратная теореме Пифагора Логика предикатов
Логика предикатов Прямоугольный треугольник
Прямоугольный треугольник  Алгебра высказываний
Алгебра высказываний Понятие объема многогранников. Объем прямоугольного параллелепипеда.
Понятие объема многогранников. Объем прямоугольного параллелепипеда. Алгебра. Многочлены. Урок 2-9
Алгебра. Многочлены. Урок 2-9 Свойства площадей многоугольника. (8 класс)
Свойства площадей многоугольника. (8 класс) Первообразная и интеграл
Первообразная и интеграл Решение уравнений (урок 3). 6 класс
Решение уравнений (урок 3). 6 класс Задание 9: вычисления и преобразования
Задание 9: вычисления и преобразования Вычисление дробей
Вычисление дробей Аттестационная работа. Образовательная программа курса по математике Методы решения уравнений, неравенств и их систем
Аттестационная работа. Образовательная программа курса по математике Методы решения уравнений, неравенств и их систем Пропорциональное деление
Пропорциональное деление Путешествие на остров натуральных чисел
Путешествие на остров натуральных чисел Аттестационная работа. Образовательная программа внеурочной деятельности «Решение олимпиадных задач по математике»
Аттестационная работа. Образовательная программа внеурочной деятельности «Решение олимпиадных задач по математике» Знаки Больше, меньше, равно
Знаки Больше, меньше, равно Магические квадраты
Магические квадраты Презентация на тему Решение логарифмических уравнений
Презентация на тему Решение логарифмических уравнений Ментальная арифметика. Программа для развития ребенка
Ментальная арифметика. Программа для развития ребенка Теорема Пифагора
Теорема Пифагора Физический (механический) смысл производной
Физический (механический) смысл производной Число Пи
Число Пи Функция и её график
Функция и её график Одночлен. 7 класс
Одночлен. 7 класс 20161212_ot_evklida_do_lobachevskogo
20161212_ot_evklida_do_lobachevskogo