Содержание
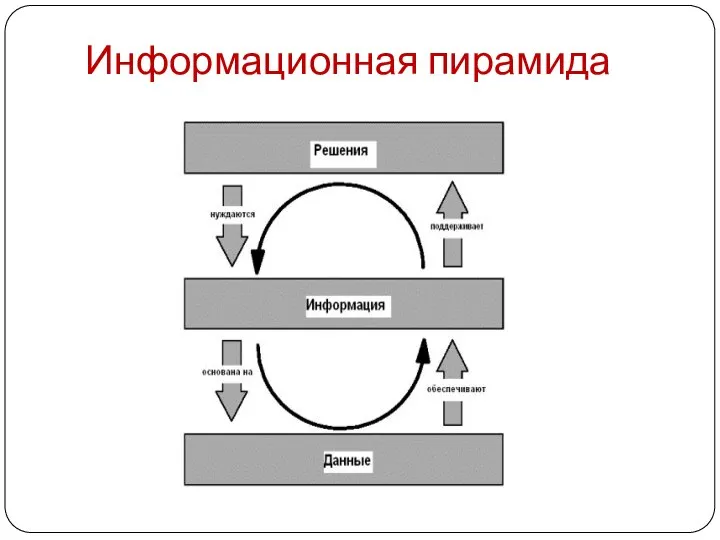
- 2. Информационная пирамида
- 3. Методы анализа данных Статистические: Дескриптивный анализ. Анализ природы данных (проверка гипотез стационарности, нормальности, однородности, оценка вида
- 4. Генеральная и выборочная совокупности Генеральная совокупность - вся совокупность изучаемых объектов, интересующая исследователя. Выборка - часть
- 5. 1. Номинальная шкала 2. Порядковая шкала 3. Интервальная шкала 4. Относительная шкала 5. Дихотомическая шкала Виды
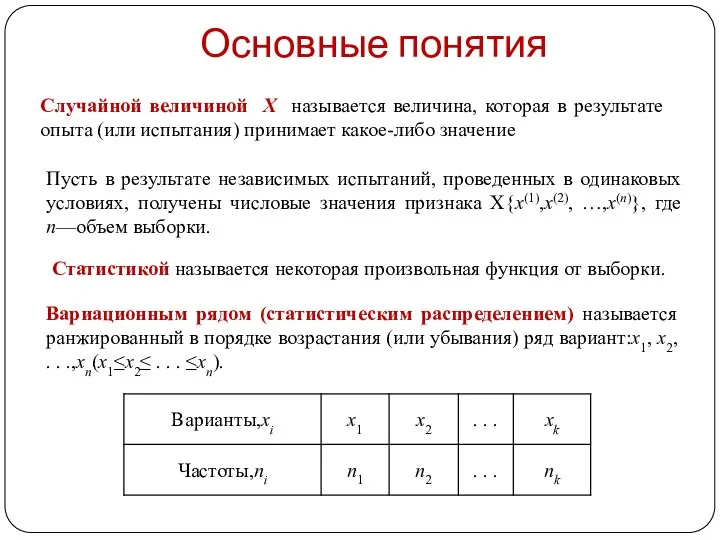
- 6. Статистикой называется некоторая произвольная функция от выборки. Случайной величиной X называется величина, которая в результате опыта
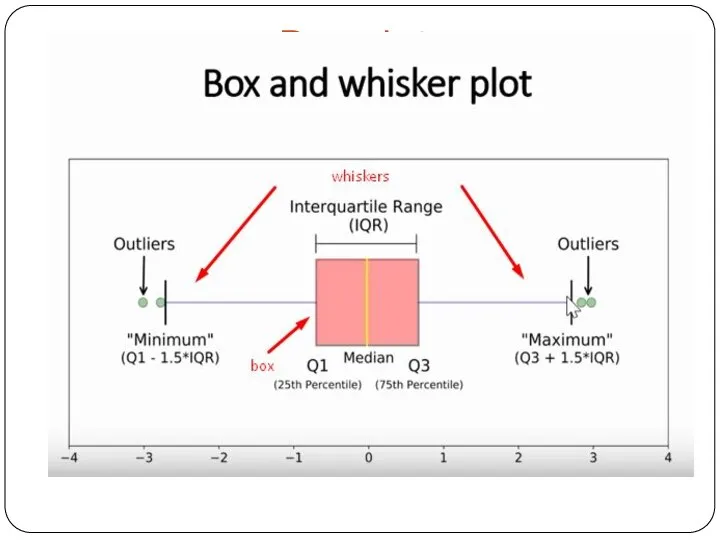
- 7. Выбросы. Квартили Межквартильный размах (IQR) — это разность между третьим и первым квартилем. Выброс — это
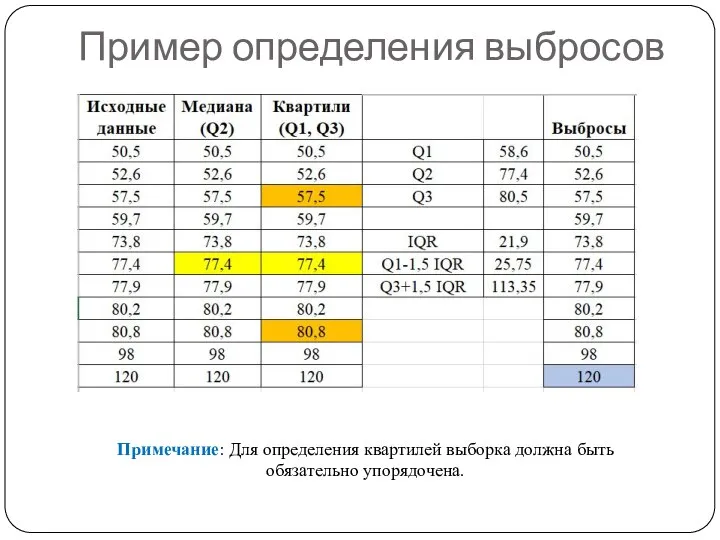
- 8. Пример определения выбросов Примечание: Для определения квартилей выборка должна быть обязательно упорядочена.
- 9. Интервальный вариационный ряд 1. Вычисляют размах R варьирования признака Х как разность между наибольшим xmax и
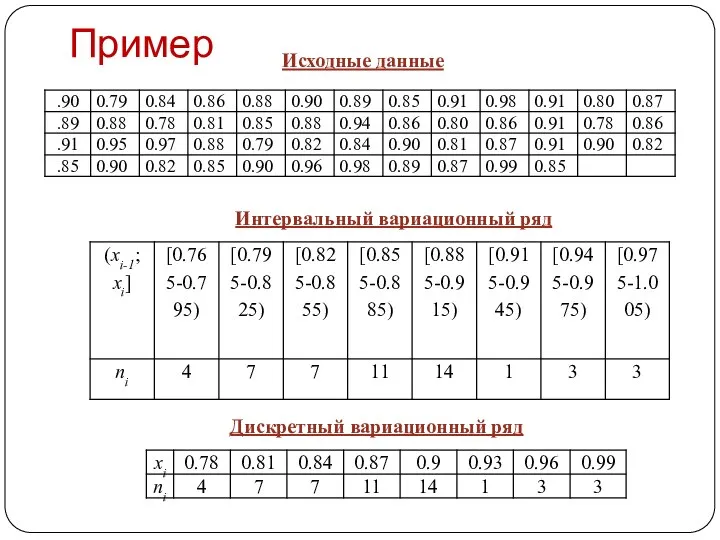
- 10. Пример Исходные данные Интервальный вариационный ряд Дискретный вариационный ряд
- 11. Построение интервального вариационного ряда 1. Рассчитаем размах варьирования: где xmin – наименьшая варианта данной выборочной совокупности;
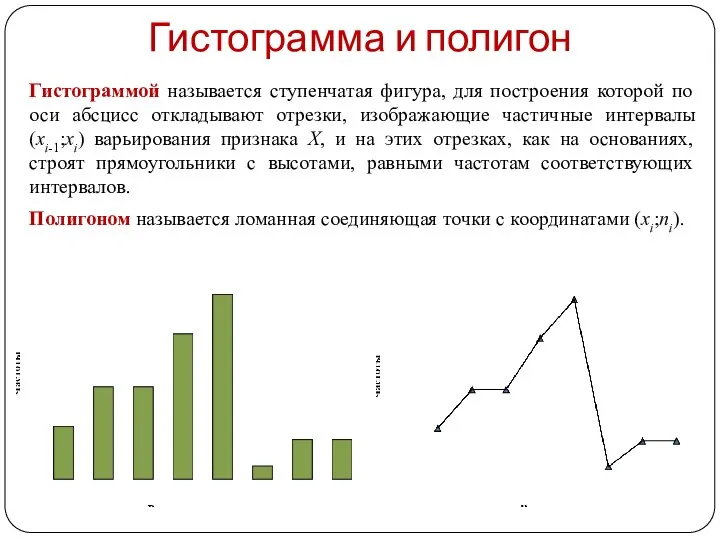
- 12. Гистограмма и полигон Гистограммой называется ступенчатая фигура, для построения которой по оси абсцисс откладывают отрезки, изображающие
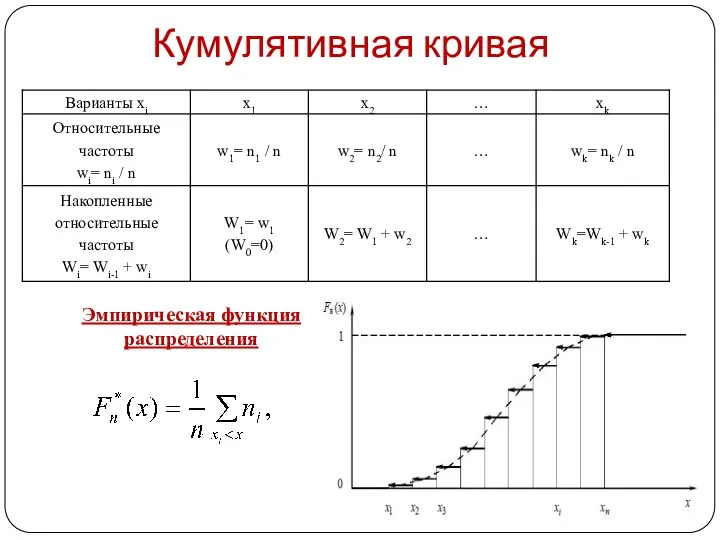
- 13. Кумулятивная кривая Эмпирическая функция распределения .
- 14. Центральная тенденция Выборочная средняя Примечание: При анализе данных средним не следует злоупотреблять, необходимо учитывать его свойства
- 15. Центральная тенденция Медианой Me называют варианту которая делит вариационный ряд на две равные по числу вариант
- 16. Центральная тенденция Модой Mo называют варианту, которая имеет наибольшую частоту. Коэффициент вариации - меры разброса признака
- 17. Дисперсия Если объем выборки n>50, то рассчитывают исправленную дисперсию: Формула расчета дисперсии для несгруппированных данных Формула
- 18. Box plot
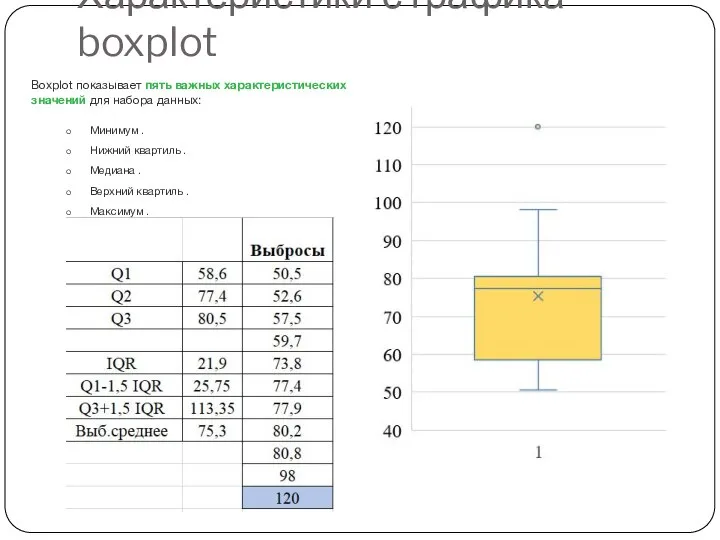
- 19. Характеристики с графика boxplot Boxplot показывает пять важных характеристических значений для набора данных: Минимум . Нижний
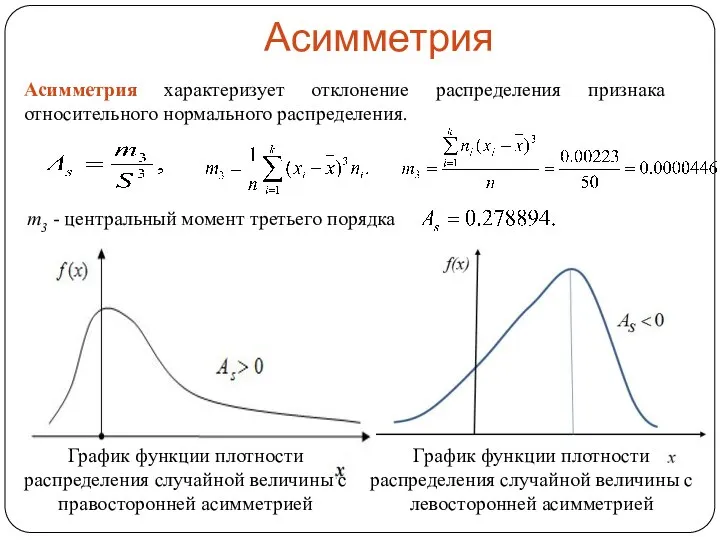
- 20. Асимметрия Асимметрия характеризует отклонение распределения признака относительного нормального распределения. m3 - центральный момент третьего порядка График
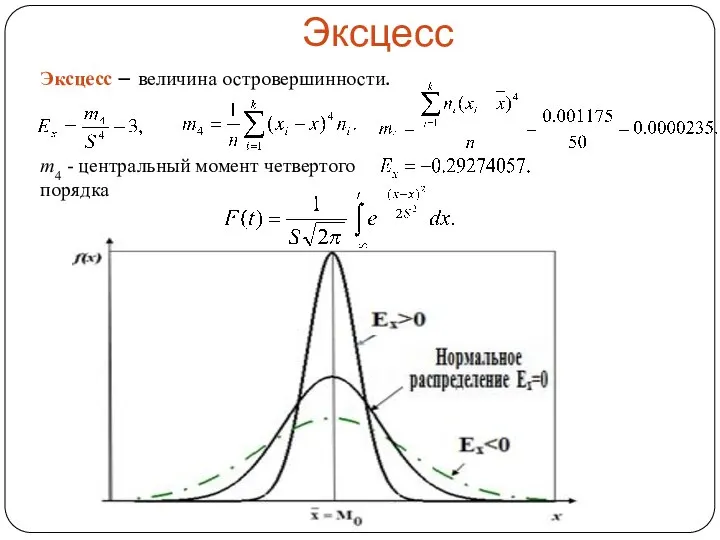
- 21. Эксцесс Эксцесс – величина островершинности. m4 - центральный момент четвертого порядка
- 22. Доверительные интервалы Для математического ожидания Для дисперсии где, -γ-квантиль распределения Стьюдента с n-1 степенью свободы. Примечание:
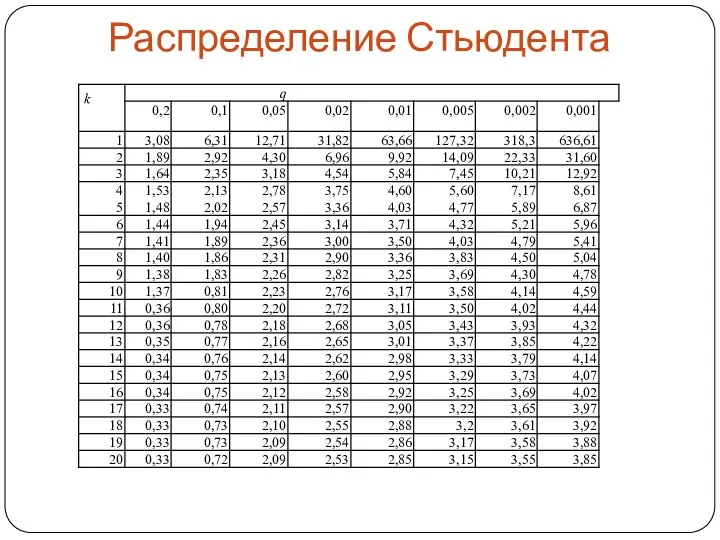
- 23. Распределение Стьюдента
- 25. Скачать презентацию











 Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс
Урок математики «Закрепление письменных приемов сложения и вычитания» Учитель: Циндяйкина С. А. 2 класс Расстояние от точки до прямой
Расстояние от точки до прямой Теорема Пифагора. Обратная теорема теореме Пифагора
Теорема Пифагора. Обратная теорема теореме Пифагора Алгоритм Евклида для нахождения НОД. Малая теорема Ферма. Функция Эйлера (Лекция 5)
Алгоритм Евклида для нахождения НОД. Малая теорема Ферма. Функция Эйлера (Лекция 5) Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс
Внеклассное мероприятие по математике с элементами экономики. В отделении Сбербанка. 5 класс Математична модель оцінювання сталого розвитку
Математична модель оцінювання сталого розвитку Презентация по математике "Различные подходы к доказательству теоремы Пифагора" - скачать
Презентация по математике "Различные подходы к доказательству теоремы Пифагора" - скачать  Треугольник. Углы
Треугольник. Углы Задачи на координатной плоскости
Задачи на координатной плоскости Интерактивный тренажёр «В стране Математики». 1 класс
Интерактивный тренажёр «В стране Математики». 1 класс Операции на нечетких множествах
Операции на нечетких множествах Тема урока: «Числа от 1 до 100. Письменные вычисления»
Тема урока: «Числа от 1 до 100. Письменные вычисления»  Метод резолюций в исчислении предикатов
Метод резолюций в исчислении предикатов Преобразование переменных в парной регрессии
Преобразование переменных в парной регрессии Второй признак равенства треугольников
Второй признак равенства треугольников Тренажер Теремок. Состав чисел первого десятка
Тренажер Теремок. Состав чисел первого десятка Лекция №8 Двойные интегралы
Лекция №8 Двойные интегралы Сравнение отрезков и углов. Биссектриса угла
Сравнение отрезков и углов. Биссектриса угла Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия
Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия Сказка
Сказка Типы случайных событий и действия над ними. Теория вероятностей
Типы случайных событий и действия над ними. Теория вероятностей Презентация на тему Линии пересекающиеся и непересекающиеся» УМК
Презентация на тему Линии пересекающиеся и непересекающиеся» УМК  Женщины-математики.
Женщины-математики. Окружность. Отличие круга от окружности
Окружность. Отличие круга от окружности Действия с положительными и отрицательными числами
Действия с положительными и отрицательными числами Решение систем линейных алгебраических уравнений. Тема 3
Решение систем линейных алгебраических уравнений. Тема 3 Многогранник пирамида
Многогранник пирамида Неравенства. Знаки «< », «>»
Неравенства. Знаки «< », «>»