Теорема Пифагора в древнейшем китайском трактате «Чжоу-би»
Теорема Пифагора упоминается в первой
части самого древнего дошедшего до нас китайского математико-астрономического сочинения «Чжоу-би», написанного около 1100 лет до н.э.
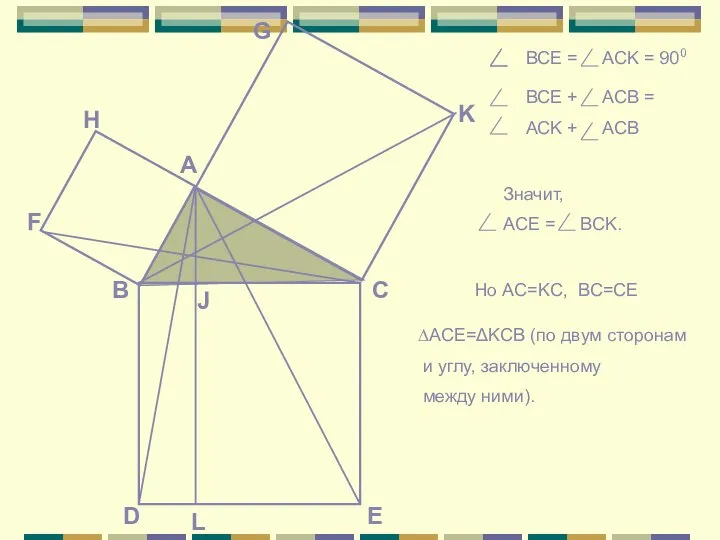
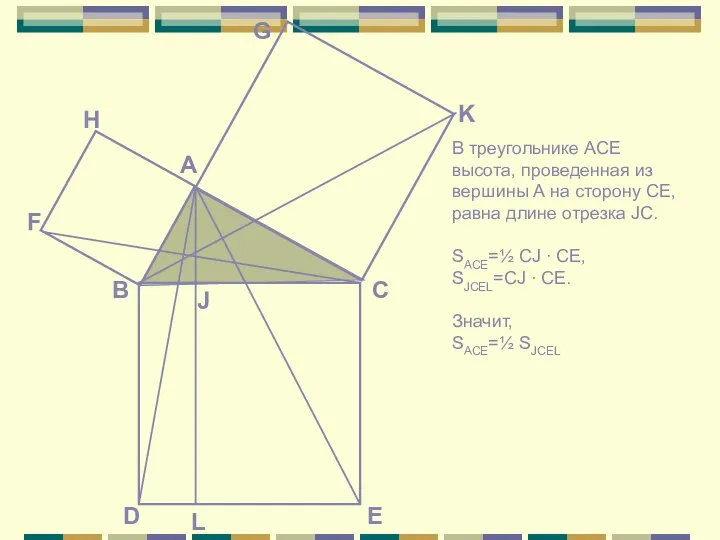
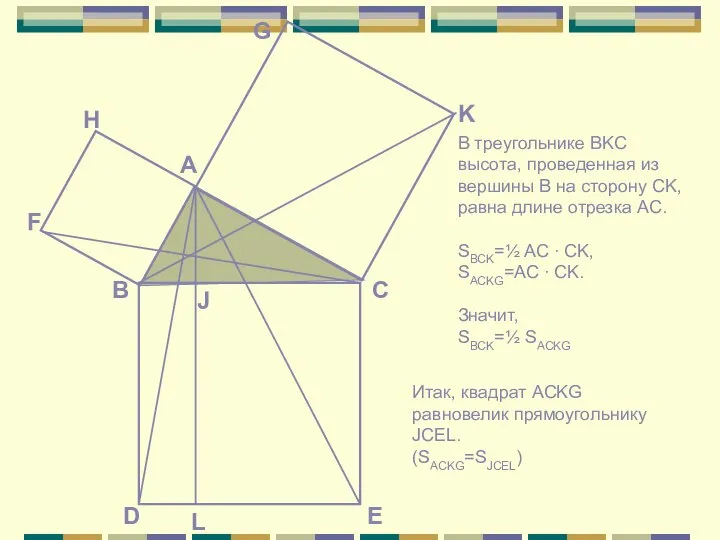
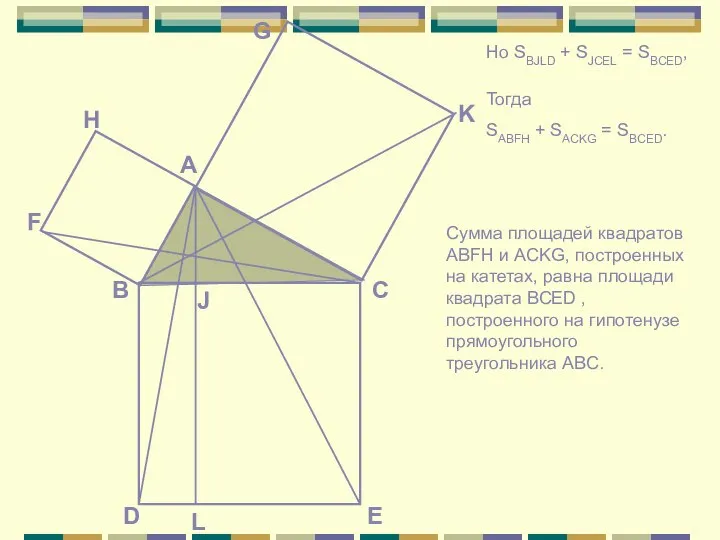
Прокл в своем комментарии к «Началам» Евклида пишет относительно предложения о том, что квадрат гипотенузы равен сумме квадратов катетов, следующее: «Если слушать тех, кто любит повторять древние легенды, то придется сказать, что эта теорема восходит к Пифагору. Рассказывают, что в честь этого открытия он принес в жертву быка». О том же рассказывает и другой греческий историк древности – Плутарх (I в.). На основе этих и других преданий долгое время считали, что до Пифагора эта теорема не была известна и назвали ее поэтому «теоремой Пифагора»…
Однако теперь известно, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.


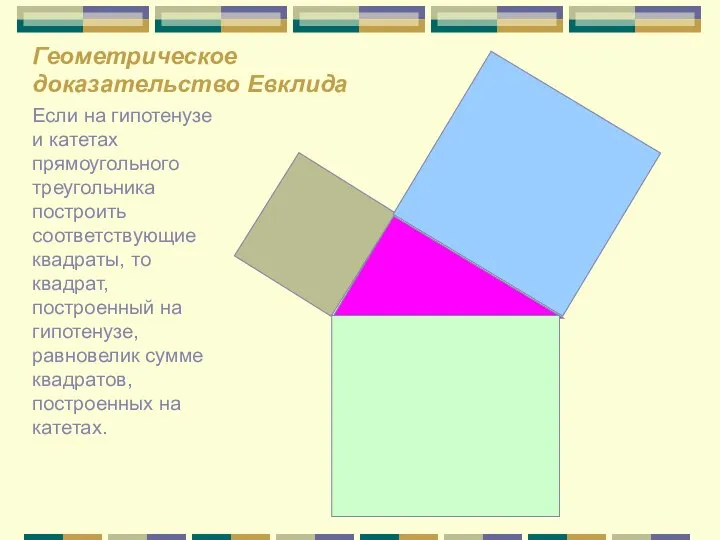
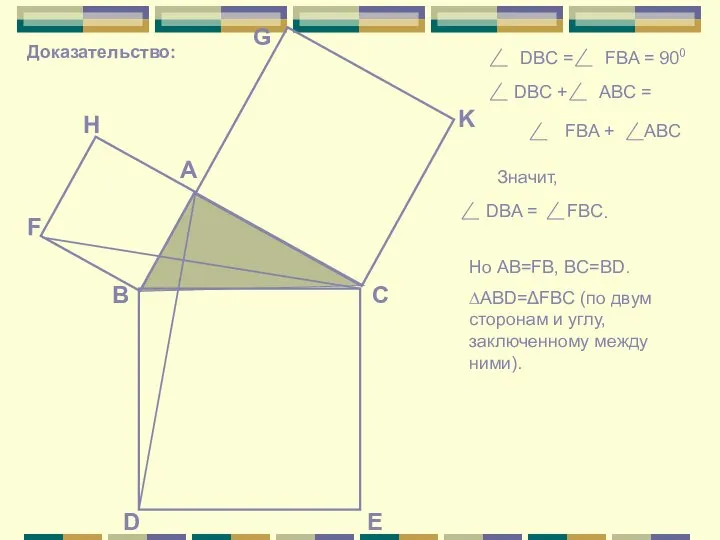
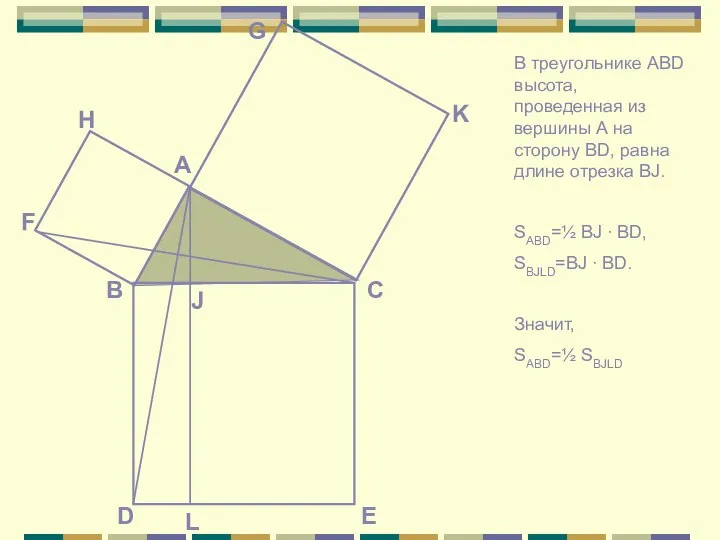
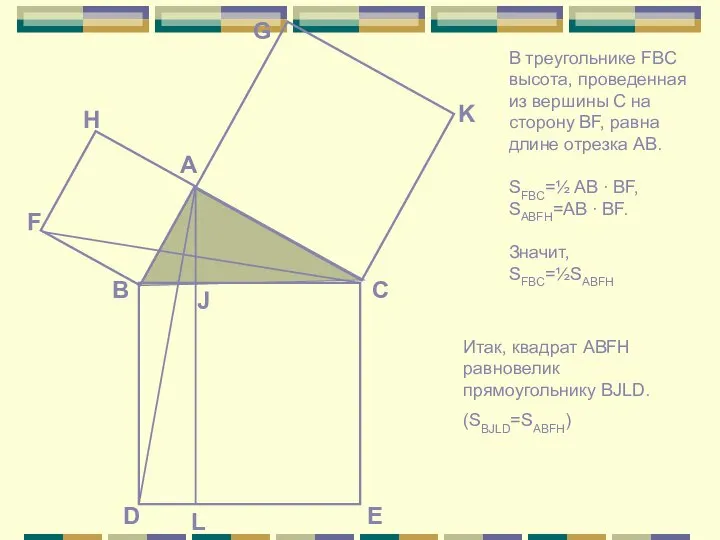


 Математическая логика
Математическая логика Презентация по математике "Путешествие на планету "Математика"" - скачать
Презентация по математике "Путешествие на планету "Математика"" - скачать  Geometrický význam integrálu
Geometrický význam integrálu Проценты. 5 класс
Проценты. 5 класс Математическая разминка
Математическая разминка Элементарные функции. Гиперболические тангенс и котангенс
Элементарные функции. Гиперболические тангенс и котангенс Измерение высоты предмета
Измерение высоты предмета  Одночлен и его стандартный вид
Одночлен и его стандартный вид Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Теория массового обслуживания
Теория массового обслуживания Основы теории ошибок измерений
Основы теории ошибок измерений Свойства числовых неравенств
Свойства числовых неравенств Интегрирование функции одной переменной
Интегрирование функции одной переменной Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Делимость двучленов
Делимость двучленов Визначення площі многокутника
Визначення площі многокутника Всё про углы
Всё про углы Эконометрическая модель и её спецификация
Эконометрическая модель и её спецификация Подготовка к выполнению заданий С2 ЕГЭ по математике
Подготовка к выполнению заданий С2 ЕГЭ по математике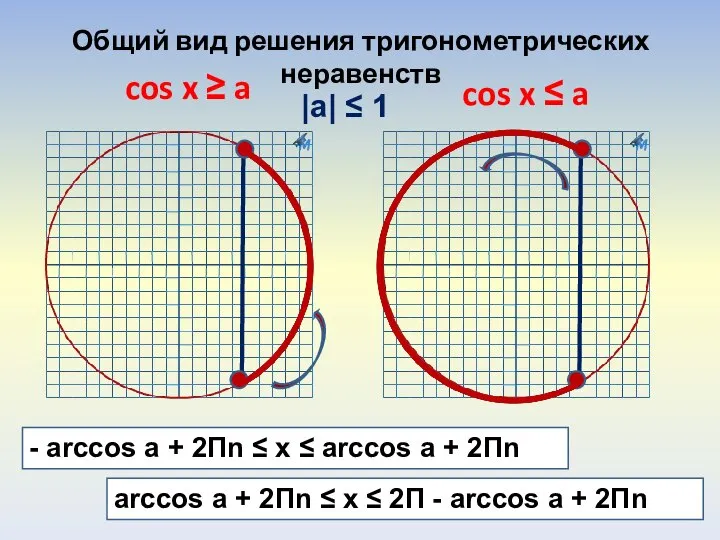 Общий вид решения тригонометрических неравенств
Общий вид решения тригонометрических неравенств Устный счёт по математике (2 класс) - презентация_
Устный счёт по математике (2 класс) - презентация_ Связь между координатами векторов и координатами точек
Связь между координатами векторов и координатами точек Логарифм. Основные свойства логарифмов
Логарифм. Основные свойства логарифмов Вынесение множителя из-под знака корня. Внесение множителя под знак корня
Вынесение множителя из-под знака корня. Внесение множителя под знак корня Алгебраические выражения
Алгебраические выражения Применение разноуровневого обучения на уроках математики Путинцева Любовь Алексеевна
Применение разноуровневого обучения на уроках математики Путинцева Любовь Алексеевна Урок з математики у 2 класі
Урок з математики у 2 класі Технология проблемного обучения на примерах уроков разных типов. Деление обыкновенных дробей. 6 класс
Технология проблемного обучения на примерах уроков разных типов. Деление обыкновенных дробей. 6 класс