Содержание
- 2. Определение: Примеры: – множество автомобилей на улице; – множество букв алфавита; – множество чисел. Множество –
- 3. Основное понятие: Обозначение множеств: Принадлежность – является ли некоторый объект элементом множества. Множества Элементы теории множеств
- 4. Сравнение множеств: Объединение множеств: Объединением множеств А и В называется такое множество Множества А и В
- 5. Пересечение множеств: Вычитание множеств: Операции над множествами Элементы теории множеств Пересечением множеств А и В называется
- 6. Подмножество: Операции над множествами Элементы теории множеств Если любой элемент множества А принадлежит множеству Е, то
- 7. Определение: Под действительным числом будем понимать такое число, которое мы можем записать и сопоставить некоторому реальному
- 8. Свойство упорядоченности: Если а и b – произвольные действительные числа, то: либо a = b, либо
- 9. Определение: Модулем или абсолютной величиной действительного числа называется неотрицательное число, определяемое так: Модуль действительного числа Автор:
- 10. Определение 1: Окрестностью точки x = a радиусом ε > 0 (или ε-окрестностью) называется множество действительных
- 11. Множество действительных чисел может быть дополнено двумя элементами: Бесконечность Автор: И. В. Дайняк, к.т.н., доцент Кафедра
- 12. Множество действительных чисел может быть дополнено двумя элементами: Бесконечность Автор: И. В. Дайняк, к.т.н., доцент Кафедра
- 13. Целые числа: Если к множеству натуральных чисел добавить противоположные по знаку числа и число «нуль», то
- 14. Иррациональные числа: Дробные числа, которые не могут быть представлены в виде Множество иррациональных чисел обозначается J.
- 15. Математические символы: Кванторы Обозначение: Значение: «существует», «найдётся». Элементы математической логики Квантор существования: Обозначение: Значение: «всякий», «каждый»,
- 16. Высказывания Высказывание – повествовательное предложение, в отношении которого можно сказать, истинно оно или ложно. Элементы математической
- 17. Аксиомы и теоремы Элементы математической логики Доказательство теоремы: Аксиома – математическое утверждение, истинность которого принимается без
- 19. Скачать презентацию
















 Визуализация операций над эллиптическими кривыми
Визуализация операций над эллиптическими кривыми Прикладное применение подобия треугольников
Прикладное применение подобия треугольников Методические особенности школьного курса математики. (5-6 класс)
Методические особенности школьного курса математики. (5-6 класс) Математическая логика
Математическая логика Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Определение подобных треугольников
Определение подобных треугольников Застосування відсотків у життєдіяльності людини
Застосування відсотків у життєдіяльності людини Моделирование зависимостей между величинами
Моделирование зависимостей между величинами Угол между плоскостями. Задание 13
Угол между плоскостями. Задание 13 Определители. Свойство определителей
Определители. Свойство определителей Статистический анализ случайных погрешностей
Статистический анализ случайных погрешностей Системы линейных уравнений. Метод Гаусса
Системы линейных уравнений. Метод Гаусса Математика. Расписание экзаменов
Математика. Расписание экзаменов МБОУ «Пригородная средняя общеобразовательная школа №1 Оренбургского района» Из истории обыкновенных дробей Работа учащегося
МБОУ «Пригородная средняя общеобразовательная школа №1 Оренбургского района» Из истории обыкновенных дробей Работа учащегося  Статистические характеристики
Статистические характеристики Презентация по математике "Софизмы" - скачать
Презентация по математике "Софизмы" - скачать  Подготовка к ВПР (№1). Математика 6 класс
Подготовка к ВПР (№1). Математика 6 класс Тема урока: Взаимно обратные числа
Тема урока: Взаимно обратные числа Теоретическая модель жизни пчелиных колоний
Теоретическая модель жизни пчелиных колоний Деление натуральных чисел. 5 класс
Деление натуральных чисел. 5 класс Движения
Движения Живаева Екатерина Ученица 11 класса
Живаева Екатерина Ученица 11 класса МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ
МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ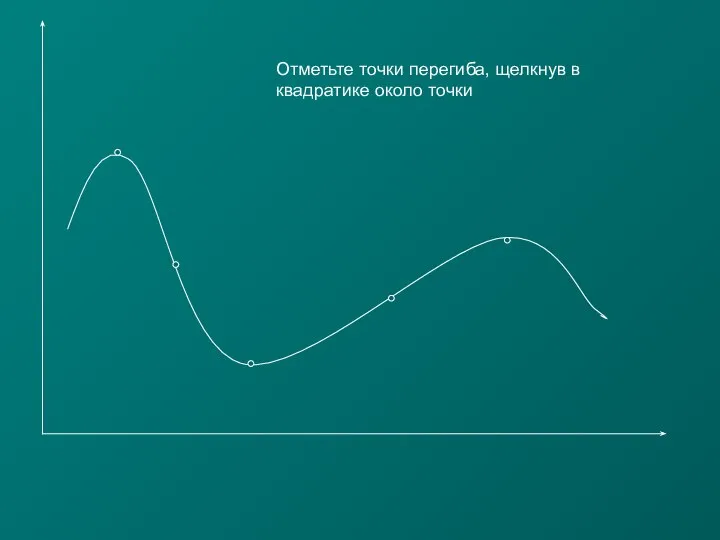 Точки перегиба
Точки перегиба Упрощение выражений. 5 класс
Упрощение выражений. 5 класс Математические диктанты. 2 класс
Математические диктанты. 2 класс Неравенство треугольника
Неравенство треугольника В8 подготовка к ЕГЭ
В8 подготовка к ЕГЭ