Содержание
- 2. Содержание Закон Бера Основная задача РКТ Интегральное (прямое) преобразование Радона Методы обращения интегрального преобразования Радона: Метод
- 3. Закон Бера Известно, что всякая прямая может быть описана уравнением: xcosΘ + ysinΘ – s =
- 4. Преобразование Радона Преобразование Радона
- 5. Интегральное преобразование Радона Интенсивность излучения, прошедшего сквозь объект Проекцией p(ξ,θ) называется следующее соотношение: Используя свойства δ-функции
- 6. Пример №1. Вычислим радоновский образ двух распределений Гаусса Используя выражение (1.7) получим интегральное преобразование Радона R(s,φ)
- 7. Основная задача РКТ Восстановление неизвестной (искомой) функции µ(x,y) по измеренному набору проекций p(ξ,θ), связанных с искомой
- 8. Обратное преобразование Радона В фигурных скобках представлен несобственный интеграл по ξ, являющийся преобразованием Гильберта (Н) Интегрирование
- 9. Недостатки обратного преобразования Радона Формула обратного преобразования Радона весьма чувствительна к следующим погрешностям реальных измерений: Функцию
- 10. Более эффективные алгоритмы обращения, используемые в практической рентгеновской вычислительной томографии МЕТОДЫ ОБРАЩЕНИЯ ИНТЕГРАЛЬНОГО ПРЕОБРАЗОВАНИЯ РАДОНА АЛГЕБРАИЧЕСКИЕ
- 11. Состоит из двух этапов: Получение суммарного изображения g(x,y) с помощью операции обратного проецирования; Двумерная фильтрация суммарного
- 12. Обратное проецирование Операция обратного проецирования позволяет получить первое приближение к искомому решению g(x,y) , которое может
- 13. Обратное проецирование Рис. 5. Схема алгоритма обратного проецирования: (а) - получение проекций; (б) - суммирование обратных
- 14. Обратное проецирование Суммарное изображение g(x,y) связано с искомой функцией µ(x,y) уравнением свёртки: ρ-фильтрация
- 15. Суммарное изображение g(x,y) связано с искомой функцией µ(x,y) уравнением свёртки: Можно показать, что ядро двумерной свёртки
- 16. Вместо истинного значения µ(x,y) используется оценка истинного распределения по следующим причинам: При измерениях проекции p(ξ,θ) определяются
- 17. Двумерная фильтрация суммарного изображения Вычислим фурье-образ ядра Н2(u,v) в полярной системе координат. Ядро свёртки h2(x,y) в
- 18. Аподизирующая функция в виде прямоугольного импульса, ограниченного по полосе частот. ρ-фильтрация Косинусная аподизирующая функция Синусная аподизирующая
- 19. Обобщённая функция Хемминга ρ-фильтрация
- 20. 2. Метод Фурье-синтеза Данный метод обращения преобразования Радона основан на так называемой теореме о центральном сечении,
- 21. Таким образом, из одномерных фурье-образов проекций Р(ρ, ψ) можно набрать (синтезировать) двумерный фурье-образ искомого изображения М(ρ,
- 22. Таким образом, метод фурье-синтеза включает в себя следующую последовательность действий: Одномерное быстрое преобразование Фурье Интерполяция данных
- 23. 3. Метод одномерной фильтрации (метод фильтрованных обратных проекций) Последовательность действий в данном методе: Одномерная фильтрация каждой
- 24. Можно показать, что функция ядра свертки в Фурье-пространстве Н1(χ) имеет вид: и получить суммарное изображение ,
- 25. В качестве аподизирующих функций используют те же функции, что и в методе ρ-фильтрации. Рассмотрим, например, аподизирующую
- 26. Метод ФОП Согласно теореме Котельникова, если непрерывная функция f(x) имеет фурье-образ, отличный от нуля только на
- 27. Тогда выражение для отфильтрованной дискретной обратной проекции f(n·Δξ, θ) будет иметь следующий вид: Метод ФОП
- 28. Связь между числом радиальных Nξ и угловых Nθ отсчётов. Пусть Н – диаметр объекта исследования. Число
- 29. При равномерной выборке данных изображения угол проекции, выраженный в радианах, изменяется с шагом: При числе отсчётов
- 31. Скачать презентацию




























 НПВС-гастропатия. Эрозивно-язвенные поражения гастродуоденальной области
НПВС-гастропатия. Эрозивно-язвенные поражения гастродуоденальной области Роль антигистаминных препаратов в лечении и профилактике различных аллергических заболеваний
Роль антигистаминных препаратов в лечении и профилактике различных аллергических заболеваний Бұзау колибактериозының алдын алуы
Бұзау колибактериозының алдын алуы Влияние физических и умственных нагрузок на сердечно-сосудистую систему (сердце)
Влияние физических и умственных нагрузок на сердечно-сосудистую систему (сердце) Индивидуальный проект на тему: Контактные линзы или очки?
Индивидуальный проект на тему: Контактные линзы или очки? Стандартные операционные процедуры
Стандартные операционные процедуры СПИД - смертельная угроза человечества
СПИД - смертельная угроза человечества Учение об инфекционном процессе
Учение об инфекционном процессе Условия и факторы нормального и аномального развития личности
Условия и факторы нормального и аномального развития личности Подагра. Клинический разбор пациентки
Подагра. Клинический разбор пациентки Патология органов речи
Патология органов речи Многоплодная беременность
Многоплодная беременность Сложение и вычитание дробей с разными знаменателями.
Сложение и вычитание дробей с разными знаменателями. Жілік сүйекті, бұғананы орнықтыру
Жілік сүйекті, бұғананы орнықтыру Абдоминальная хирургия. Кишечный шов
Абдоминальная хирургия. Кишечный шов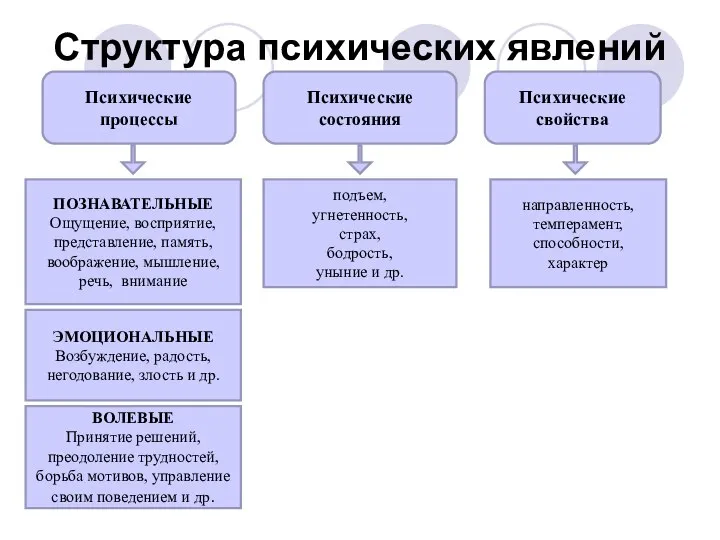 Структура психических явлений
Структура психических явлений Cardiac-Arrest.9103963.powerpoint
Cardiac-Arrest.9103963.powerpoint Психология общения. Техники успешного общения при манипуляции
Психология общения. Техники успешного общения при манипуляции Механизмы, лежащие в основе запуска аутоиммунной патологии
Механизмы, лежащие в основе запуска аутоиммунной патологии Нарушение кровообращения: Патология гемостаза. Тромбоз. Эмболия. Стаз. Шок
Нарушение кровообращения: Патология гемостаза. Тромбоз. Эмболия. Стаз. Шок Психолого-педагогическое развитие детей 6-7 лет
Психолого-педагогическое развитие детей 6-7 лет Особенности метаболизма детей, занимающихся спортом
Особенности метаболизма детей, занимающихся спортом 07.2019 уход за пациентами различного профиля
07.2019 уход за пациентами различного профиля Обструктивная уропатия
Обструктивная уропатия Роль ортопедических мероприятий в комплексном лечении болезней пародонта. Принципы шинирования
Роль ортопедических мероприятий в комплексном лечении болезней пародонта. Принципы шинирования Пищевое поведение
Пищевое поведение Имплантация в стоматологии
Имплантация в стоматологии Болезнь Ходжкина (лимфогранулематоз)
Болезнь Ходжкина (лимфогранулематоз)