Содержание
- 2. 2.1 FICK’S LAW Adolf Fick in 1955 first described the molecular diffusion in an isothermal, isobaric
- 3. Where, JA is the molar flux of component A in the Z direction. CA is the
- 4. 2.2 Diffusion coefficient The proportionality factor of Fick’s law is called diffusivity or diffusion coefficient which
- 5. Diffusivity decreases with increase in pressure (DAB∝1/p for moderate ranges of pressures, up to 25 atm)
- 6. The diffusivity increases with increase in temperature (DAB∝T1.5) because random thermal movement of molecules increases with
- 7. Diffusivity of gas, liquid, and solid The diffusivity is generally higher for gases (in the range
- 8. Diffusion is almost impossible in solids (in the range of 10-13 m2/s) because the particles are
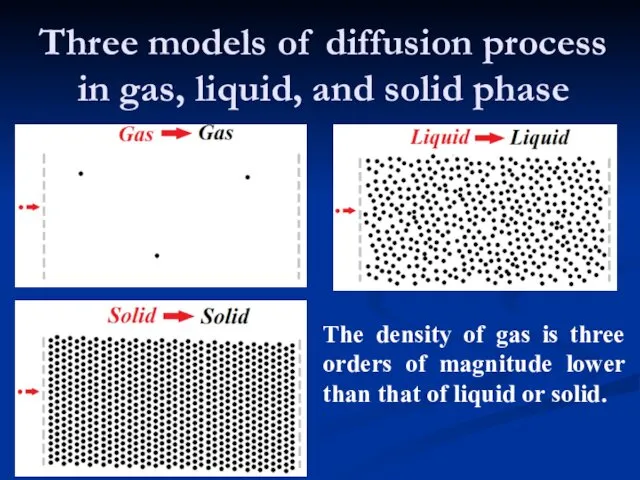
- 9. Three models of diffusion process in gas, liquid, and solid phase The density of gas is
- 10. 2.3 Ratio between heat and molecular diffusivity (Le) The Le number of gas is generally about
- 11. 2.3 Measurement of gas-phase diffusion coefficient (a) Twin-bulb method
- 12. Two bulbs are connected by a narrow tube. In the beginning two bulbs are evacuated and
- 13. where, a is cross sectional area of the connecting tube. If pA1 and pA2 are partial
- 14. Applying the above boundary conditions, the Equation is integrated to obtain the expression of DAB as
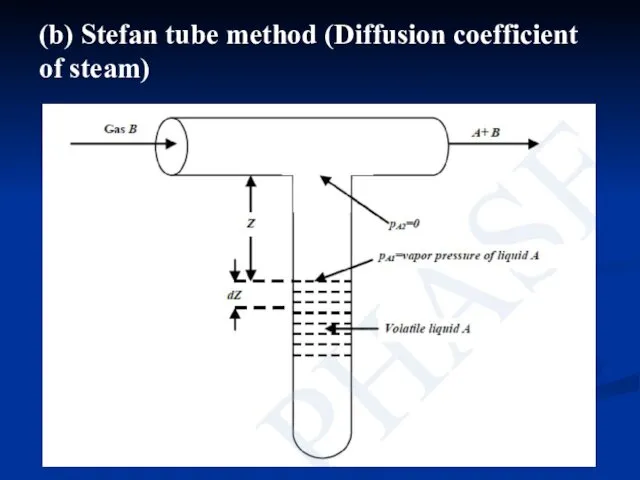
- 15. (b) Stefan tube method (Diffusion coefficient of steam)
- 16. Stefan tube consists of a T-tube, placed in a constant temperature bath. Air pump supply air,
- 17. where, partial pressure of A at liquid surface, pA1 is equal to vapor pressure at the
- 18. 2.4 Estimation of gas diffusion coefficient where, T is temperature in K MA, MB are molecular
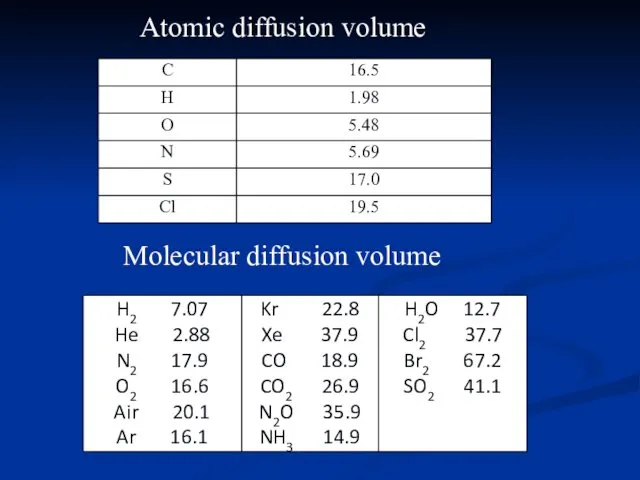
- 19. Atomic diffusion volume Molecular diffusion volume
- 20. Please calculate the molecular diffusion coefficient of n-butanol C4H10O (B) diffusing through air (A) at 298.9K
- 21. Stokes-Einstein Equation Liquid diffusivity varies linearly with absolute temperature and inversely proportional to viscosity of the
- 22. Semi-empirical Equation: Wilke-Chang Equation
- 23. 2.6 Diffusion in porous media Porous materials in nature and industry: sand stone, porous rock, filter
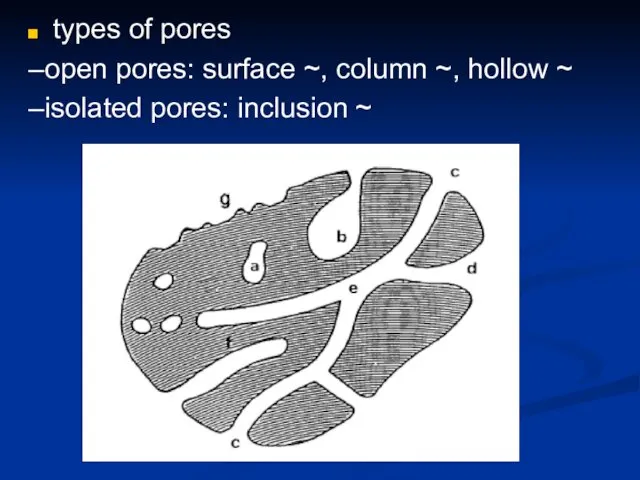
- 24. types of pores –open pores: surface ~, column ~, hollow ~ –isolated pores: inclusion ~
- 25. Pore size: (generally pore width): the distance between two opposite walls of the pore –Micropores (
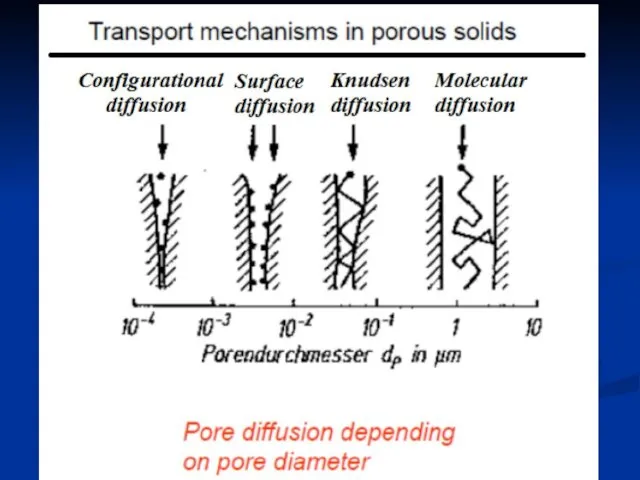
- 26. Diffusion phenomena in porous solids Molecular diffusion Knudsen diffusion Surface diffusion –not of technical importance Configurational
- 28. Molecular diffusion (Collision principle) The probability of collision between molecules and molecules is very high, while
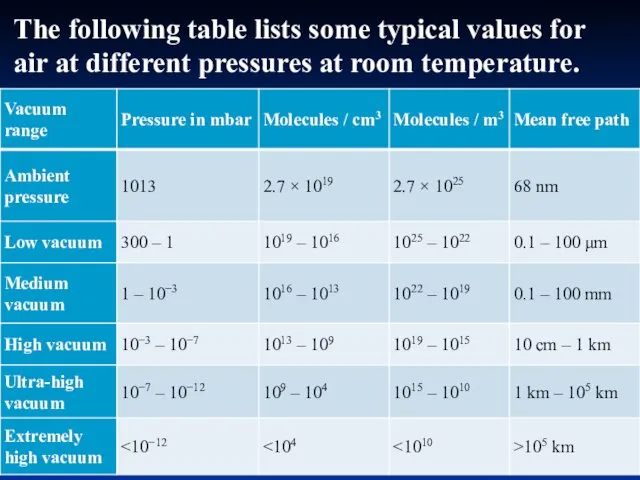
- 29. The following table lists some typical values for air at different pressures at room temperature.
- 30. Knudsen diffusion (Collision principle) Surface diffusion (Adsorption principle) Adsorption balance is established in the walls. The
- 31. Configurational diffusion –pore diameter within molecular dimensions (0.3-1 nm) as for zeolites –diffusion coefficients are smaller
- 33. Скачать презентацию
























 Имунитет дегеніміз не
Имунитет дегеніміз не Механическая желтуха
Механическая желтуха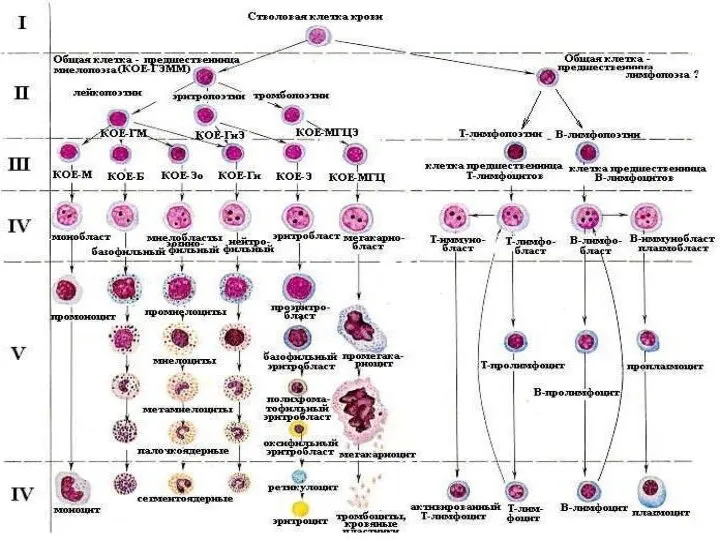 Болезни системы крови
Болезни системы крови Дозирование в фармацевтической технологии
Дозирование в фармацевтической технологии Центр социальной работы и канистерапии Открытые сердца на базе общественного приюта для животных
Центр социальной работы и канистерапии Открытые сердца на базе общественного приюта для животных Дифференциальная диагностика
Дифференциальная диагностика Нейропатии и повреждения периферических нервов у пациентов с травмой опорно-двигательного аппарата
Нейропатии и повреждения периферических нервов у пациентов с травмой опорно-двигательного аппарата Хвороба Аддісона важка форма стадії декомпенсації. Аддісонічна криза
Хвороба Аддісона важка форма стадії декомпенсації. Аддісонічна криза Здоровье лиц пожилого и старческого возраста
Здоровье лиц пожилого и старческого возраста Механическая обработка корневых каналов
Механическая обработка корневых каналов Амбулаторлы хирургиялық қызметті ұйымдастыру
Амбулаторлы хирургиялық қызметті ұйымдастыру Anatomy of lower repiratory system
Anatomy of lower repiratory system БЛХ. Гипоталамо-гипофизарные заболевания
БЛХ. Гипоталамо-гипофизарные заболевания Физиология выделения. Физиология почек и водно-солевого обмена
Физиология выделения. Физиология почек и водно-солевого обмена ՄԻԱՎ-í³ñ³Ï
ՄԻԱՎ-í³ñ³Ï Заманауи технологияларды қолдану арқылы жүрек ырғағының бұзылысын қалпына келтіру
Заманауи технологияларды қолдану арқылы жүрек ырғағының бұзылысын қалпына келтіру Способы оказания первой помощи
Способы оказания первой помощи Тістерді егеуге қолданылатын абразивті материалдар
Тістерді егеуге қолданылатын абразивті материалдар Бинокулярное зрение. Косоглазие
Бинокулярное зрение. Косоглазие Жедел ревматизмдік қызба
Жедел ревматизмдік қызба Система крови
Система крови Жедел аппендицит
Жедел аппендицит Маниакально-депрессивный психоз. Биполярное расстройство. Другие аффективные расстройства
Маниакально-депрессивный психоз. Биполярное расстройство. Другие аффективные расстройства Мезенхимальные дистрофии
Мезенхимальные дистрофии Психическое развитие ребенка в пренатальный период
Психическое развитие ребенка в пренатальный период Психотропные средства
Психотропные средства Thinking About Psychology. The Science of Mind and Behavior 3e
Thinking About Psychology. The Science of Mind and Behavior 3e Особенности сестринского процесса при работе с детьми разного возраста
Особенности сестринского процесса при работе с детьми разного возраста