Содержание
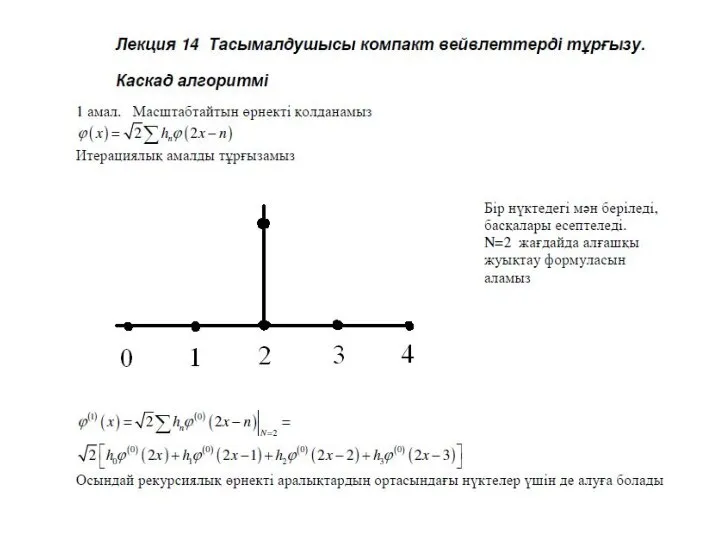
- 2. Лекция 1. Кесіндідегі тригонометриялық жүйе L2 [-π, π] функциялар кеңістігі. Функциялардың ортогоналдығы. Ортогонал функциялар жүйенің толықтығы.
- 3. Лекция 2. Жинақталу түрлері және Фурье қатарының жинақталу шарттары Жинақталуды түрлері: Чезаро бойынша орташа мағынада жинақталу
- 4. f – шектелген 2π периодты, 1-ші текті үзілістері болуы мүмкін фунция болсын. Әр нүктеде f функцияның
- 5. Лекция 3. Кесіндідегі және сандық түзудегі ортонормал жүйелер Ең жиы қолданатын ортонормал жүйелер Тригонометриялық жүйе Лежандра.
- 6. Лекция 4. Сигнал спектрі. Гиббс қүбылысы Периодты функция үшін сигнал спектрі - Фурье қатарының коэффициенттер жиыны.
- 30. Лаплас түрлендіруі. Жеке формулалар
- 31. Лаплас түрлендіруінің кері формуласы
- 33. Колданулары : кеңістікте цилиндр координаттарында Лаплас теңдеуінің шешімдерін алу үшін Лаплас түрлендіруінің қолдануы – дифференциалды теңдеулердің
- 41. Скачать презентацию
![Лекция 1. Кесіндідегі тригонометриялық жүйе L2 [-π, π] функциялар кеңістігі. Функциялардың](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1304426/slide-1.jpg)




































 Презентация Эволюция таможенных процедур в таможенной практике России
Презентация Эволюция таможенных процедур в таможенной практике России Обчислювальна техніка та мікропроцесори
Обчислювальна техніка та мікропроцесори Основные требования к органу по сертификации персонала в соответствии со стандартом ISO/IEC 17024
Основные требования к органу по сертификации персонала в соответствии со стандартом ISO/IEC 17024 Национальная программа развития сети автомобильных дорог в России
Национальная программа развития сети автомобильных дорог в России Федеральное агентство по образованию Российской Федерации Российский государственный университет нефти и газа им. И.М. Губкина
Федеральное агентство по образованию Российской Федерации Российский государственный университет нефти и газа им. И.М. Губкина  Влияние коммуникативных действий учащихся старших классов на формирование навыка командной игры в баскетбол
Влияние коммуникативных действий учащихся старших классов на формирование навыка командной игры в баскетбол Резисторды мультиметрмен тексеру
Резисторды мультиметрмен тексеру Управление различиями
Управление различиями Развитие ораторского искусства в ХХI века Корнев т-114
Развитие ораторского искусства в ХХI века Корнев т-114 Политическая культура, ее сущность и роль
Политическая культура, ее сущность и роль Uniforme scolaire
Uniforme scolaire Ручное изготовление кольца с использование традиционных материалов
Ручное изготовление кольца с использование традиционных материалов Темп роста радужной форели на различных кормах
Темп роста радужной форели на различных кормах Мови програмування
Мови програмування Дымковская игрушка
Дымковская игрушка Окружающий мир 1 класс Тема: «Откуда в наш дом приходит электричество»
Окружающий мир 1 класс Тема: «Откуда в наш дом приходит электричество» Saint Petersburg Sightseeings
Saint Petersburg Sightseeings Метрические задачи
Метрические задачи  Презентация "Обзор нефтегазовой отрасли Казахстана" - скачать презентации по Экономике
Презентация "Обзор нефтегазовой отрасли Казахстана" - скачать презентации по Экономике Алгоритмы обработки массивов
Алгоритмы обработки массивов  СВОЙСТВА МИОКАРДА. АВТОМАТИЯ СЕРДЦА
СВОЙСТВА МИОКАРДА. АВТОМАТИЯ СЕРДЦА «Божественная» пропорция
«Божественная» пропорция Федеральный закон "О техническом регулировании"
Федеральный закон "О техническом регулировании" Ресурсы проекта. Производственные ресурсы организации. Lean-менеджмент (бережливое производство)
Ресурсы проекта. Производственные ресурсы организации. Lean-менеджмент (бережливое производство) decision-making under risk прийняття рішень в умовах ризику
decision-making under risk прийняття рішень в умовах ризику МСБО 24 Розкриття інформації щодо зв'язаних сторін
МСБО 24 Розкриття інформації щодо зв'язаних сторін  Числа и векторы
Числа и векторы ВКР «Влияние занятий гимнастикой пилатес на развитие физических качеств, гибкости и силы у подростков 12-14 лет»
ВКР «Влияние занятий гимнастикой пилатес на развитие физических качеств, гибкости и силы у подростков 12-14 лет»