Содержание
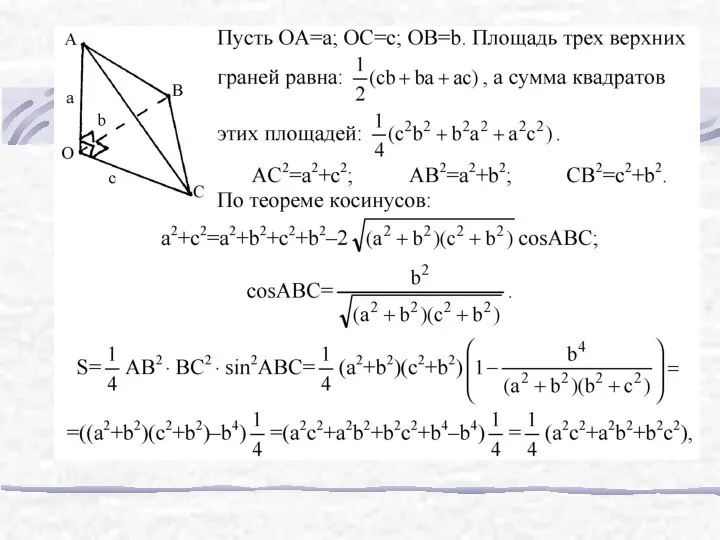
- 2. Все плоские углы тетраэдра ОABC при вершине О — прямые. Докажите, что квадрат площади треугольника ABC
- 4. Три формулировки теоремы Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов; Квадрат
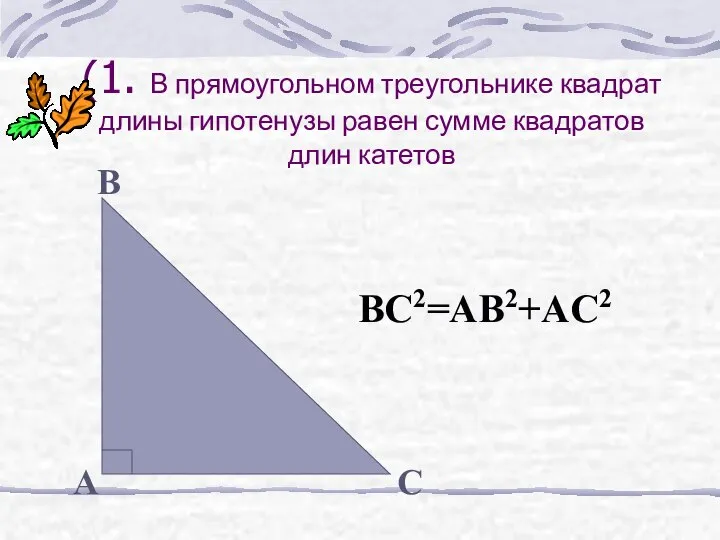
- 5. С A B BC2=AB2+AC2 (1. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов
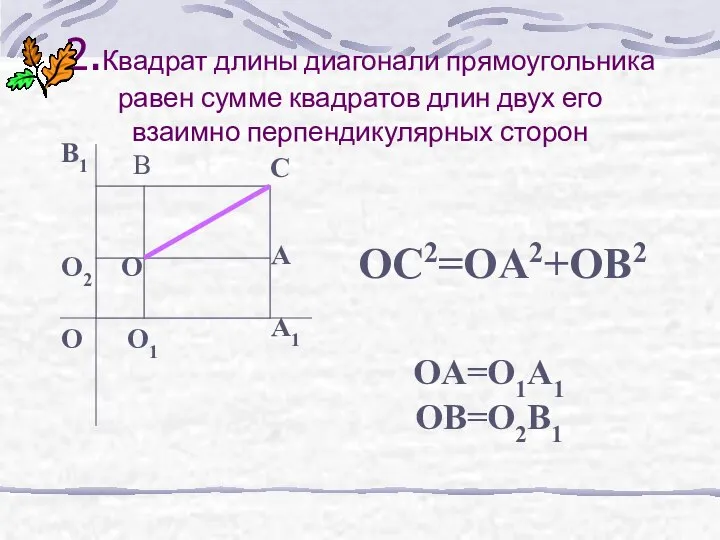
- 6. 2.Квадрат длины диагонали прямоугольника равен сумме квадратов длин двух его взаимно перпендикулярных сторон O O1 O
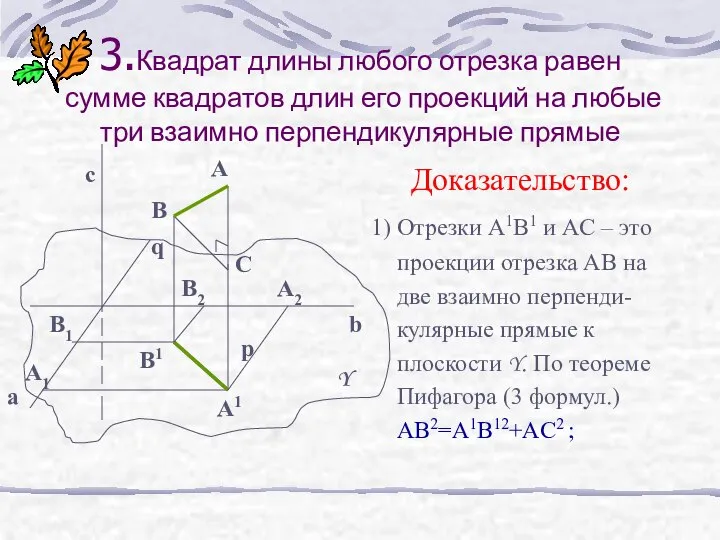
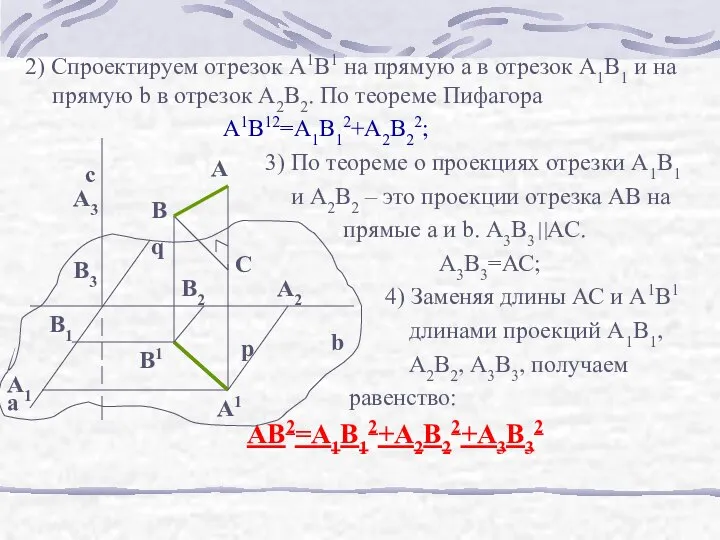
- 7. 3.Квадрат длины любого отрезка равен сумме квадратов длин его проекций на любые три взаимно перпендикулярные прямые
- 8. 2) Спроектируем отрезок A1B1 на прямую а в отрезок А1В1 и на прямую b в отрезок
- 10. Скачать презентацию


 Решение задач на тему: «Пирамида. Площадь пирамиды» Литвинов О.А. ГБОУ СОШ № 873
Решение задач на тему: «Пирамида. Площадь пирамиды» Литвинов О.А. ГБОУ СОШ № 873  Прямая и обратная теорема Подготовила Ученица 7 «Б» класса Булатова Мария Учитель: Мизей Н. И.
Прямая и обратная теорема Подготовила Ученица 7 «Б» класса Булатова Мария Учитель: Мизей Н. И. Геометрия 7 класс. Начальные геометрические сведения. Решение задач.
Геометрия 7 класс. Начальные геометрические сведения. Решение задач. Сумма двух векторов. Геометрия 9 класс
Сумма двух векторов. Геометрия 9 класс Презентация по геометрии Теорема о трех перпендикулярах
Презентация по геометрии Теорема о трех перпендикулярах  Тригонометрические формулы Обобщающий урок Автор – составитель: Певцова О.В. учитель математики высшей квалификацион
Тригонометрические формулы Обобщающий урок Автор – составитель: Певцова О.В. учитель математики высшей квалификацион Тема урока Тетраэдр и его сечения
Тема урока Тетраэдр и его сечения  Презентация Многоугольники
Презентация Многоугольники Треугольники вокруг нас - презентация по Геометрии
Треугольники вокруг нас - презентация по Геометрии Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве  Эти знакомые и незнакомые многогранники Проект выполнили учащиеся 10А класса Иванов И., Бубнов Н., Татохин П., Кувшинова К., Ферюльс
Эти знакомые и незнакомые многогранники Проект выполнили учащиеся 10А класса Иванов И., Бубнов Н., Татохин П., Кувшинова К., Ферюльс Тетраэдр
Тетраэдр Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника  Стереометрия «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят,
Стереометрия «Только неотступно следуя законам геометрии, архитекторы древности могли создать свои шедевры. Не случайно говорят, Обобщение и систематизация сведений о треугольниках - презентация по Геометрии
Обобщение и систематизация сведений о треугольниках - презентация по Геометрии Площадь
Площадь Тема урока:ПРОЕЦИРОВАНИЕ Что называется проекцией предмета на плоскость? Что такое проецирование? Какие существуют виды про
Тема урока:ПРОЕЦИРОВАНИЕ Что называется проекцией предмета на плоскость? Что такое проецирование? Какие существуют виды про Тема урока: Построение сечений параллелепипеда
Тема урока: Построение сечений параллелепипеда  Я думаю, Дон, что в моей голове это просто не может уместиться. Я просто не знаю, как мне удастся все это выучить. Я думаю, Дон, что в м
Я думаю, Дон, что в моей голове это просто не может уместиться. Я просто не знаю, как мне удастся все это выучить. Я думаю, Дон, что в м Выполнил: Студент гр 916 Ковардинов Павел
Выполнил: Студент гр 916 Ковардинов Павел  Лозовой Андрей
Лозовой Андрей Египетский треугольник - презентация по Геометрии_
Египетский треугольник - презентация по Геометрии_ Золотое сечение - презентация по Геометрии
Золотое сечение - презентация по Геометрии Исследовательская работа по геометрии на тему: «Геометрические построения на плоскости».
Исследовательская работа по геометрии на тему: «Геометрические построения на плоскости». Признаки равенства треугольников Урок в 7 классе Г Учитель Мошнина Ирина Владимировна
Признаки равенства треугольников Урок в 7 классе Г Учитель Мошнина Ирина Владимировна Сфера и шар. МОУ СОШ №256 г.Фокино.
Сфера и шар. МОУ СОШ №256 г.Фокино.  Правильные фигуры и тела Выполнила: Беленкова Ольга Александровна
Правильные фигуры и тела Выполнила: Беленкова Ольга Александровна СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР Учитель: Попова Т.А. ГБОУ СОШ №684
СЕЧЕНИЯ ПРОСТРАНСТВЕННЫХ ФИГУР Учитель: Попова Т.А. ГБОУ СОШ №684