Численное решение систем линейных алгебраических уравнений СЛАУ

Общий вид СЛАУ

где a – коэффициенты системы,
b – свободные

Запись СЛАУ в матричной форме

При решении СЛАУ возможно возникновение 3 случаев:

1. Пример:
2. Пример:
3. Пример:

2 класса методов решения СЛАУ:

1. Прямые методы.
2. Итерационные методы.

Прямые методы

Достоинство: устойчивость методов.
Недостаток: точность решения зависит от особенностей метода и

Итерационные методы

Достоинство: точность решения задается пользователем.
Недостаток: методы являются неустойчивыми.

Метод Гаусса (метод последовательного исключения неизвестных)
Является прямым методом.
Исходные данные:
А
В

Алгоритм метода Гаусса:

Ввод исходных данных.
Прямой ход.
Обратный ход.
Вывод результатов.

Метод Гаусса для 3 уравнений с 3-мя неизвестными (система 3-го порядка)
1.

Получим следующее:
3. Новые обозначения:

Новая система:
4. х2:
5. х2 подставляется во все оставшиеся уравнения системы.

Получим следующее:
6. Новые обозначения:
Новая система в верхнетреугольном виде:

7. Неизвестные вычисляются в обратном порядке (обратный ход):

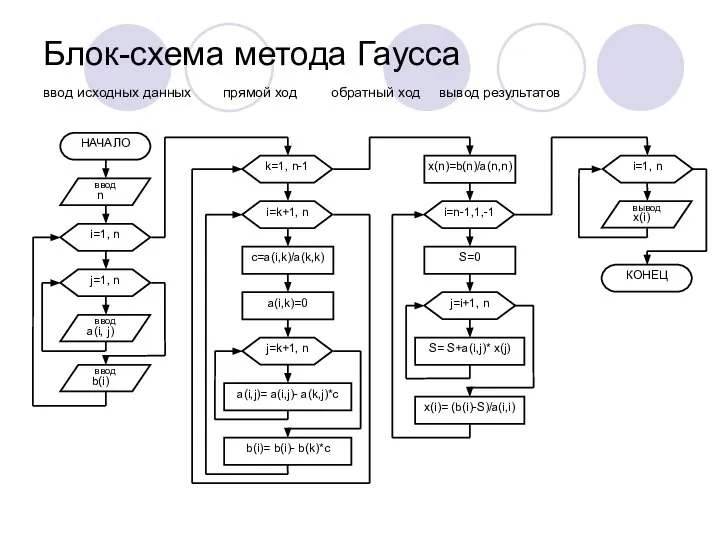
Блок-схема метода Гаусса ввод исходных данных прямой ход обратный ход вывод результатов

ЗАМЕЧАНИЕ
В случае единственности решения СЛАУ методом Гаусса всегда находится необходимое решение.
Необходимо

Метод Зейделя (метод простых итераций)

Является итерационным методом.
Исходные данные:
А
В
Х(0)
Е

Метод Зейделя для 3 уравнений с 3-мя неизвестными
Из 1-го уравнения выражаем

Получим новую систему:
2. В правую часть 1-го уравнения подставляем начальные приближения

ЗАМЕЧАНИЕ
Метод Зейделя является итерационным, итерации сходятся не всегда.
Итерации всегда сходятся при

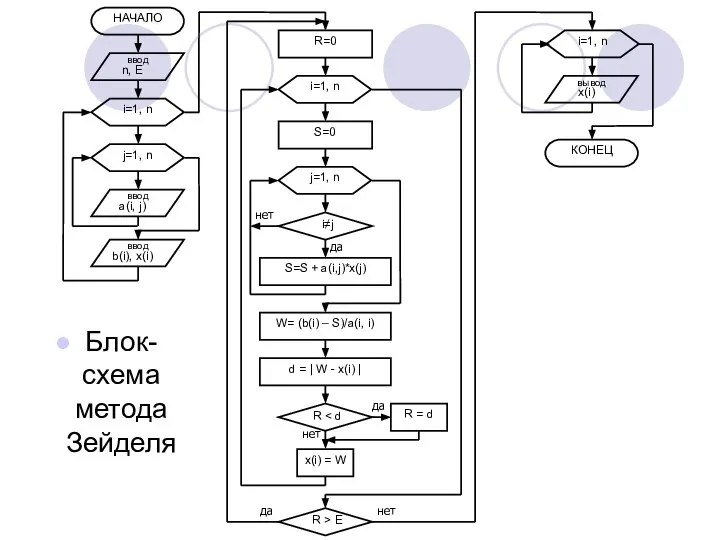
Блок-схема метода Зейделя

Метод Крамера для решения СЛАУ 2-го и 3-го порядка
Прямой метод. Метод

Условие существования единственного решения СЛАУ
det A ≠ 0

Метод Крамера для системы 2-го порядка

Метод Крамера для системы 3-го порядка

Окончательные формулы:

Для систем более высоких порядков метод Крамера практически не применяется

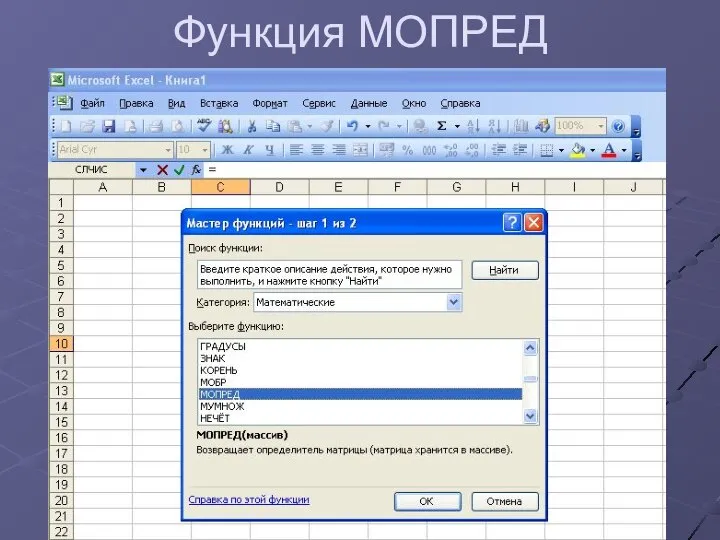
Реализация метода Крамера в электронных таблицах
Microsoft Excell
Функция
МОПРЕД(матрица)

Функция МОПРЕД