Содержание
- 2. Теорема 4.1 Если дифференцируема в точке то в точке условия Коши-Римана. Доказательство.
- 3. ■
- 4. Пусть f(z)∈C(g), Теорема 4.2 Если в точке дифференцируемая в точке то Доказательство. и
- 5. Обозначим
- 6. ■ Замечания.
- 7. 2. Теорема 4.2 не обратная к теореме 4.1 Если f(z) дифференцируема в точке z0, то она
- 8. Основное определение. f(z) дифференцируемая в ∀ z∈g, f ’(z) ∈C(g) называется аналитической функцией в g. Обозначение:
- 9. Доказательство. Необходимость. Из Т.4.1 => Достаточность. Из Т.4.2 т.к. Т.к. ■
- 10. Замечание. Далее будет показано, что из Основное замечание. Условие —лишнее. Альтернативное определение. f(z) дифференцируемая в ∀
- 11. Теорема 4.4 Если и в точке дифференцируемая в точке то Теорема 4.5 Необходимым и достаточным условиями
- 12. Оказывается, что производная «аналитической» функции непрерывна в g, причем для ∀n f(n)(z)∈C(g), т.е. класс «аналитических» функций
- 13. Следствия условий Коши-Римана Обратно, пара гармонических в g функций u(x,y) и v(x,y), связанные условиями Коши- Римана,
- 15. Свойства аналитических функций.
- 17. ■
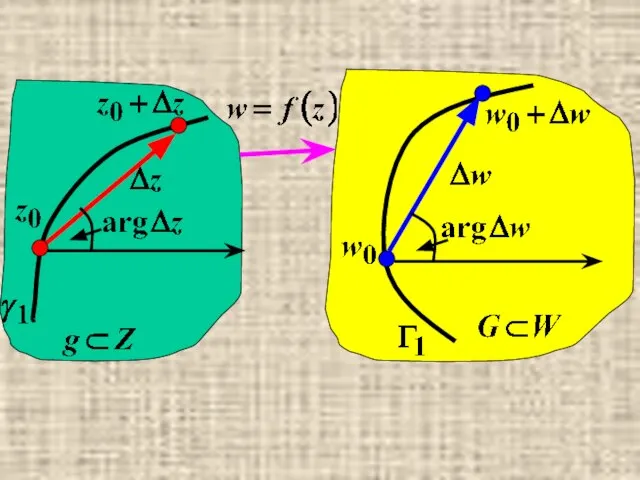
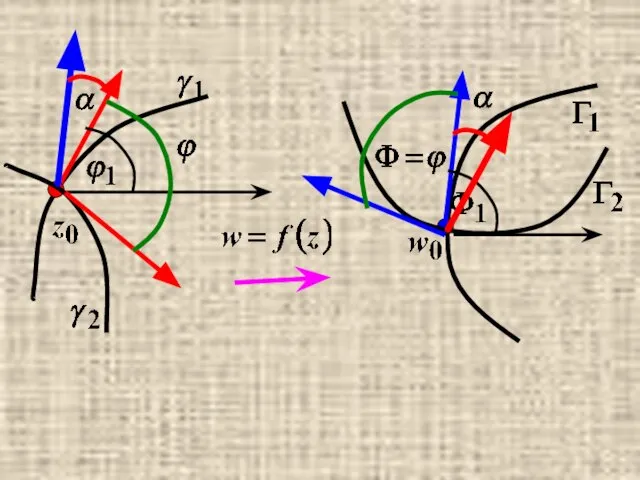
- 21. Геометрический смысл модуля и аргумента производной аналитической функции.
- 24. Свойство постоянства растяжения.
- 25. определяет величину угла, на который нужно повернуть касательную к ∀ гладкой кривой γ, проходящей через точку
- 26. Свойство сохранения углов. для ∀γ2 : z0∈γ2 : Φ2=ϕ2+α => Φ=Φ2-Φ1=ϕ2-ϕ1=ϕ (сохраняется величина и направление углов).
- 28. Скачать презентацию

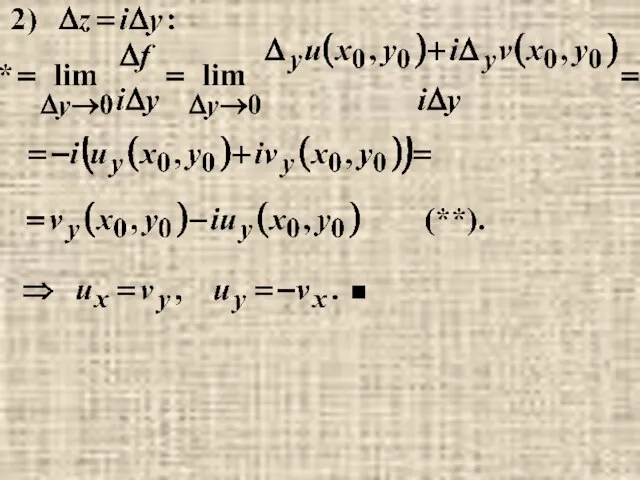

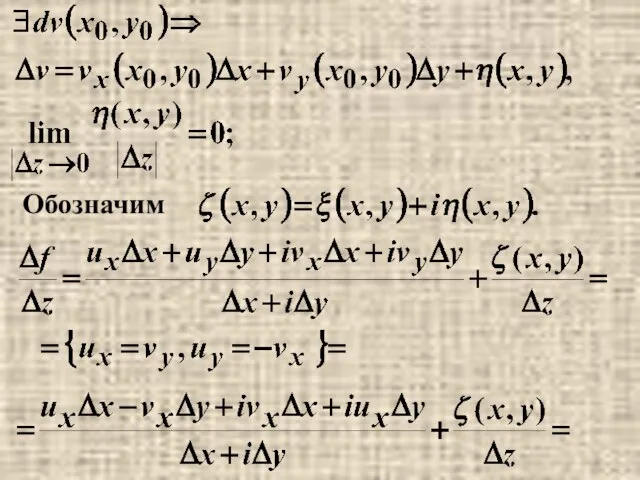
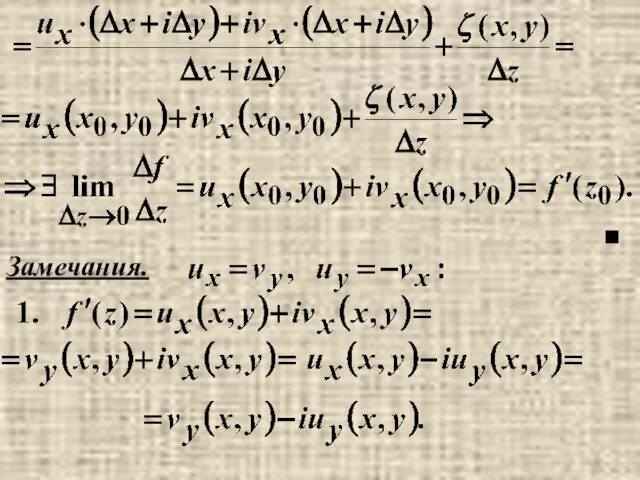







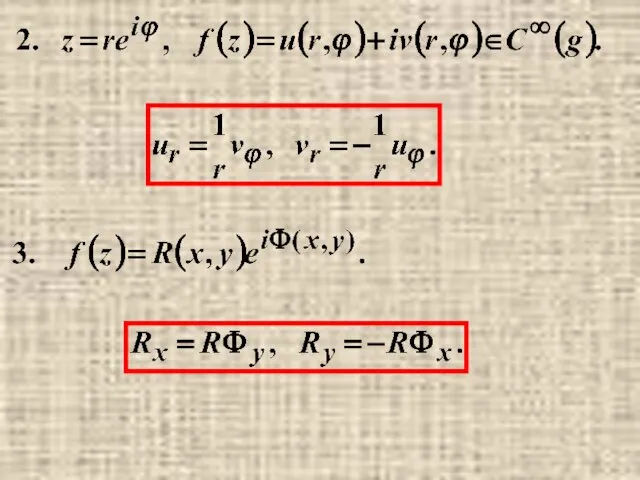
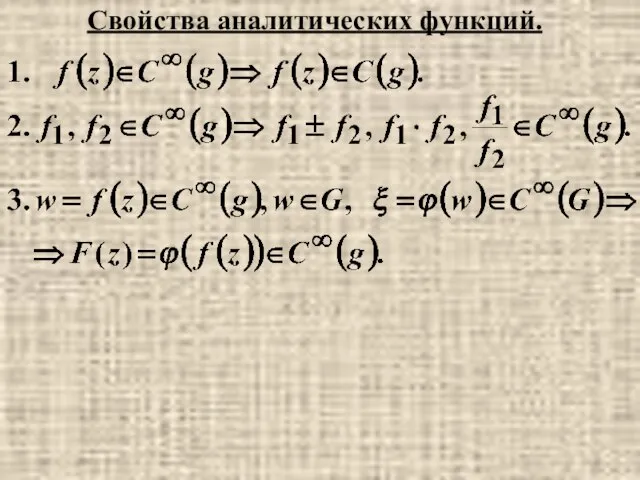
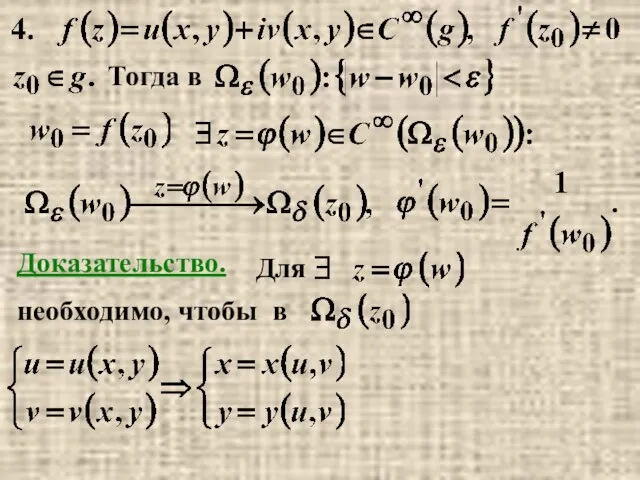



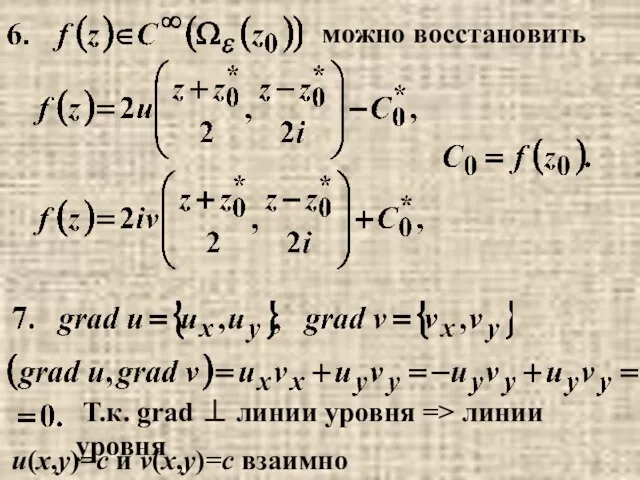




 Измерение высоты здания основываясь на правилах подобия треугольников
Измерение высоты здания основываясь на правилах подобия треугольников Три подхода к построению множества целых неотрицательных чисел. Часть 1
Три подхода к построению множества целых неотрицательных чисел. Часть 1 Сечение и секущая плоскость
Сечение и секущая плоскость Математические головоломки
Математические головоломки Теоретическая разминка. Десятичные дроби
Теоретическая разминка. Десятичные дроби Последний герой. Игра
Последний герой. Игра Искусственные нейронные сети. (Лекция 1)
Искусственные нейронные сети. (Лекция 1) Минутка занимательной математики
Минутка занимательной математики Урок математики 4 класс Учитель: Дубская Г.А.
Урок математики 4 класс Учитель: Дубская Г.А. Обобщающий урок по теме: «Уравнения»
Обобщающий урок по теме: «Уравнения» Решение неравенств
Решение неравенств Исследовательская работа по математике на тему: Математическая статистика в действии
Исследовательская работа по математике на тему: Математическая статистика в действии Угол между прямыми. Задания для устного счета. Упражнение 4
Угол между прямыми. Задания для устного счета. Упражнение 4 Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 7
Компьютерный практикум по алгебре в среде Matlab. Практическое занятие 7 ДРУЖОК правила по математике для начальных классов
ДРУЖОК правила по математике для начальных классов Собирательные числительные
Собирательные числительные Статистическое изучение взаимосвязи показателей таможенной статистики
Статистическое изучение взаимосвязи показателей таможенной статистики Функция y=sin x, ее свойства и график
Функция y=sin x, ее свойства и график Основы расчета надежности технических систем
Основы расчета надежности технических систем Презентация для класса Проверяем, верно ли» 1 класс
Презентация для класса Проверяем, верно ли» 1 класс  Погрешности измерений
Погрешности измерений Законы сложения и вычитания 5 класс
Законы сложения и вычитания 5 класс Площадь сечения в прямоугольном параллелепипеде. Задачи
Площадь сечения в прямоугольном параллелепипеде. Задачи Презентация по математике "Кабінет" - скачать
Презентация по математике "Кабінет" - скачать  Презентация на тему Измерение отрезков
Презентация на тему Измерение отрезков  Проект по математике «Таинственные числа 7 и 12»
Проект по математике «Таинственные числа 7 и 12» Деление дробей. 8 класс
Деление дробей. 8 класс Числовые выражения, содержащие знаки + и -
Числовые выражения, содержащие знаки + и -