Визначення. Декартовим добутком множин X і Y називається множина X*Y всіх
впорядкованих пар (x, у) таких, що x X, у Y.
Визначення. Відношенням між множинами X і Y (або відношенням з X в Y) називається будь-яка підмножина R декартового добутку X*Y. Якщо множини X і Y збігаються, то відношення між множинами X і Y називають бінарним відношенням на множині X.
Приклад. Нехай X = {а, b, с, d}, Y = {1, 2, 3, 4, 5}. Тоді множина комбінацій R={(а, 1), (b, 2), (с, 3), (d, 4)} є відношенням з X в Y.
Зазвичай відношення задаються не шляхом задання підмножини R декартового добутку X*Y, а шляхом задання властивості пар (x, у), що належать цій підмножині R.
Приклад. Відношення R = {(4, 4), (3, 3), (2, 2), (4, 2)} на множині X = {4, 3, 2} можна визначити як властивість "Ділиться" на цій підмножині цілих чисел.
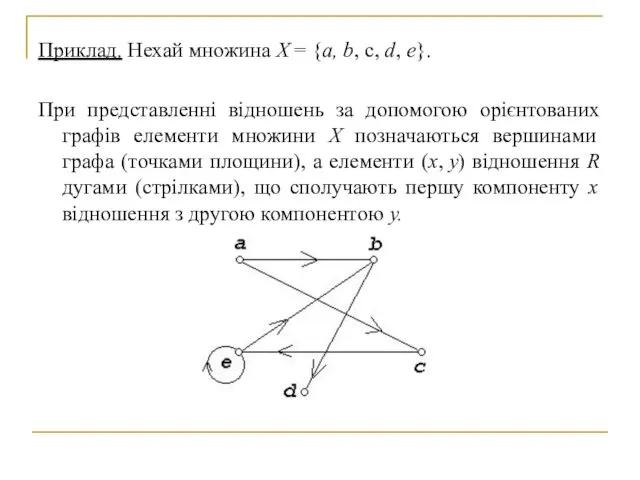
2.1. Поняття бінарного відношення







 Аттестационная работа. Рабочая программа работы объединения по интересам Школа Пифагора. (5 класс)
Аттестационная работа. Рабочая программа работы объединения по интересам Школа Пифагора. (5 класс) Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла
Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин
Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин Мир треугольников
Мир треугольников Способы решения квадратных уравнений
Способы решения квадратных уравнений Квадрат теңдеу және оның түбірлері
Квадрат теңдеу және оның түбірлері Анализ геометрических тел
Анализ геометрических тел Аттестационная работа. Методическая разработка по выполнению проекта «В мире задач»
Аттестационная работа. Методическая разработка по выполнению проекта «В мире задач» Учимся писать цифры
Учимся писать цифры 2 класс МБОУ « СОШ № 2 г. Рузы»
2 класс МБОУ « СОШ № 2 г. Рузы»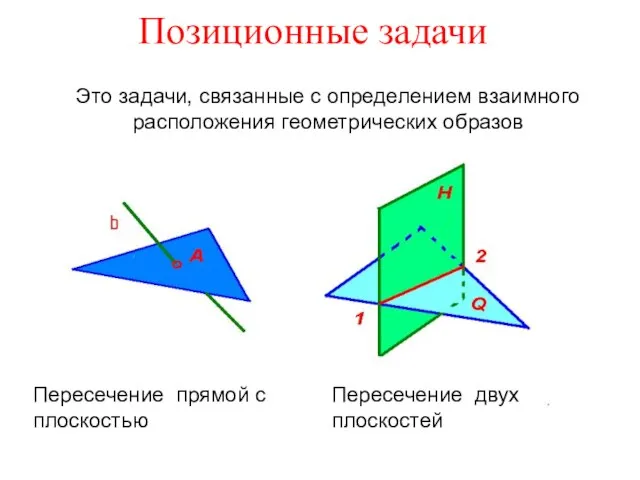 Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей
Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей ЕГЭ по математике: задания В10 и В13
ЕГЭ по математике: задания В10 и В13 Квадратичная функция
Квадратичная функция История математики. Алгебра и геометрия
История математики. Алгебра и геометрия Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями Задачи практического характера в разных областях науки и техники
Задачи практического характера в разных областях науки и техники Свойства логарифмов
Свойства логарифмов Презентация на тему Открытие десятичных дробей
Презентация на тему Открытие десятичных дробей  Талица умножения - это просто
Талица умножения - это просто Математика и я. Язык математики – язык многих наук
Математика и я. Язык математики – язык многих наук Знакомство с цилиндром
Знакомство с цилиндром Бенефис линейной функции
Бенефис линейной функции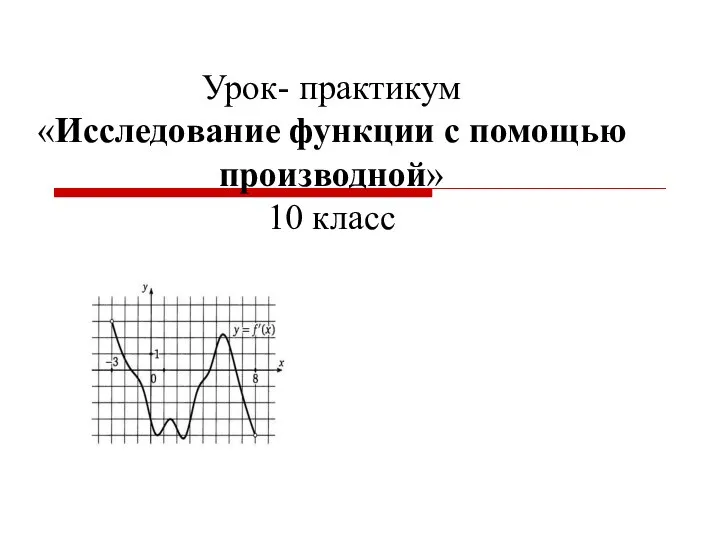 Урок- практикум «Исследование функции с помощью производной» 10 класс
Урок- практикум «Исследование функции с помощью производной» 10 класс Подготовка к ЕГЭ
Подготовка к ЕГЭ Задачи. Задание 8
Задачи. Задание 8 Функция y=sinx
Функция y=sinx Геометрическое место точек
Геометрическое место точек