Функция y = (x)

Актуальность – собрать сведения по теме в связи с подготовкой к

Определение модуля

В математике через |x| обозначается абсолютная величина, или модуль числа

1.D(f)=(-∞;+∞)
2.E(f)=[0;+∞)
3.Ограничена снизу
4.Возрастает на[0;+∞)
убывает на(-∞;0]
5.Чётная функция
6.
7.Непрерывна

х

у

Свойства функции

График функции

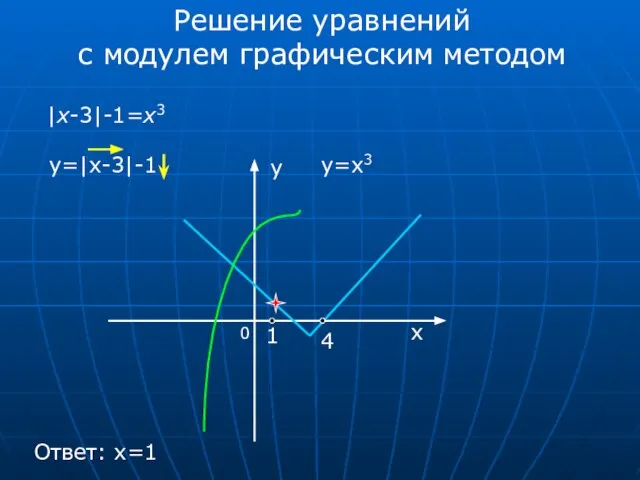
Решение уравнений
с модулем графическим методом

|x-3|-1=x3

y=|x-3|-1

y=x3

0

x

1

4

Ответ: x=1

у

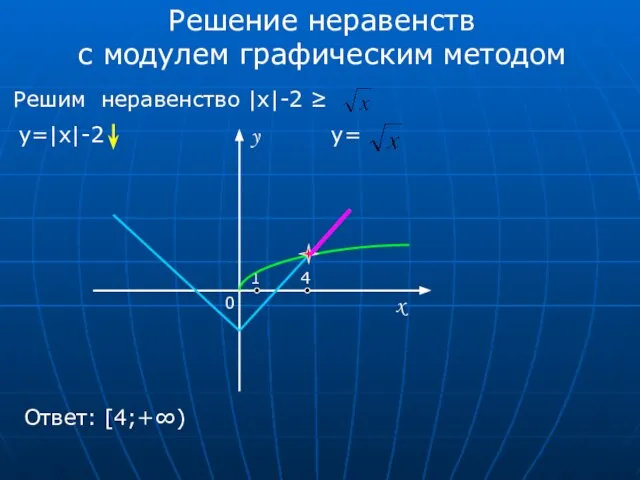
Решение неравенств
с модулем графическим методом

Решим неравенство |x|-2 ≥

y=|x|-2

y=

0

x

y

1

4

Ответ: [4;+∞)

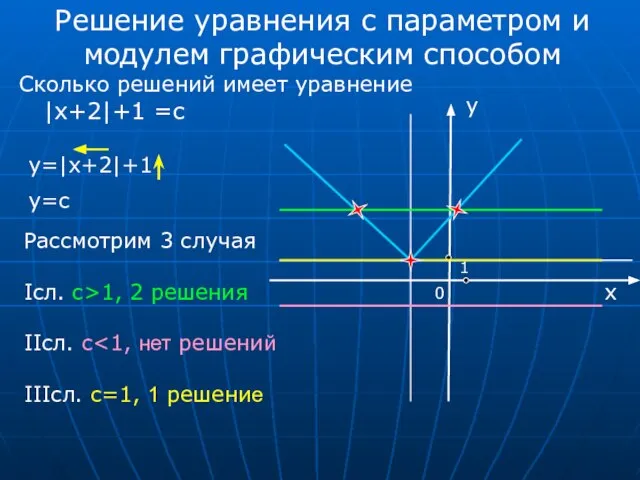
0

x

1

Решение уравнения с параметром и
модулем графическим способом

Рассмотрим 3 случая
Iсл. c>1,

Аналитический метод решения уравнения с модулем

Решим уравнение|x-3|=5
I способ

Рассмотрим два случая

1

Показательные уравнения с модулем

2|x+2| = 16
2|x+2| = 24
|x+2| = 4
I случай II

Логарифмическое уравнение с модулем

log2(|x-2| - 1) = 1
|x-2| - 1 =

Алгоритм решения уравнений с модулем

Найти нули модулей.
Отметить нули на координатной прямой.
Решить

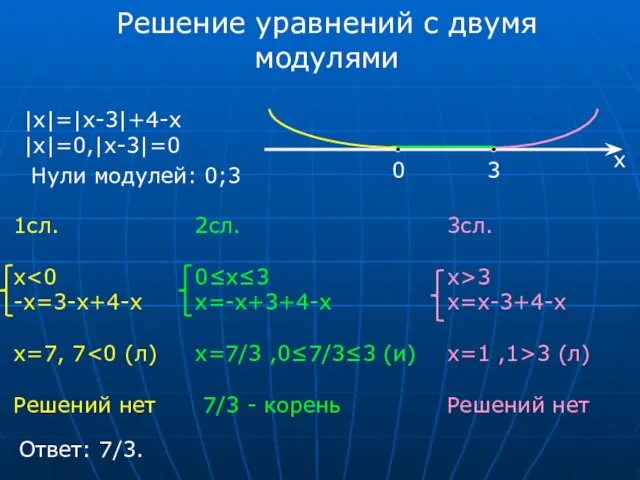
Решение уравнений с двумя модулями

|x|=|x-3|+4-x
|x|=0,|x-3|=0

Нули модулей: 0;3

0

3

х

1сл.
x<0
-x=3-x+4-x
x=7, 7<0 (л)
Решений нет

2сл.
0≤x≤3
x=-x+3+4-x
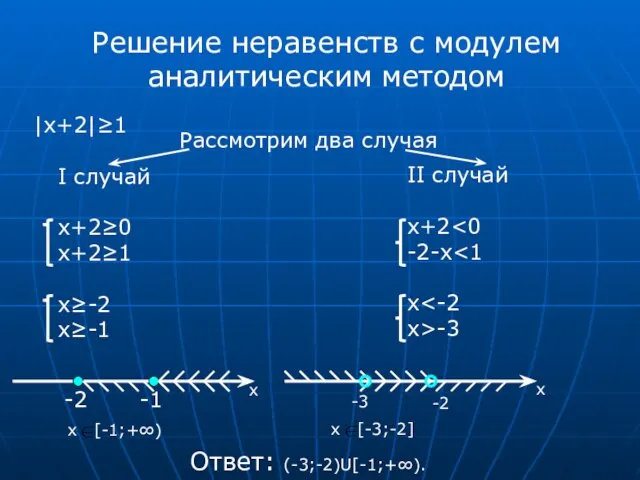
x=7/3

Решение неравенств с модулем аналитическим методом

|x+2|≥1

Рассмотрим два случая

I случай
x+2≥0
x+2≥1
x≥-2
x≥-1

II случай

Решение неравенств с модулем различными методами

Третий способ. Имеем: |x-2.5|>2.
Геометрически выражение |x-2.5|

Алгоритм решения неравенств с модулем

Найти нули модулей.
Отметить нули на координатной прямой.
Решить

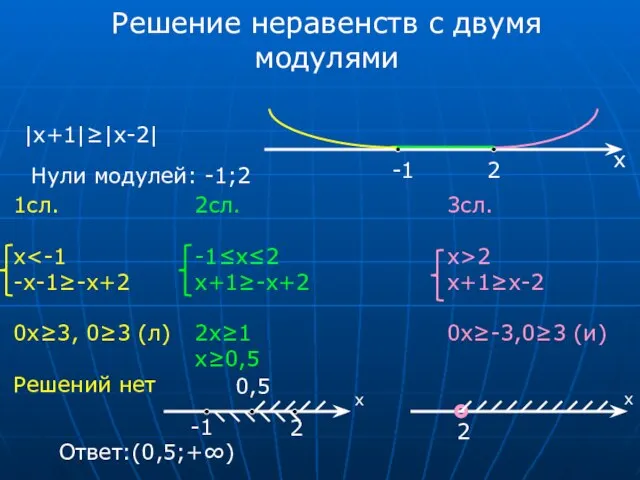
Решение неравенств с двумя модулями

|x+1|≥|x-2|

Нули модулей: -1;2

-1

2

х

1сл.
x<-1
-x-1≥-х+2
0x≥3, 0≥3 (л)
Решений нет

2сл.
-1≤x≤2
х+1≥-x+2
2х≥1
х≥0,5

3сл.

Тригонометрические уравнения с модулем

|sin(x+ )|=1
I случай II случай
sin(x+ )=1

Тригонометрические уравнения с модулем

|cosx|=cos(x+ )

I cлучай
cosx<0
-cosx=cos(x+ )
cos( +x)=cos(x+ )
x+ =x+

Тригонометрические уравнения с модулем

|cosx|=cos(x+ )

II cлучай
cosx≥0
cosx=cos(x+ )
cos(x)=cos(x+ )
x =x+ +2

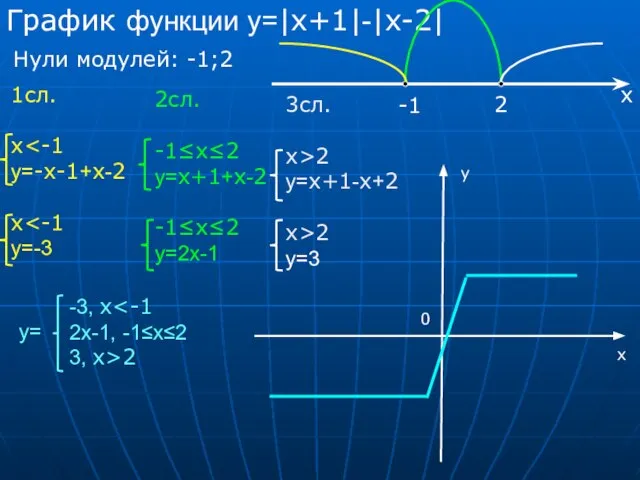
График функции у=|x+1|-|x-2|

Нули модулей: -1;2

1сл.
x<-1
у=-x-1+х-2
x<-1
у=-3

2сл.
-1≤x≤2
у=х+1+x-2
-1≤x≤2
у=2х-1

3сл.
x>2
у=х+1-х+2
x>2
у=3

-3, x<-1
2х-1, -1≤x≤2
3, x>2

х

у

0

у=

Считают, что термин предложил использовать Котс, ученик Ньютона. Знак модуля введен

Выводы

В ходе работы над проектом моя гипотеза не подтвердилась.
Я не только