Содержание
- 2. Квадратные уравнения (методы решения)
- 3. Азбука квадратного уравнения
- 4. Неполные квадратные уравнения:
- 5. D Корней нет D = 0 D > 0
- 6. b = 2k (четное число)
- 7. Теорема Виета x1 и х2 – корни уравнения x1 и х2 – корни уравнения
- 8. Решите уравнения 5x2 = 15x 3x2 - 75 = 0 x2- 7x + 12 = 0
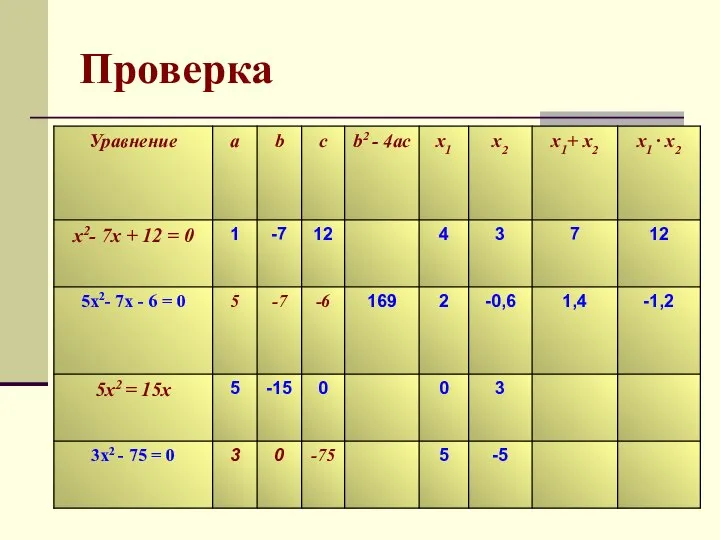
- 9. Проверка
- 10. Специальные методы: Метод выделения квадрата двучлена. Метод «переброски» старшего коэффициента На основании теорем: Далее
- 11. Цель: привести квадратное уравнение общего вида к неполному квадратному уравнению. Пример: Метод выделения квадрата двучлена.
- 12. Корни квадратных уравнений и связаны соотношениями и В некоторых случаях бывает удобно решать сначала не данное
- 13. На основании теорем: Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй
- 14. Общие методы: Разложение на множители; Введение новой переменной; Графический метод. Далее
- 15. Метод разложения на множители привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х)
- 16. Введение новой переменной. Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой
- 17. Решение уравнений с отрицательными дискриминантами i2 = — 1. Решите уравнение x2 + 2х + 5
- 18. В Древней Индии были распространены публичные соревнования в решении трудных задач. Задачи часто облекались в стихотворную
- 20. Скачать презентацию




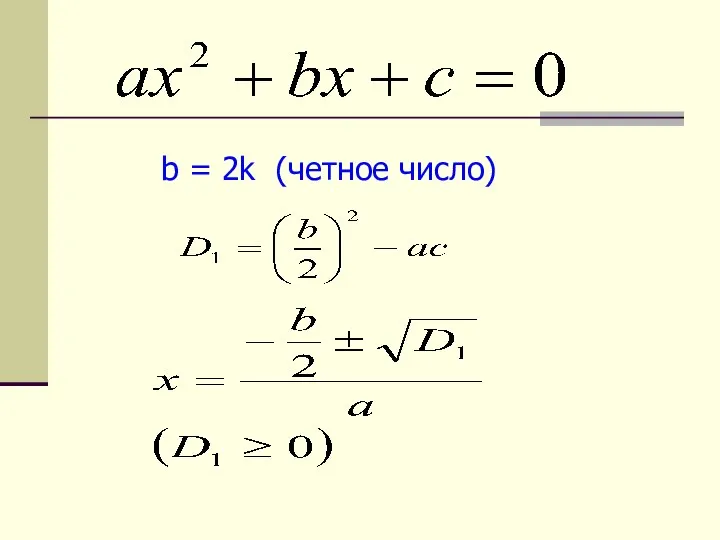











 Аттестационная работа. Рабочая программа работы объединения по интересам Школа Пифагора. (5 класс)
Аттестационная работа. Рабочая программа работы объединения по интересам Школа Пифагора. (5 класс) Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла
Муниципальное бюджетное образовательное учреждение «Лопхаринская средняя общеобразовательная школа» Урок математики в 5 кла Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин
Обработка экспериментальных данных. Счетная обработка полученных данных. Расчет относительных величин Мир треугольников
Мир треугольников Способы решения квадратных уравнений
Способы решения квадратных уравнений Квадрат теңдеу және оның түбірлері
Квадрат теңдеу және оның түбірлері Анализ геометрических тел
Анализ геометрических тел Аттестационная работа. Методическая разработка по выполнению проекта «В мире задач»
Аттестационная работа. Методическая разработка по выполнению проекта «В мире задач» Учимся писать цифры
Учимся писать цифры 2 класс МБОУ « СОШ № 2 г. Рузы»
2 класс МБОУ « СОШ № 2 г. Рузы»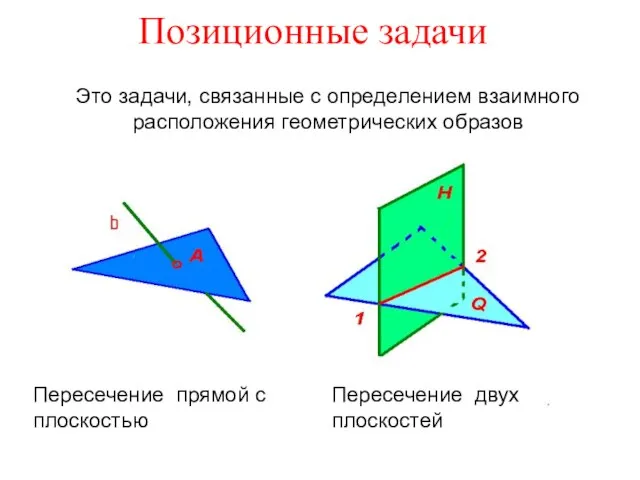 Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей
Позиционные задачи. Пересечение прямой с плоскостью. Пересечение двух плоскостей ЕГЭ по математике: задания В10 и В13
ЕГЭ по математике: задания В10 и В13 Квадратичная функция
Квадратичная функция История математики. Алгебра и геометрия
История математики. Алгебра и геометрия Числовые и буквенные выражения. (5 класс)
Числовые и буквенные выражения. (5 класс) Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями Задачи практического характера в разных областях науки и техники
Задачи практического характера в разных областях науки и техники Свойства логарифмов
Свойства логарифмов Презентация на тему Открытие десятичных дробей
Презентация на тему Открытие десятичных дробей  Талица умножения - это просто
Талица умножения - это просто Математика и я. Язык математики – язык многих наук
Математика и я. Язык математики – язык многих наук Знакомство с цилиндром
Знакомство с цилиндром Бенефис линейной функции
Бенефис линейной функции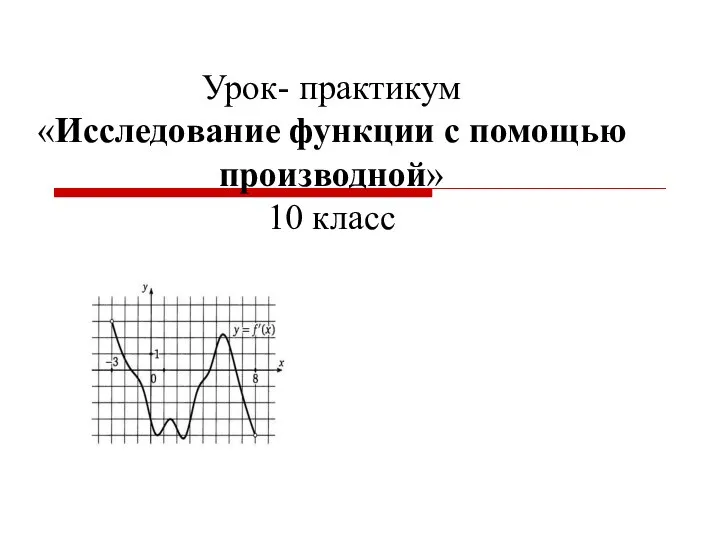 Урок- практикум «Исследование функции с помощью производной» 10 класс
Урок- практикум «Исследование функции с помощью производной» 10 класс Подготовка к ЕГЭ
Подготовка к ЕГЭ Задачи. Задание 8
Задачи. Задание 8 Функция y=sinx
Функция y=sinx Геометрическое место точек
Геометрическое место точек