Лекция 08. Однородные координаты

Содержание

Слайд 2

1. Вводные замечания

1. Вводные замечания

Слайд 3

В аналитической геометрии под «координатами» геометрического объекта понимается любая совокупность чисел, позволяющая однозначно определить этот объект.

В аналитической геометрии под «координатами» геометрического объекта понимается любая совокупность чисел, позволяющая однозначно определить этот объект.

Слайд 4

Примеры 1) Точка определяется своими прямоугольными координатами x, y или своими полярными координатами r, ϕ.

Примеры
1) Точка определяется своими прямоугольными координатами x, y или своими полярными

координатами r, ϕ.
Слайд 5

Примеры 1) Точка определяется своими прямоугольными координатами x, y или своими

Примеры
1) Точка определяется своими прямоугольными координатами x, y или своими полярными

координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
Слайд 6

Примеры 1) Точка определяется своими прямоугольными координатами x, y или своими

Примеры
1) Точка определяется своими прямоугольными координатами x, y или своими полярными

координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0.
Слайд 7

Примеры 1) Точка определяется своими прямоугольными координатами x, y или своими

Примеры
1) Точка определяется своими прямоугольными координатами x, y или своими полярными

координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
Слайд 8

Примеры 1) Точка определяется своими прямоугольными координатами x, y или своими

Примеры
1) Точка определяется своими прямоугольными координатами x, y или своими полярными

координатами r, ϕ.
2) Треугольник определяется координатами трех вершин (шесть координат).
3) Прямая линия в плоскости x, y – это геометрическое место всех точек P(x, y), координаты которых удовлетворяют уравнению ax + by + c = 0. Поэтому три числа a, b, c можно назвать «координатами» этой прямой.
4) Конические сечения: окружность, эллипс...
Слайд 9

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x,

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x, y),
троек

чисел (x, y, z) и т.д.
Слайд 10

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x,

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x, y),
троек

чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Слайд 11

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x,

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x, y),
троек

чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
Слайд 12

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x,

То есть, отталкиваемся от множества чисел x, всевозможных пар чисел (x, y),
троек

чисел (x, y, z) и т.д.
Каждый такой элемент (число, пару, тройку...) называем точкой и можем, при необходимости, наглядно интерпретировать.
Приходим к тому, что в физике называют фазовым пространством.
То есть, мы можем уходить из чисто геометрического пространства.
Слайд 13

2. Однородные координаты

2. Однородные координаты

Слайд 14

Обыкновенная аналитическая геометрия: прямоугольные координаты точки на плоскости – это снабжённые

Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на плоскости – это снабжённые

знаками расстояния точки от двух взаимно перпендикулярных осей.
Слайд 15

Обыкновенная аналитическая геометрия: прямоугольные координаты точки на плоскости – это снабжённые

Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на плоскости – это снабжённые

знаками расстояния точки от двух взаимно перпендикулярных осей.
В такой системе координат нет места для несобственных точек проективной плоскости.
Слайд 16

Обыкновенная аналитическая геометрия: прямоугольные координаты точки на плоскости – это снабжённые

Обыкновенная аналитическая геометрия:
прямоугольные координаты точки
на плоскости – это снабжённые

знаками расстояния точки от двух взаимно перпендикулярных осей.
В такой системе координат нет места для несобственных точек проективной плоскости.
Поэтому для использования аналитических методов в проективной геометрии необходимо найти координатную систему, которая включает несобственные точки наравне с обыкновенными.
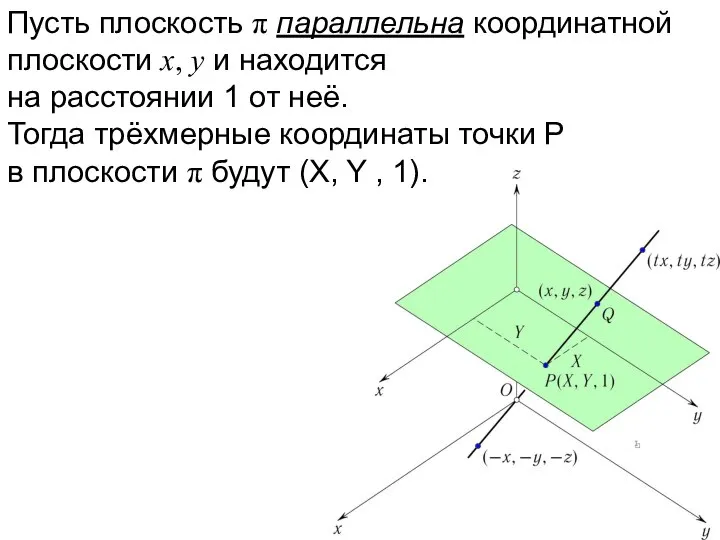
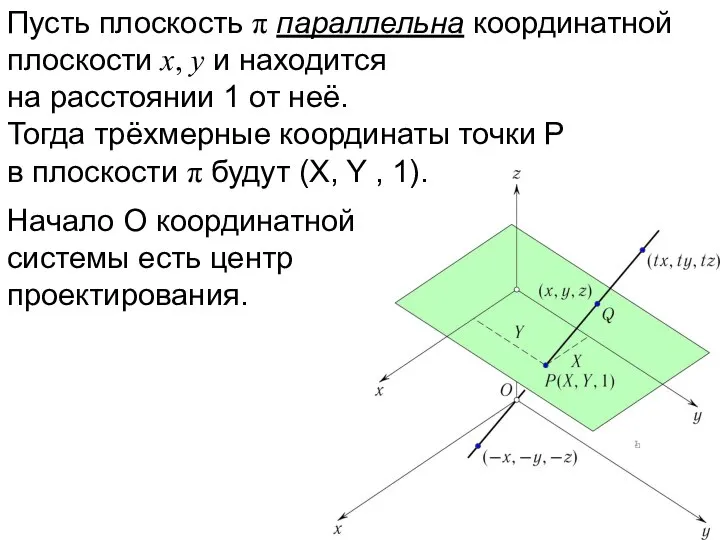
Слайд 17

Пусть плоскость π параллельна координатной плоскости x, y и находится на

Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии

1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Слайд 18

Пусть плоскость π параллельна координатной плоскости x, y и находится на

Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии

1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Слайд 19

Пусть плоскость π параллельна координатной плоскости x, y и находится на

Пусть плоскость π параллельна координатной плоскости x, y и находится
на расстоянии

1 от неё.
Тогда трёхмерные координаты точки P в плоскости π будут (X, Y , 1).
Начало O координатной системы есть центр проектирования.
Тогда всякой точке P взаимно однозначно соответствует прямая OP, проходящая через
начало координат.
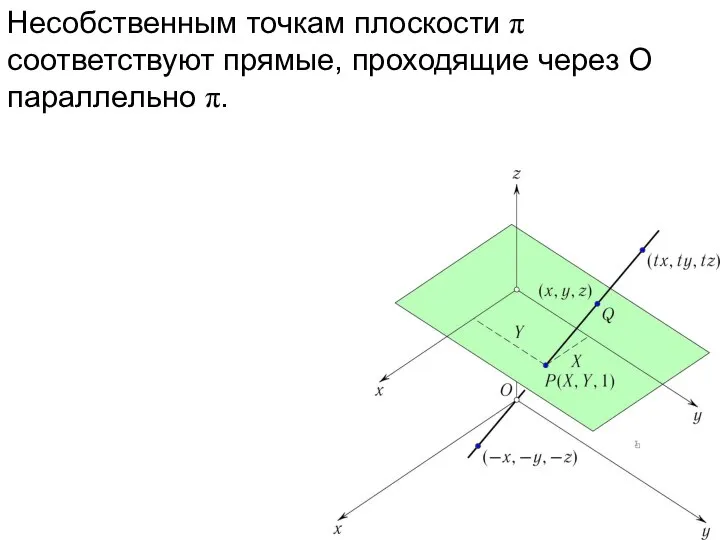
Слайд 20

Несобственным точкам плоскости π соответствуют прямые, проходящие через O параллельно π.

Несобственным точкам плоскости π соответствуют прямые, проходящие через O параллельно π.

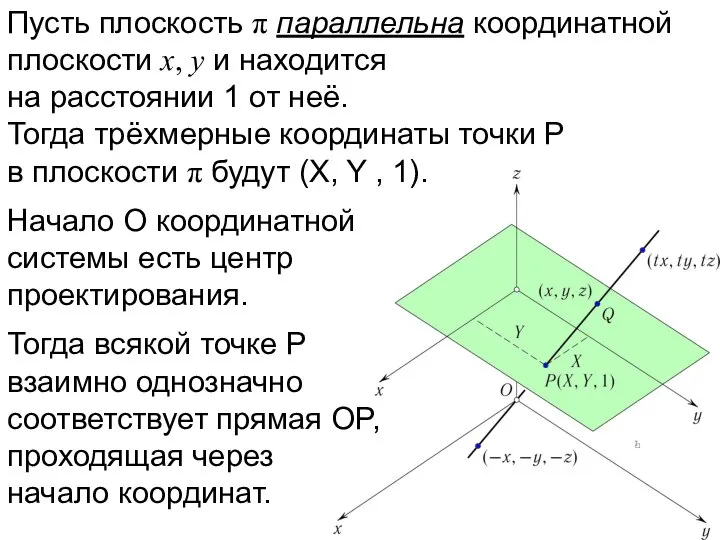
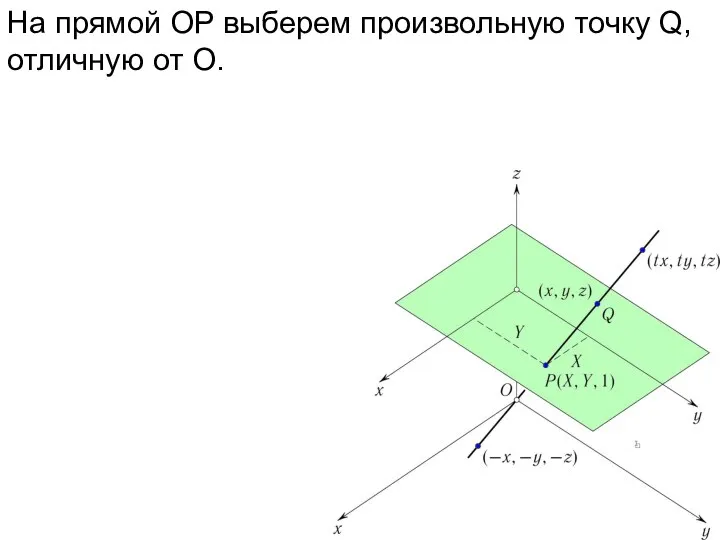
Слайд 21

На прямой OP выберем произвольную точку Q, отличную от O.

На прямой OP выберем произвольную точку Q, отличную от O.

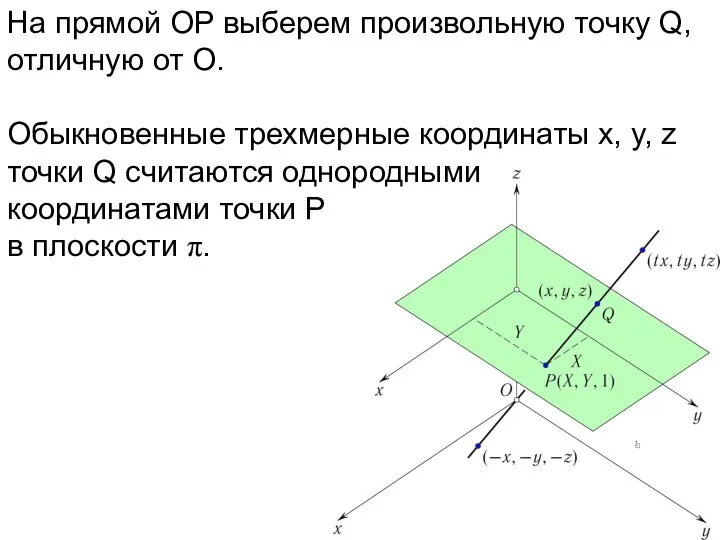
Слайд 22

На прямой OP выберем произвольную точку Q, отличную от O. Обыкновенные

На прямой OP выберем произвольную точку Q, отличную от O.
Обыкновенные трехмерные

координаты x, y, z точки Q считаются однородными
координатами точки P в плоскости π.
Слайд 23

На прямой OP выберем произвольную точку Q, отличную от O. Обыкновенные

На прямой OP выберем произвольную точку Q, отличную от O.
Обыкновенные трехмерные

координаты x, y, z точки Q считаются однородными
координатами точки P в плоскости π.
Координаты (X, Y , 1) самой точки P также являются её однородными координатами.
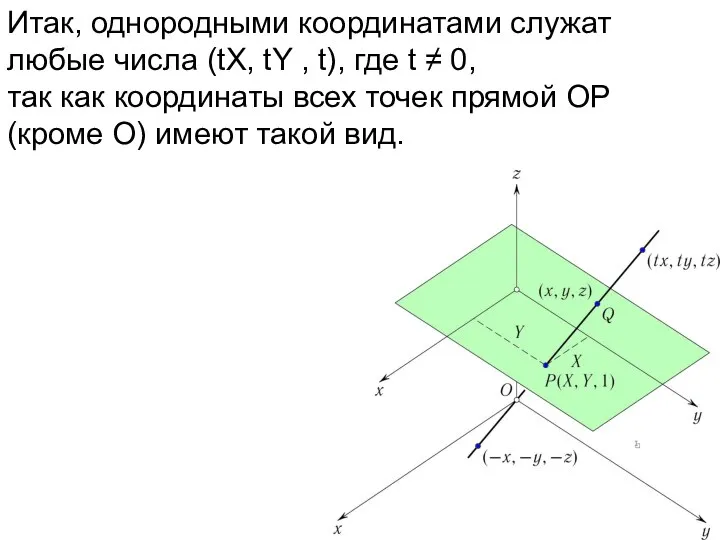
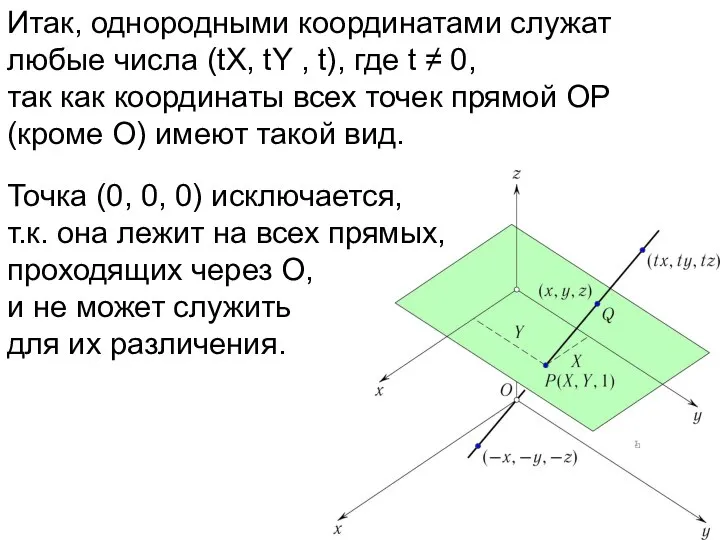
Слайд 24

Итак, однородными координатами служат любые числа (tX, tY , t), где

Итак, однородными координатами служат любые числа (tX, tY , t), где

t ≠ 0,
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
Слайд 25

Итак, однородными координатами служат любые числа (tX, tY , t), где

Итак, однородными координатами служат любые числа (tX, tY , t), где

t ≠ 0,
так как координаты всех точек прямой OP (кроме O) имеют такой вид.
Точка (0, 0, 0) исключается, т.к. она лежит на всех прямых, проходящих через O, и не может служить для их различения.
Слайд 26

В системе однородных координат нужны три числа вместо двух для определения точки.

В системе однородных координат нужны три числа вместо двух для определения

точки.
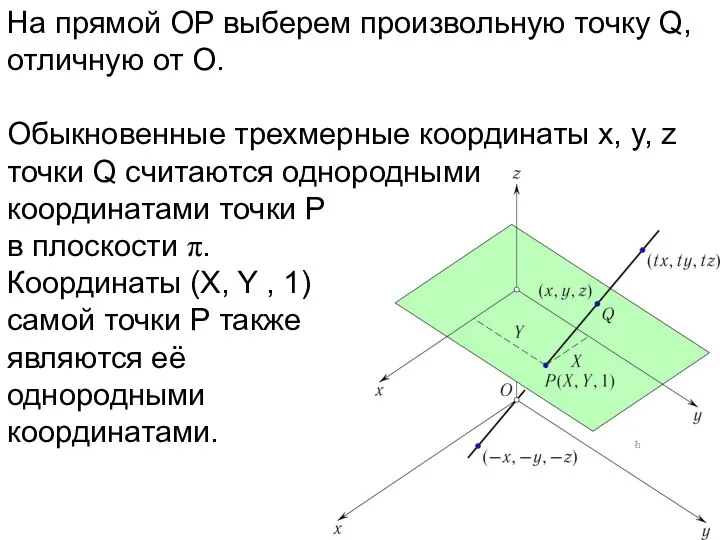
Слайд 27

В системе однородных координат нужны три числа вместо двух для определения

В системе однородных координат нужны три числа вместо двух для определения

точки.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Слайд 28

В системе однородных координат нужны три числа вместо двух для определения

В системе однородных координат нужны три числа вместо двух для определения

точки.
Координаты точки определяются не однозначно, а с точностью до постоянного множителя.
Но эта система охватывает обыкновенные и несобственные точки плоскости π.
Слайд 29

Несобственной точке P соответствует прямая, проходящая через O параллельно π. Любая

Несобственной точке P соответствует прямая, проходящая через O параллельно π.
Любая точка Q на

этой прямой имеет координаты вида (x, y, 0).
Это значит, что однородные координаты несобственных точек плоскости π имеют вид (x, y, 0).
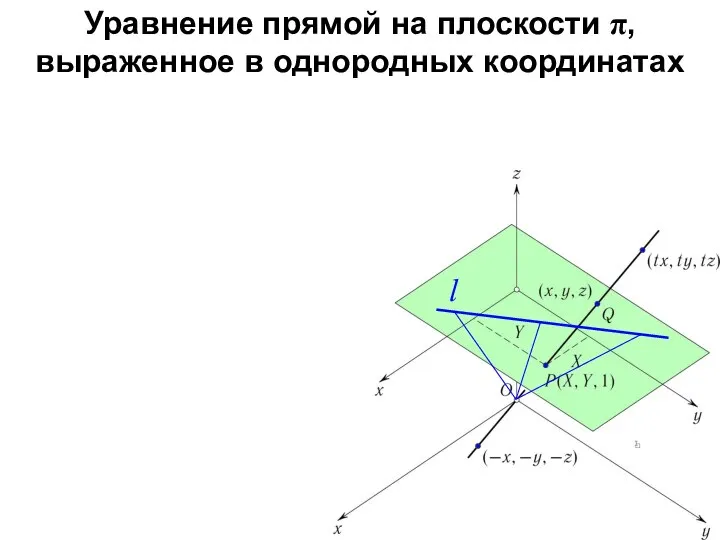
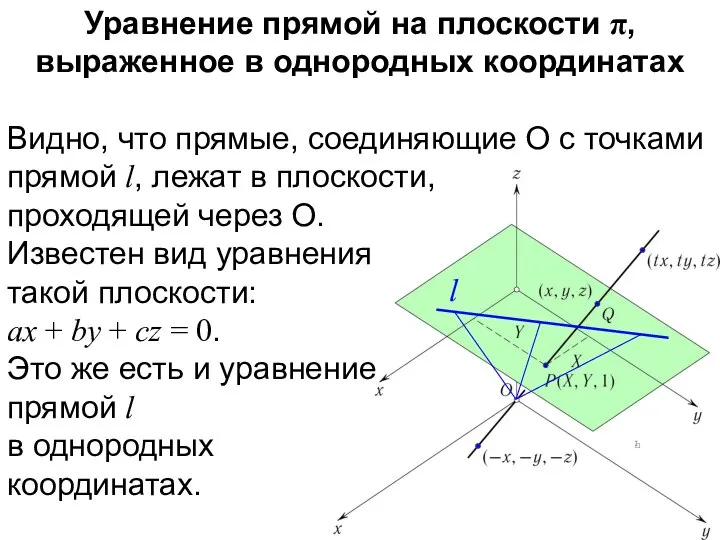
Слайд 30

Уравнение прямой на плоскости π, выраженное в однородных координатах l

Уравнение прямой на плоскости π, выраженное в однородных координатах

l

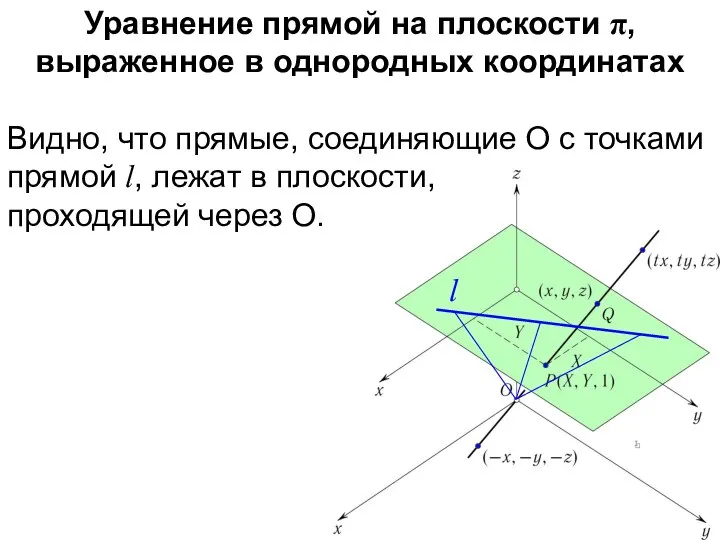
Слайд 31

Уравнение прямой на плоскости π, выраженное в однородных координатах Видно, что

Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,

соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.

l

Слайд 32

Уравнение прямой на плоскости π, выраженное в однородных координатах Видно, что

Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,

соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.

l

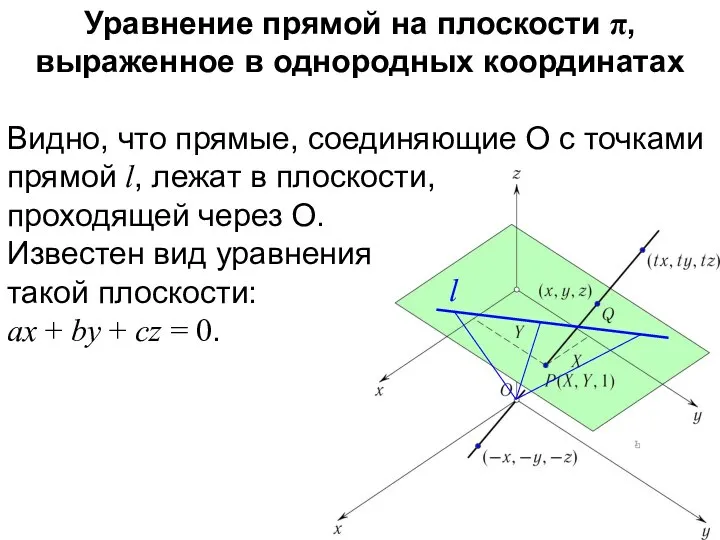
Слайд 33

Уравнение прямой на плоскости π, выраженное в однородных координатах Видно, что

Уравнение прямой на плоскости π, выраженное в однородных координатах
Видно, что прямые,

соединяющие O с точками прямой l, лежат в плоскости,
проходящей через O.
Известен вид уравнения такой плоскости:
ax + by + cz = 0.
Это же есть и уравнение прямой l в однородных координатах.

l

Слайд 34

Рассмотрим чисто аналитическое определение проективной плоскости.

Рассмотрим чисто аналитическое определение проективной плоскости.

Слайд 35

Рассмотрим чисто аналитическое определение проективной плоскости. 1) Точка есть тройка действительных

Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных

чисел (x, y, z), из которых не все равны нулю.
Слайд 36

Рассмотрим чисто аналитическое определение проективной плоскости. 1) Точка есть тройка действительных

Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных

чисел (x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Слайд 37

Рассмотрим чисто аналитическое определение проективной плоскости. 1) Точка есть тройка действительных

Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных

чисел (x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
Слайд 38

Рассмотрим чисто аналитическое определение проективной плоскости. 1) Точка есть тройка действительных

Рассмотрим чисто аналитическое определение проективной плоскости.
1) Точка есть тройка действительных

чисел (x, y, z), из которых не все равны нулю.
2) Две такие тройки (x1, y1, z1) и (x2, y2, z2)
определяют одну и ту же точку, если существует такое t ≠ 0, что
x2 = tx1, y2 = ty1, z2 = tz1.
Потому эти координаты называются однородными.
3) Точка (x, y, z) обыкновенная, если z ≠ 0, и несобственная, если z = 0.
Слайд 39

Прямая линия в плоскости π состоит из всех точек (x, y,

Прямая линия в плоскости π состоит из всех точек (x, y, z),

удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Слайд 40

Прямая линия в плоскости π состоит из всех точек (x, y,

Прямая линия в плоскости π состоит из всех точек (x, y, z),

удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
Слайд 41

Прямая линия в плоскости π состоит из всех точек (x, y,

Прямая линия в плоскости π состоит из всех точек (x, y, z),

удовлетворяющих уравнению вида
ax + by + cz = 0,
где a, b, c – постоянные числа, не все равные нулю.
Несобственные точки плоскости π удовлетворяют уравнению z = 0.
Это уравнение несобственной прямой.
Слайд 42

При произвольном t ≠ 0 тройка чисел (ta, tb, tc) есть

При произвольном t ≠ 0 тройка чисел (ta, tb, tc) есть

координаты той же прямой, поскольку уравнение
(ta)x + (tb)y + (tc)z = 0
удовлетворяется теми же координатными тройками (x, y, z), что и уравнение
ax + by + cz = 0.
Слайд 43

Эти определения полностью симметричны между точкой и прямой: они обе определяются

Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой

чисел – однородными координатами (u, v, w).
Слайд 44

Эти определения полностью симметричны между точкой и прямой: они обе определяются

Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой

чисел – однородными координатами (u, v, w).
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Слайд 45

Эти определения полностью симметричны между точкой и прямой: они обе определяются

Эти определения полностью симметричны между точкой и прямой:
они обе определяются тройкой

чисел – однородными координатами (u, v, w).
Условие того, что точка (x, y, z) лежит на прямой (a, b, c), выражается равенством
ax + by + cz = 0.
Это же есть условие того, что точка с координатами (a, b, c) лежит на прямой с координатами (x, y, z).
Слайд 46

Например, тождество 2 · 3 + 1 · 4 + (−5)

Например, тождество
2 · 3 + 1 · 4 + (−5) ·

2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Слайд 47

Например, тождество 2 · 3 + 1 · 4 + (−5)

Например, тождество
2 · 3 + 1 · 4 + (−5) ·

2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии:
Слайд 48

Например, тождество 2 · 3 + 1 · 4 + (−5)

Например, тождество
2 · 3 + 1 · 4 + (−5) ·

2 = 0
означает, что точка (3, 4, 2) лежит на прямой (2, 1, −5), и что точка (2, 1, −5) лежит на прямой (3, 4, 2).
Эта симметрия есть основа двойственности «точка ↔ прямая» в проективной геометрии: всякое соотношение между точками и прямыми становится некоторым соотношением между прямыми и точками, если координаты точек считать координатами прямых, а координаты прямых – координатами точек.
Слайд 49

Замечание: В евклидовой плоскости X, Y о двойственности не может быть

Замечание:
В евклидовой плоскости X, Y о двойственности не может быть речи,

т.к. уравнение прямой в обыкновенных
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
Слайд 50

Замечание: В евклидовой плоскости X, Y о двойственности не может быть

Замечание:
В евклидовой плоскости X, Y о двойственности не может быть речи,

т.к. уравнение прямой в обыкновенных
координатах
aX + bY + c = 0
несимметрично относительно X, Y и a, b, c.
Только включение в рассмотрение
бесконечно удаленных элементов
(точек и прямой)
обеспечивает применимость
принципа двойственности.
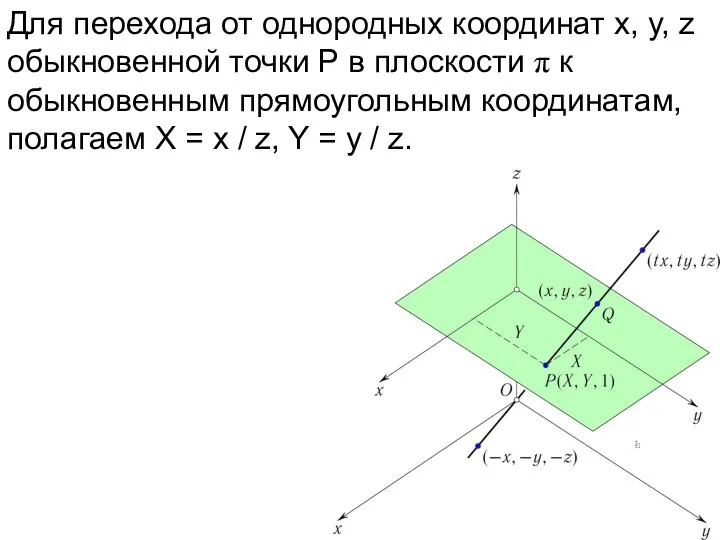
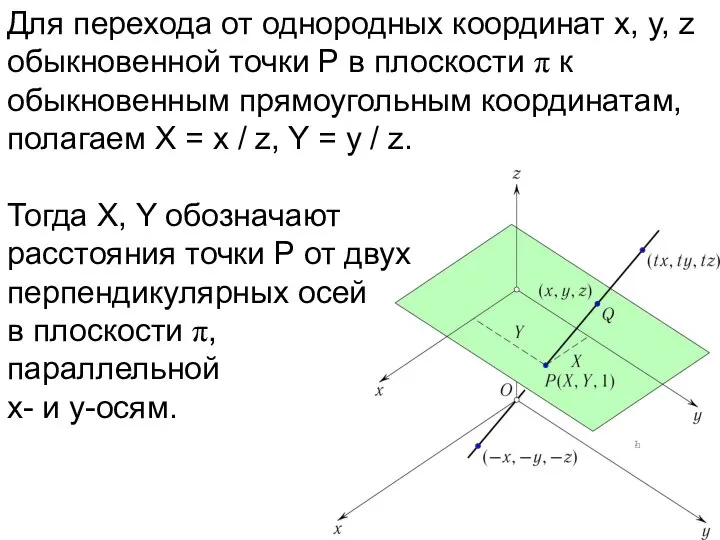
Слайд 51

Для перехода от однородных координат x, y, z обыкновенной точки P

Для перехода от однородных координат x, y, z обыкновенной точки P

в плоскости π к обыкновенным прямоугольным координатам, полагаем X = x / z, Y = y / z.
Слайд 52

Для перехода от однородных координат x, y, z обыкновенной точки P

Для перехода от однородных координат x, y, z обыкновенной точки P

в плоскости π к обыкновенным прямоугольным координатам, полагаем X = x / z, Y = y / z.
Тогда X, Y обозначают
расстояния точки P от двух
перпендикулярных осей
в плоскости π,
параллельной
x- и y-осям.
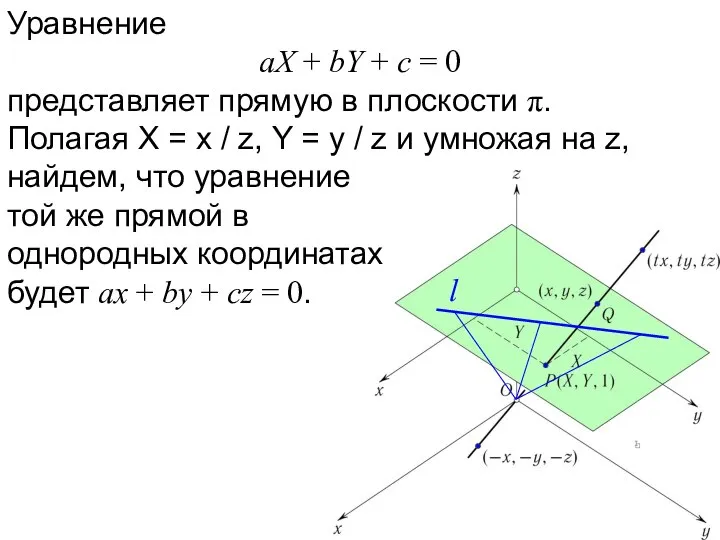
Слайд 53

l Уравнение aX + bY + c = 0 представляет прямую

l

Уравнение
aX + bY + c = 0
представляет прямую в плоскости π.
Полагая

X = x / z, Y = y / z и умножая на z,
найдем, что уравнение той же прямой в однородных координатах будет ax + by + cz = 0.
Слайд 54

Например, уравнение прямой 2x − 3y + z = 0 в

Например, уравнение прямой
2x − 3y + z = 0
в обыкновенных прямоугольных

координатах X, Y примет вид
2X − 3Y + 1 = 0.
Слайд 55

Например, уравнение прямой 2x − 3y + z = 0 в

Например, уравнение прямой
2x − 3y + z = 0
в обыкновенных прямоугольных

координатах X, Y примет вид
2X − 3Y + 1 = 0.
Замечание. Последнему уравнению несобственная точка рассматриваемой прямой с однородными координатами (3, 2, 0) уже не отвечает.
Слайд 56

Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений связывающих

Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений
связывающих однородные

координаты x', y', z�' точек в плоскости π' с однородными координатами x, y, z точек в плоскости π.
Слайд 57

Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений связывающих

Можно показать, что проективное преобразование, задается аналитически системой линейных уравнений
связывающих однородные

координаты x', y', z�' точек в плоскости π' с однородными координатами x, y, z точек в плоскости π.
Тогда теоремы проективной геометрии становятся теоремами о поведении числовых троек (x, y, z) при таких преобразованиях.
Слайд 58

3. Треугольник цветов

3. Треугольник цветов

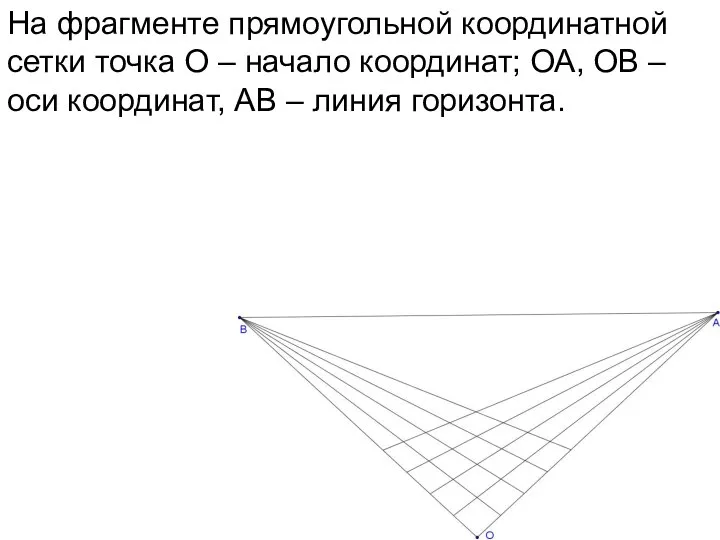
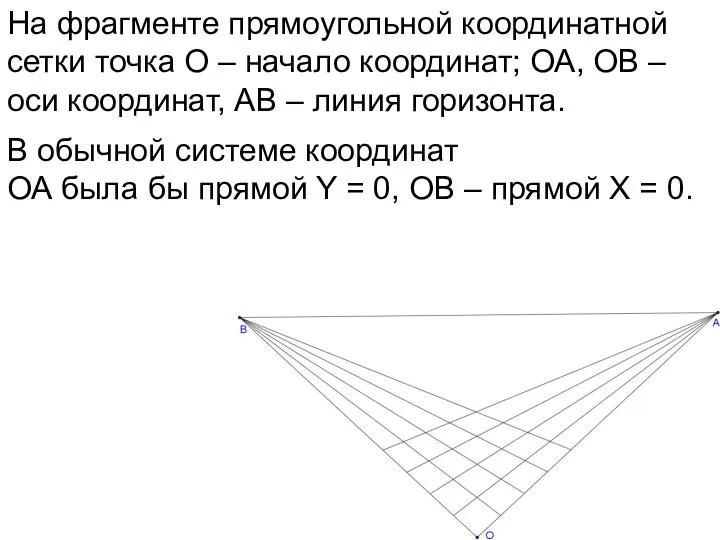
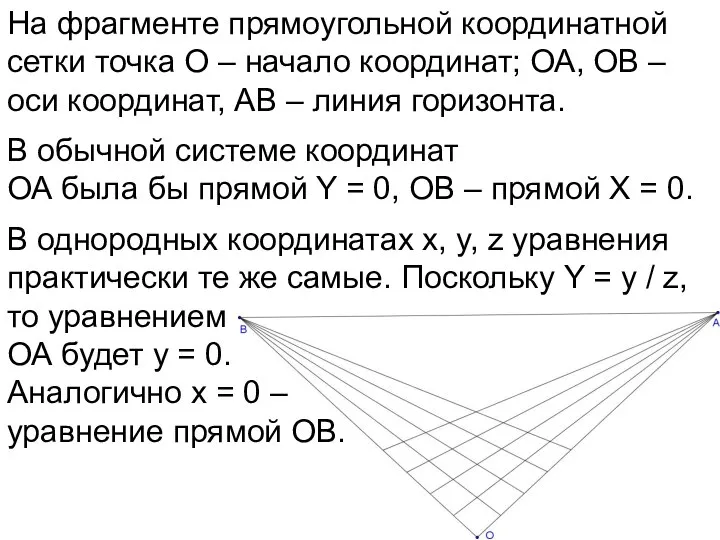
Слайд 59

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

ОВ – оси координат, АВ – линия горизонта.
Слайд 60

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

ОВ – оси координат, АВ – линия горизонта.
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой Х = 0.
Слайд 61

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

На фрагменте прямоугольной координатной сетки точка О – начало координат; ОА,

ОВ – оси координат, АВ – линия горизонта.
В обычной системе координат ОА была бы прямой Y = 0, ОВ – прямой X = 0.
В однородных координатах x, y, z уравнения практически те же самые. Поскольку Y = y / z, то уравнением ОА будет y = 0. Аналогично x = 0 – уравнение прямой ОВ.
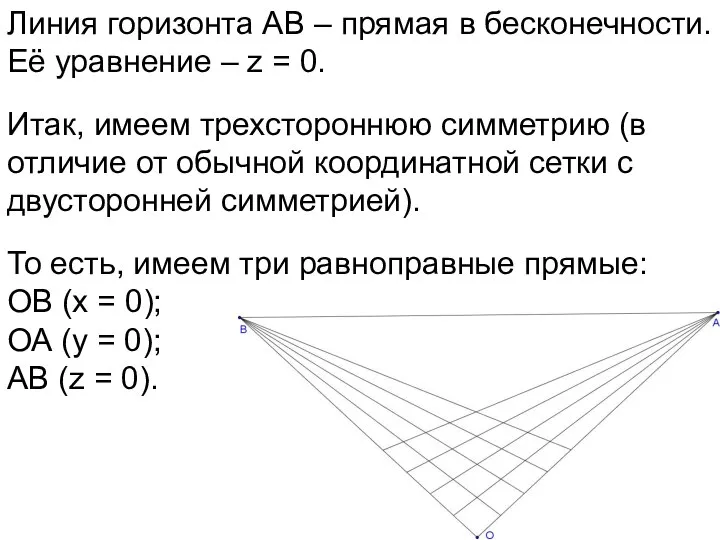
Слайд 62

Линия горизонта АВ – прямая в бесконечности. Её уравнение – z

Линия горизонта АВ – прямая в бесконечности. Её уравнение – z

= 0.
Итак, имеем трехстороннюю симметрию (в отличие от обычной координатной сетки с двусторонней симметрией).
То есть, имеем три равноправные прямые: ОВ (x = 0); ОА (y = 0); АВ (z = 0).
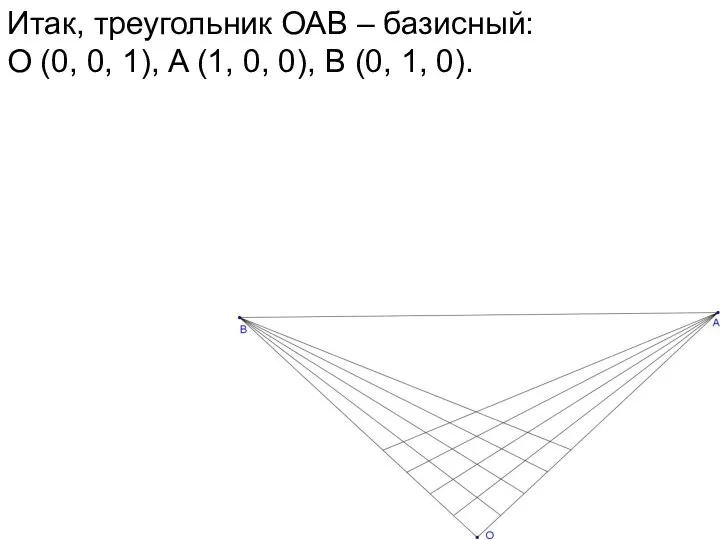
Слайд 63

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1,

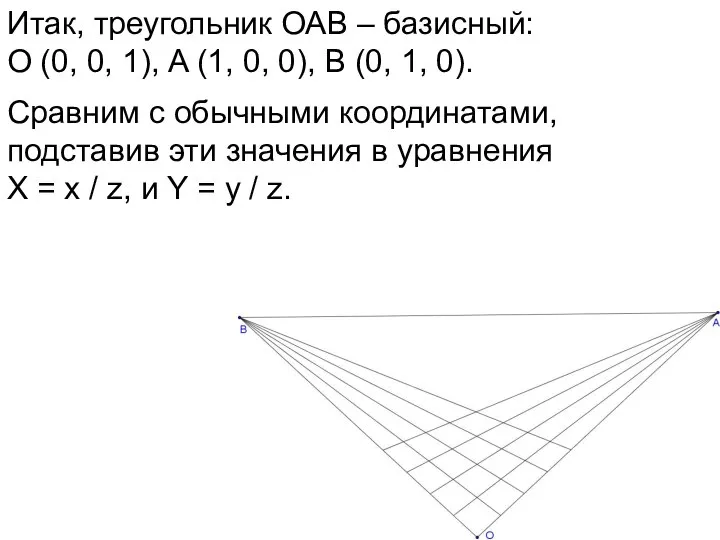
Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,

0), В (0, 1, 0).
Слайд 64

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1,

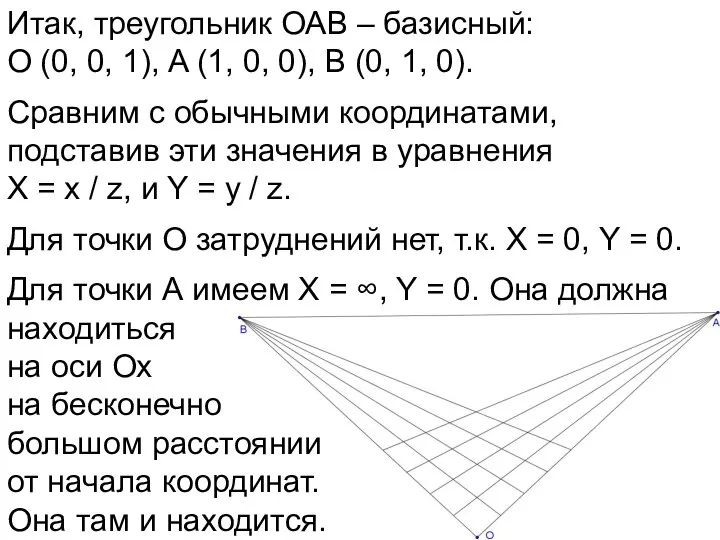
Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,

0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Слайд 65

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1,

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,

0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Слайд 66

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1,

Итак, треугольник ОАВ – базисный: О (0, 0, 1), A (1, 0,

0), В (0, 1, 0).
Сравним с обычными координатами, подставив эти значения в уравнения X = x / z, и Y = y / z.
Для точки О затруднений нет, т.к. Х = 0, Y = 0.
Для точки А имеем X = ∞, Y = 0. Она должна находиться на оси Ох на бесконечно большом расстоянии от начала координат. Она там и находится.
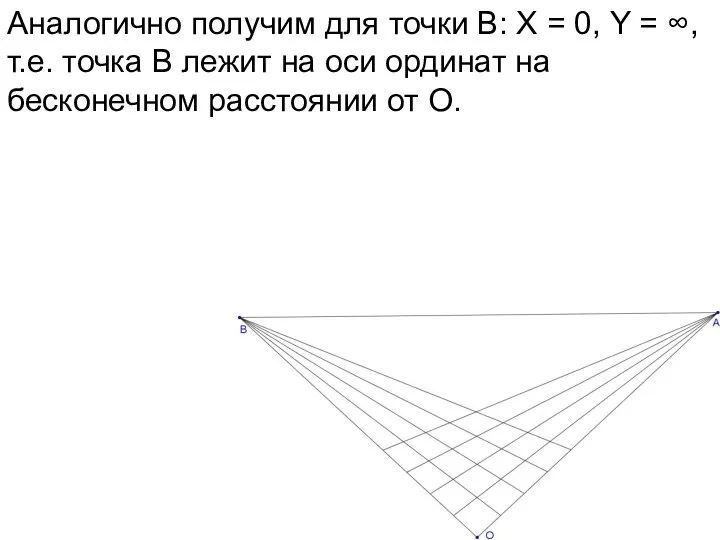
Слайд 67

Аналогично получим для точки В: Х = 0, Y = ∞,

Аналогично получим для точки В: Х = 0, Y = ∞,

т.е. точка В лежит на оси ординат на бесконечном расстоянии от О.
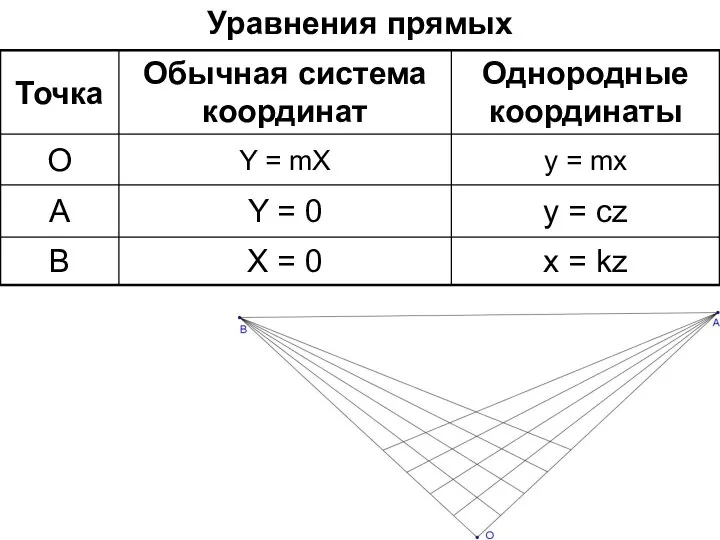
Слайд 68

Уравнения прямых

Уравнения прямых

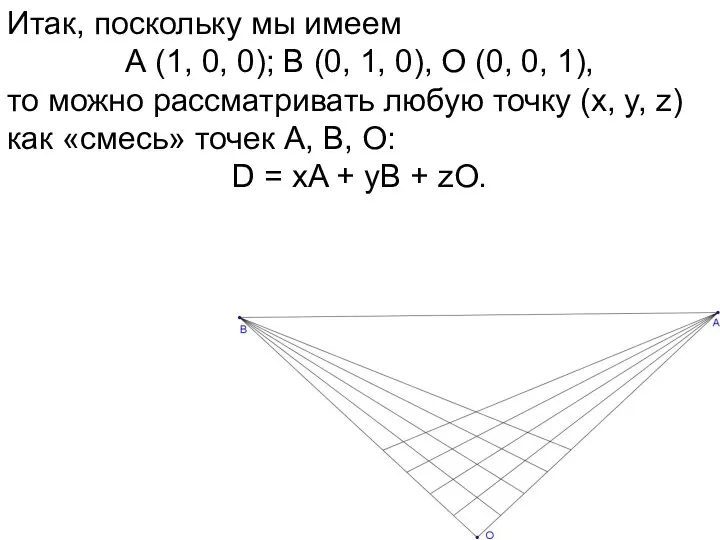
Слайд 69

Итак, поскольку мы имеем А (1, 0, 0); В (0, 1,

Итак, поскольку мы имеем
А (1, 0, 0); В (0, 1, 0),

О (0, 0, 1),
то можно рассматривать любую точку (x, y, z) как «смесь» точек А, В, О:
D = xA + yB + zO.
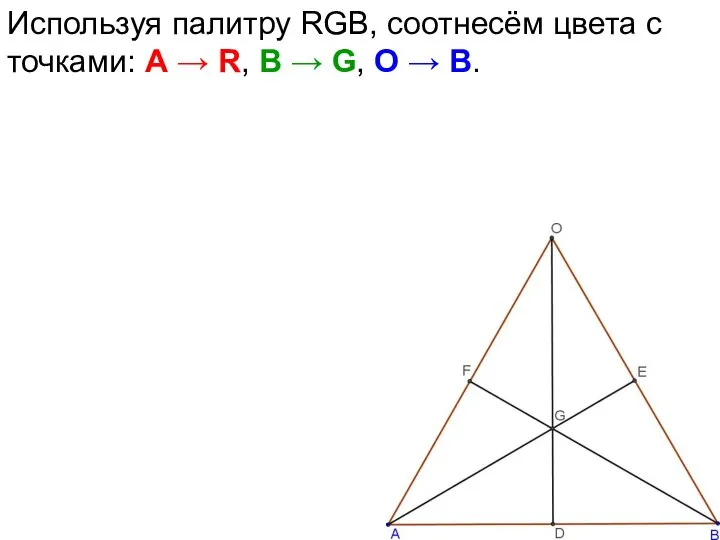
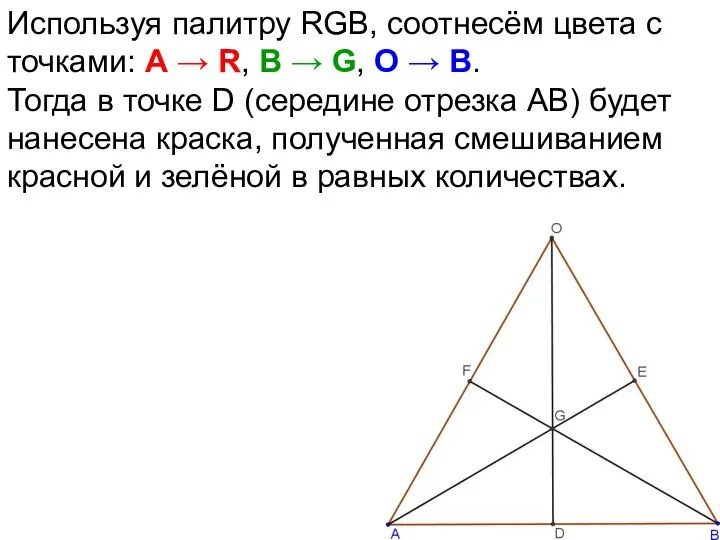
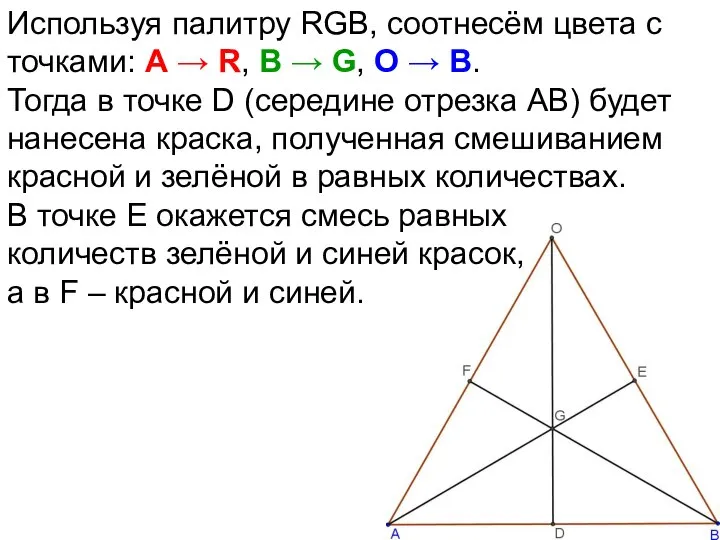
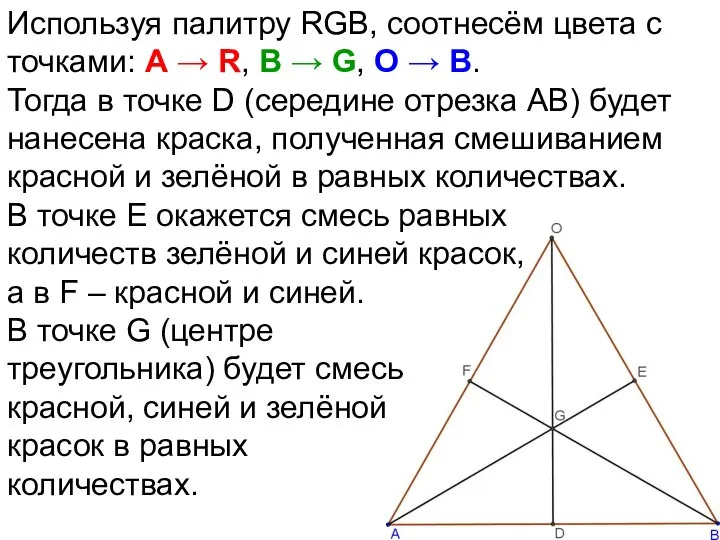
Слайд 70

Используя палитру RGB, соотнесём цвета с точками: А → R, В → G, О → B.

Используя палитру RGB, соотнесём цвета с точками: А → R, В

→ G, О → B.
Слайд 71

Используя палитру RGB, соотнесём цвета с точками: А → R, В

Используя палитру RGB, соотнесём цвета с точками: А → R, В

→ G, О → B. Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах.
Слайд 72

Используя палитру RGB, соотнесём цвета с точками: А → R, В

Используя палитру RGB, соотнесём цвета с точками: А → R, В

→ G, О → B. Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах. В точке Е окажется смесь равных количеств зелёной и синей красок, а в F – красной и синей.
Слайд 73

Используя палитру RGB, соотнесём цвета с точками: А → R, В

Используя палитру RGB, соотнесём цвета с точками: А → R, В

→ G, О → B. Тогда в точке D (середине отрезка АВ) будет нанесена краска, полученная смешиванием красной и зелёной в равных количествах. В точке Е окажется смесь равных количеств зелёной и синей красок, а в F – красной и синей. В точке G (центре треугольника) будет смесь красной, синей и зелёной красок в равных количествах.
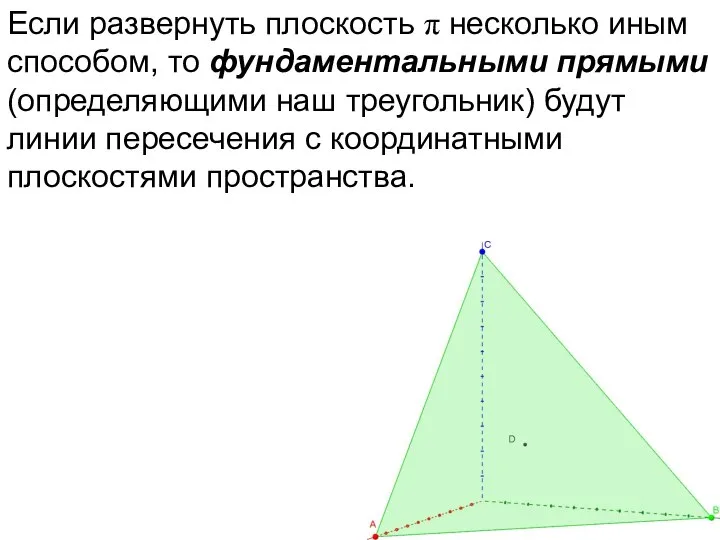
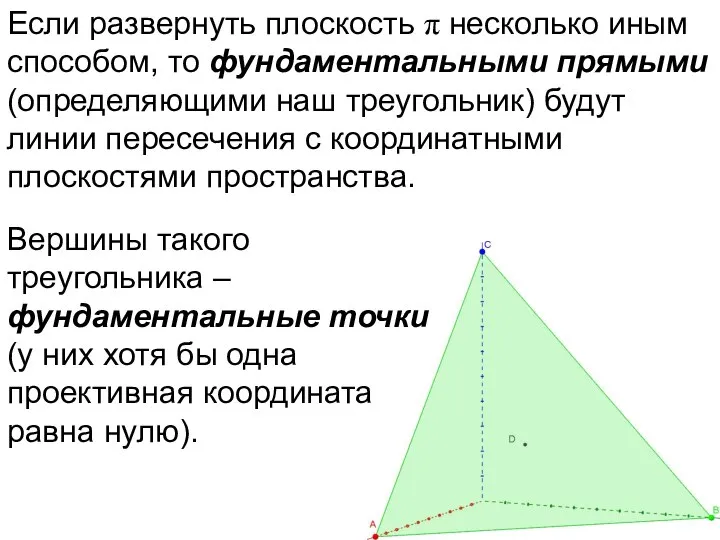
Слайд 74

Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими

Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими

наш треугольник) будут линии пересечения с координатными плоскостями пространства.
Слайд 75

Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими

Если развернуть плоскость π несколько иным способом, то фундаментальными прямыми (определяющими

наш треугольник) будут линии пересечения с координатными плоскостями пространства.
Вершины такого треугольника – фундаментальные точки (у них хотя бы одна проективная координата равна нулю).
- Предыдущая
Исследования полотна автомобильных дорог
Следующая -
Краткий обзор оборудования

Похожие презентации

Степень степени, произведения и дроби
Сложение и вычитание трехзначных чисел
Презентация по математике "Параллельные прямые в пространстве" - скачать
Четные и нечетные функции. 10 класс
Параллельный перенос
Приемы быстрого счета
Рациональные уравнения как математические модели реальных ситуаций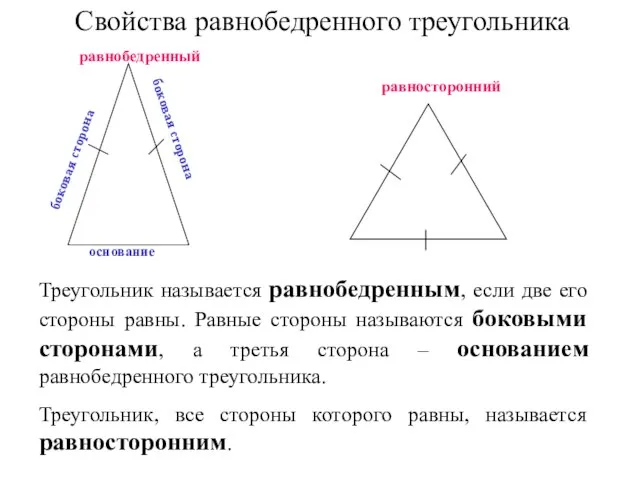
Свойства равнобедренного треугольника
Квадратные уравнения
Основное свойство дроби
Параллельные плоскости. Задачи
Скалярное произведение векторов. (Лекция 5)
Математика 3 класс. Тема. Умножение и деление. Цель: закреплять навыки умножения и деления.
Неполные квадратные уравнения
Числа вокруг нас
Тип игры: викторина Автор: Панфилова Ольга Юрьевна учитель математики МКОУ «Петуховская средняя общеобразовательная школа №1
Центральные и вписанные углы
Сложение и вычитание смешанных чисел. 5 класс
Поділ числа в заданому відношенні. Масштаб
Решение задач на составление уравнений
ЭЛЕКТИВНЫЙ КУРС «Алгебра функций» Выполнила: Винник Н.А.- учитель математики 435 школы
Определение и основные свойства множеств
Степень с натуральным, целым и рациональным показателем. Свойства степеней
Урок математики в 1 классе. Решение задач на сравнение
Рациональные вычисления
Производная функции в точке
Теория вероятности
Теорема Пифагора. И её доказательства.
Вы можете прислать нам Вашу презентацию и мы опубликуем ее на сайте.
Обратная связь
Для правообладателей
Email: Нажмите что бы посмотреть