Содержание
- 2. «Кто смолоду делает и думает сам, тот становиться потом, надежнее, крепче, умнее» В. Шукшин.
- 3. Монотонность функции Если производная функции y=f(x) положительна на некотором интервале, то функция на этом интервале монотонно
- 4. Экстремумы функции Определение 1. Точку х=х0 называют точкой минимума функции f(х), если у этой точки существует
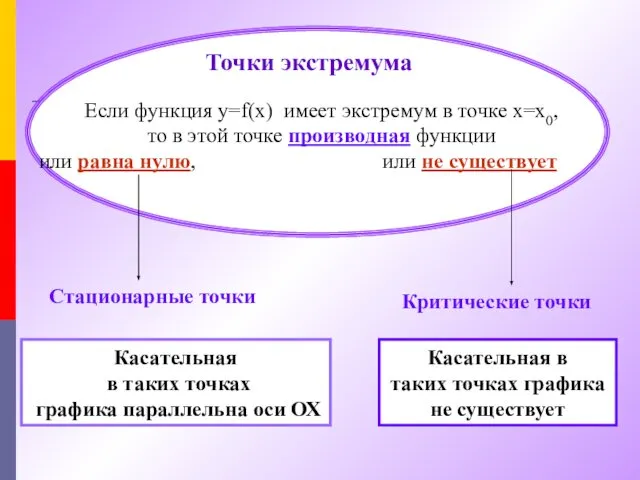
- 5. Точки экстремума Стационарные точки Критические точки Если функция y=f(x) имеет экстремум в точке x=x0, то в
- 6. Достаточное условие существования экстремума функции: Если при переходе через критическую точку х0 функции f(x) ее производная
- 7. Исследование функции на монотонность Найти производную f ´. Решить уравнение f ´(х)=0. Отметить найденные точки на
- 8. Вычисляем производную : y’=6x²-6x-36. Находим критические точки: y’=0. x²-x-6=0 Д=1-4*(-6)*1=1+24=25 Отмечаем точки на числовой прямой и
- 9. Алгоритм исследования функции f(х) на экстремум с помощью производной : Найти производную f ´ Решить уравнение
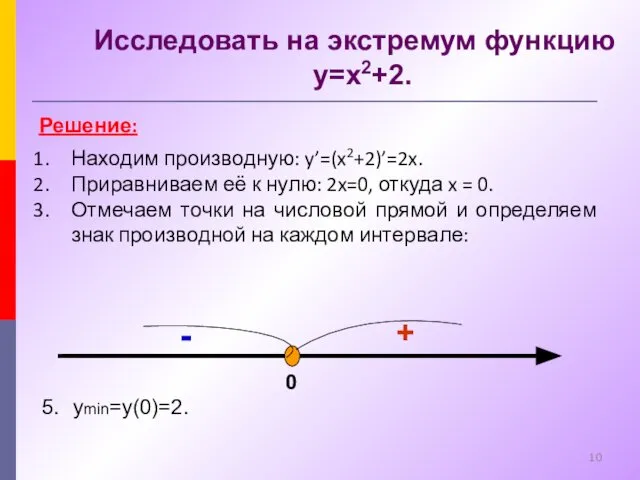
- 10. Исследовать на экстремум функцию y=x2+2. Решение: Находим производную: y’=(x2+2)’=2x. Приравниваем её к нулю: 2x=0, откуда x
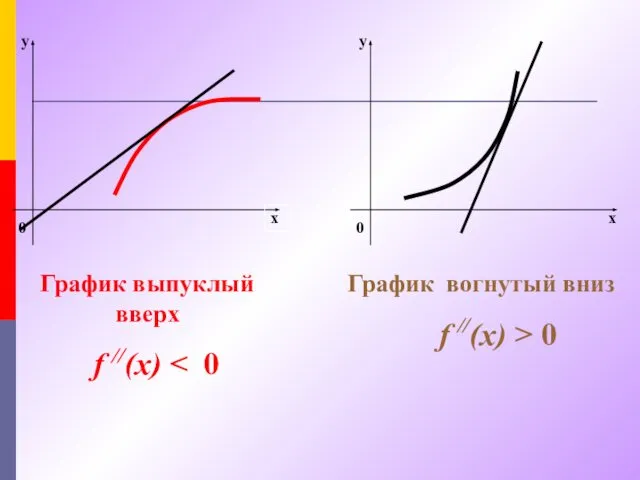
- 11. Если функция f(x) имеет на интервале (a,b) вторую производную и f''(x)≥0 (f''(x)≤0) во всех точках (a,b),
- 12. График выпуклый вверх f //(x) График вогнутый вниз f //(x) > 0
- 14. Скачать презентацию








 Решение матричных игр в смешанных стратегиях 2xn и mx2
Решение матричных игр в смешанных стратегиях 2xn и mx2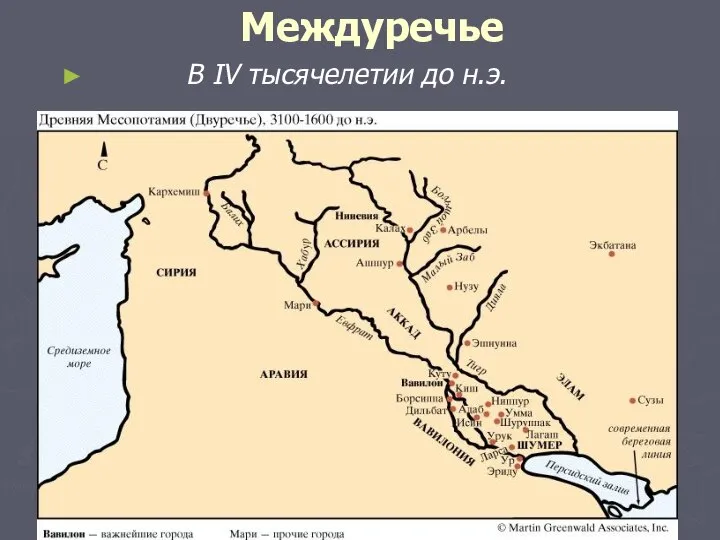 Междуречье В IV тысячелетии до н.э.
Междуречье В IV тысячелетии до н.э. Задачи на проценты
Задачи на проценты Фестиваль педагогических идей «Открытый урок» Конкурс «Презентация к уроку» Тема: Геометрические фигуры. 5 класс
Фестиваль педагогических идей «Открытый урок» Конкурс «Презентация к уроку» Тема: Геометрические фигуры. 5 класс  Сравнение дробей
Сравнение дробей Сложные суждения. (Тема 4)
Сложные суждения. (Тема 4) Признаки равенства треугольников
Признаки равенства треугольников Состав чисел от 2 до 10
Состав чисел от 2 до 10 Деление с остатком
Деление с остатком Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1)
Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1) Приёмы устных вычислений (урок 116)
Приёмы устных вычислений (урок 116) Применение распределительного свойства умножения. 6 класс
Применение распределительного свойства умножения. 6 класс Перестановки и размещения
Перестановки и размещения Пропорція. Основна властивість пропорції
Пропорція. Основна властивість пропорції Непрерывность функции одной переменной
Непрерывность функции одной переменной Многогранники. Правильные многогранники
Многогранники. Правильные многогранники Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Квадратурные формулы Ньютона-Котеса
Квадратурные формулы Ньютона-Котеса Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса
Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса Цилиндр, конус, шар
Цилиндр, конус, шар Model Parameterization in tomography problems. Lecture 4
Model Parameterization in tomography problems. Lecture 4 Конус
Конус Однофакторні нелінійні економетричні моделі
Однофакторні нелінійні економетричні моделі последовательности и Династия Романовых
последовательности и Династия Романовых  Функция распределения случайной величины
Функция распределения случайной величины Признаки параллельности прямых
Признаки параллельности прямых Симметрия вокруг нас
Симметрия вокруг нас