Содержание
- 2. Задача расширения понятия числа Положительные рациональные числа Действительные числа
- 3. Задача расширения понятия числа Большинство применений математики сводится к двум основным задачам: - подсчет числа элементов
- 5. 4 куска ткани
- 6. Для решения первой задачи достаточно множества целых неотрицательных чисел: N0 = {0, 1, 2, 3, …}
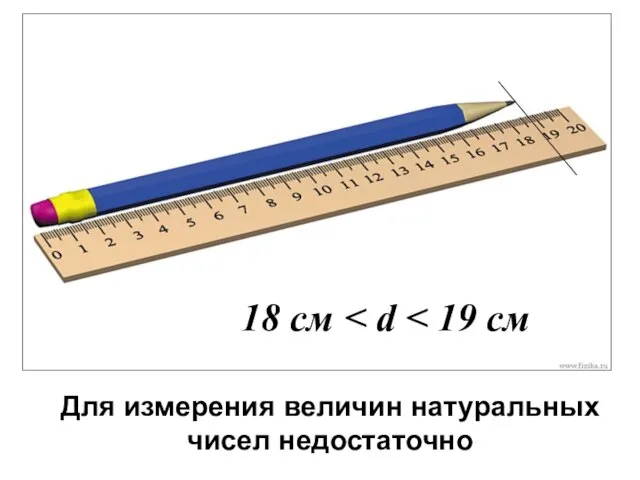
- 7. 18 см Для измерения величин натуральных чисел недостаточно
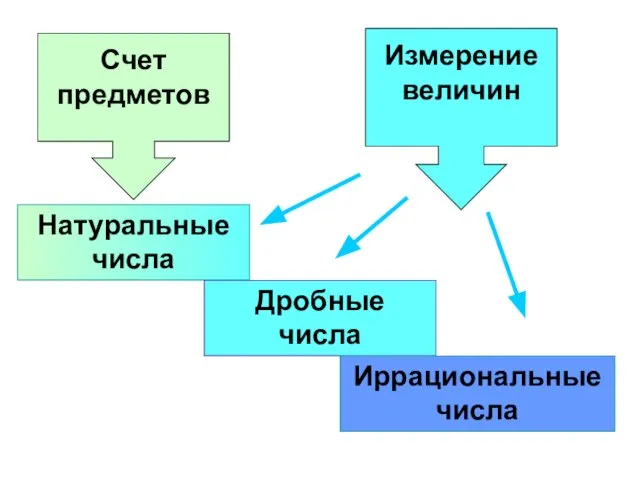
- 8. Натуральные числа Дробные числа Иррациональные числа
- 9. Q Взаимосвязи между числовыми множествами R Z
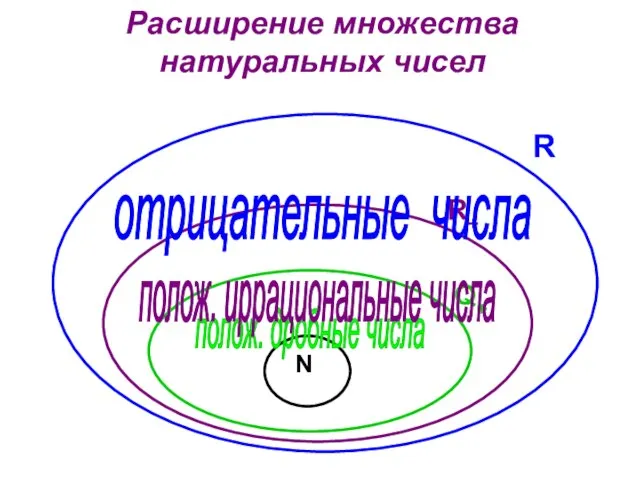
- 10. Q+ Расширение множества натуральных чисел R+ R
- 11. ПОЛОЖИТЕЛЬНЫЕ РАЦИОНАЛЬНЫЕ ЧИСЛА Понятие дроби Понятие положительного рационального числа Арифметические действия над положительными рациональными числами Свойства
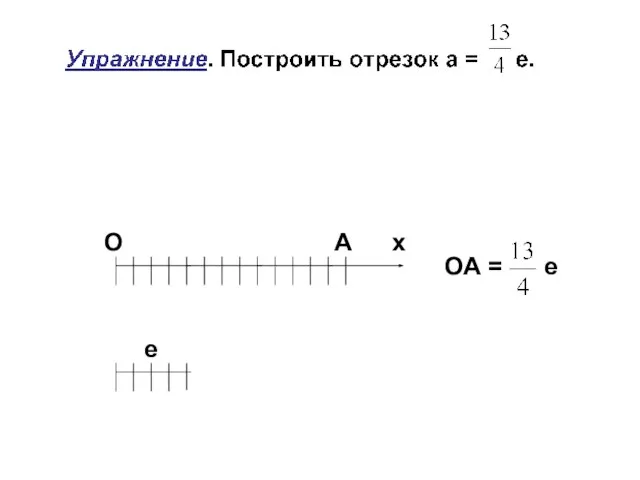
- 12. Понятие дроби Дан отрезок а, выберем единичный отрезок е. При измерении длины отрезка а могут возникнуть
- 14. Длина отрезка а при единице длины е выражается обыкновенной дробью Отрезки а и е в этом
- 15. 3. Единичный отрезок е и любая его часть не укладываются в отрезке а целое число раз.
- 16. Рассмотрим отрезок а, выберем единичный отрезок е
- 18. Дроби, выражающие длину одного и того же отрезка при единице длины е, называют равными дробями (или
- 20. Основное свойство дроби На этом свойстве основано сокращение дробей и приведение дробей к общему знаменателю
- 21. Сокращение дроби – это замена данной дроби другой, равной данной, но с меньшим числителем и знаменателем
- 22. Пример 1: несократимая дробь, т. к. D (5; 17) = 1, т.е. 5 и 17 взаимно
- 23. Приведение дробей к общему знаменателю – это замена данных дробей равными им дробями, имеющими одинаковые знаменатели
- 24. 15 = 3 · 5, 35 = 5 · 7, K(15, 35) = 3 · 5
- 25. Дробь называется правильной, если её числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или
- 27. Понятие положительного рационального числа
- 28. - Обыкновенная дробь, числитель, знаменатель - Правильная дробь - Неправильная дробь - Сократимая дробь - Несократимая
- 29. Одному и тому же отрезку можно поставить в соответствие бесконечное множество равных дробей, выражающих его длину
- 30. Положительным рациональным числом называется класс равных дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление)
- 36. Арифметические действия над положительными рациональными числами
- 37. Сложение Рассмотрим отрезки а, b и с, е – единичный отрезок mе1 + ре1 = (m
- 38. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их
- 39. Чтобы сложить дроби, нужно привести их к общему знаменателю, затем сложить их числители и полученную сумму
- 40. В общем виде правило сложения можно записать так: Если D(n, q) = 1, К(n, q) =
- 41. Теорема (о существовании и единственности суммы) Сумма любых двух положительных рациональных чисел существует и единственна
- 42. Отношение «больше» Пусть а, b ∈ Q+. Определение. Число а больше числа b, если существует такое
- 43. Практические приемы установления отношения «больше»
- 44. Теорема. (∀ а, b ∈ Q+) а ≠ b ⇒ а > b ∨ b >
- 45. Отношение «больше» обладает свойствами: 1) антисимметричности: 2) транзитивности: (∀ а, b, с ∈ Q+) а >
- 46. 2) Ассоциативный закон сложения (∀ а, b, с ∈ Q+) (а + b) + с =
- 47. 5) (∀ а, b ∈ Q+) а + b ≠ а 6) (∀ а ∈ Q+)
- 52. Разностью положительных рациональных чисел а и b называется такое положительное рациональное число с, что а =
- 53. Теорема (о существовании и единственности разности) Разность а – b положительных рациональных чисел существует тогда и
- 55. Правила вычитания 1) правило вычитания числа из суммы а > с ⇒ (а + b) –
- 56. 2) правило вычитания суммы из числа а – (b + с) = (а – b) –
- 57. Умножение
- 58. Примеры: 1)
- 59. Теорема (о существовании и единственности произведения) Произведение любых двух положительных рациональных чисел существует и единственно
- 60. 2) Ассоциативный закон умножения (∀ а, b, с ∈ Q+) (а · b) · с =
- 61. 5) Сократимость умножения (∀ а, b, с ∈ Q+) а · с = b · с
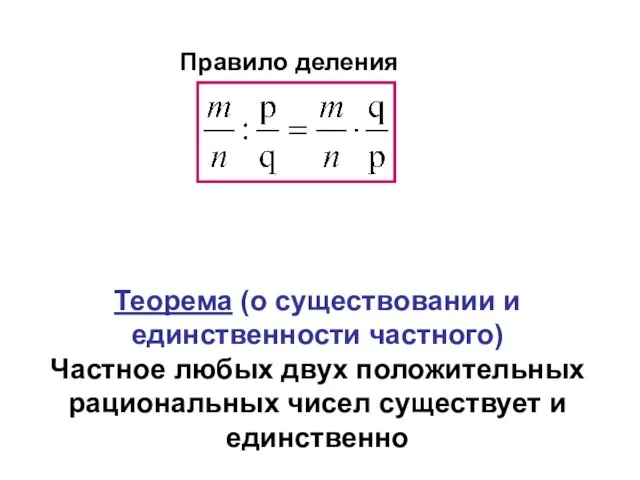
- 62. Деление Частным положительных рациональных чисел а и b называется такое положительное рациональное число с, что а
- 63. Теорема (о существовании и единственности частного) Частное любых двух положительных рациональных чисел существует и единственно Правило
- 64. 2) правило деления числа на произведение а : (b · с) = а : b :
- 65. 5) а : 1 = а, а : а = 1 а · 0 = 0
- 66. Термин «рациональное число» произошел от латинского слова r а t i о, что в переводе на
- 67. СВОЙСТВА МНОЖЕСТВА ПОЛОЖИТЕЛЬНЫХ РАЦИОНАЛЬНЫХ ЧИСЕЛ 1. N ⊂ Q+
- 68. 2. Множество Q+ не ограничено снизу, т.е. в нем нет наименьшего числа 3. Множество Q+ не
- 69. 5. Множество Q+ плотно, т.е. между любыми двумя различными числами а и b из Q+ заключено
- 70. Основные задачи на дроби 1.Нахождение дроби от числа
- 71. 2.Нахождение числа по данному значению дроби
- 72. 3.Нахождение отношения двух чисел В классе 25 учеников. 10 учеников ходили в кино. Какую часть всех
- 73. Проценты Чтобы проценты выразить дробью, нужно число процентов разделить на 100 и отбросить знак %. Чтобы
- 74. Основные задачи на проценты В классе 25 учеников. 40 % учащихся класса ходили в кино. Сколько
- 75. 10 учеников класса ходили в кино, что составляет 40 % всех учащихся класса. Сколько всего учеников
- 76. 3.Нахождение процентного отношения двух чисел В классе 25 учеников. 10 учеников ходили в кино. Сколько процентов
- 77. Множество положительных рациональных чисел как расширение множества натуральных чисел Условия расширения: 1. N ⊂ Q+ 2.
- 78. 3. Выполнимость в Q+ операции, не всегда осуществимой в N Деление, которое не всегда выполняется во
- 79. Упражнение Решить уравнение, используя зависимость между компонентами и результатами действий:
- 80. Десятичные дроби
- 81. Примеры:
- 82. Утверждение: Если к десятичной дроби А,an-1 ... a0 приписать справа любое число нулей, то получится десятичная
- 83. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД ДЕСЯТИЧНЫМИ ДРОБЯМИ Сложение и вычитание
- 84. Умножение Примеры: 1) 5,426·102 = 542,6 2) 5,42·103 = 5420
- 85. 24,48 : 1,2 = 244,8 : 12 = 20,4 Примеры: 1) 24 4 2 0, 8
- 86. ПЕРЕВОД ОБЫКНОВЕННЫХ ДРОБЕЙ В ДЕСЯТИЧНЫЕ И ДЕСЯТИЧНЫХ – В ОБЫКНОВЕННЫЕ
- 87. ? Чтобы перевести обыкновенную дробь в десятичную, нужно разделить числитель на знаменатель
- 89. Примеры: 1) 0,04375
- 90. - дробь нельзя превратить в конечную десятичную 0,75 260 = 22 · 5 · 13
- 91. Упражнения
- 94. БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ПЕРИОДИЧЕСКИЕ ДРОБИ 1,42857141… = = 1,(42857141) Пример 1
- 95. 2,8181… = = 2,(81) Пример 2
- 96. 4,4166… = = 4,41(66) Пример 3
- 97. Пример 4 0,25 = 0,250000…. = 0,25(0) Дробь называется периодической, если начиная с некоторой цифры, она
- 98. Если период следует сразу после запятой, то такую дробь называют чисто периодической. Если перед периодом стоят
- 99. Чисто периодическая бесконечная десятичная дробь, меньше единицы, равна такой обыкновенной дроби, числитель которой равен периоду, а
- 100. Смешанная периодическая дробь, меньше единицы, равна такой обыкновенной дроби, числитель которой равен разности между числом, записанным
- 103. Скачать презентацию























































































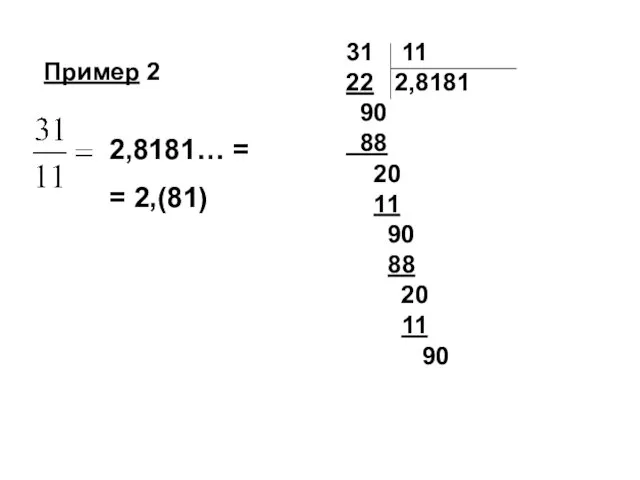






 Линейные регрессионные модели с гетероскедастичными остатками
Линейные регрессионные модели с гетероскедастичными остатками Основы математического планирования эксперимента
Основы математического планирования эксперимента Аттестационная работа. Все профессии важны, с математикой дружны
Аттестационная работа. Все профессии важны, с математикой дружны Деление многозначного на трехзначное
Деление многозначного на трехзначное Основные тригонометрические формулы
Основные тригонометрические формулы Геометрическая прогрессия
Геометрическая прогрессия Все об окружности
Все об окружности Правильные многогранники (симметрия) 10 класс
Правильные многогранники (симметрия) 10 класс Презентация по математике "Простые и составные числа" - скачать бесплатно
Презентация по математике "Простые и составные числа" - скачать бесплатно Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Окружность. Центральные и вписанные углы. Решение задач на готовых чертежах
Окружность. Центральные и вписанные углы. Решение задач на готовых чертежах Математическая игра «Что? Где? Когда?»
Математическая игра «Что? Где? Когда?» Гетероскедастичность. Предпосылки МНК, связанные с ошибками
Гетероскедастичность. Предпосылки МНК, связанные с ошибками Методы параллельных вычислений
Методы параллельных вычислений Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Части графа. Операции над частями графа
Части графа. Операции над частями графа Частные производные функции нескольких переменных
Частные производные функции нескольких переменных МОУ «Средняя общеобразовательная школа №11» с. Юца, Предгорного района Ставропольского края Интегрированный урок (технологи
МОУ «Средняя общеобразовательная школа №11» с. Юца, Предгорного района Ставропольского края Интегрированный урок (технологи Формулы сокращенного умножения
Формулы сокращенного умножения Площадь прямоугольника. Разработка проекта учебного занятия по математике в 5 классе
Площадь прямоугольника. Разработка проекта учебного занятия по математике в 5 классе Принципы проектирования комбинационных логических схем
Принципы проектирования комбинационных логических схем В мире единиц длины
В мире единиц длины Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве
Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве Методы прогнозирования динамики экономических процессов
Методы прогнозирования динамики экономических процессов Одночлен и его стандартный вид. 7 класс
Одночлен и его стандартный вид. 7 класс Симплекс. Симплексное планирование
Симплекс. Симплексное планирование Заинька. Математическая раскраска. Реши примеры и покажи ответы
Заинька. Математическая раскраска. Реши примеры и покажи ответы