Содержание
- 3. Возможны следующие случаи:
- 5. Пример . Решение. Найти общее решение НЛДУ
- 6. Найдем А. Подставим в уравнение: Общее решение НЛДУ:
- 8. Чтобы получить тождество многочленов,
- 9. Пример . Решение. Найти общее решение НЛДУ
- 10. Найдем А.
- 12. Возможны следующие случаи:
- 13. Замечание.
- 14. Пример . Решение. Найти общее решение НЛДУ
- 15. Найдем А и В.
- 17. Пример . Решение. Найти общее решение НЛДУ
- 18. Найдем А и В.
- 20. тогда частное решение НЛДУ равно сумме этих двух решений
- 21. непрерывные функции или постоянные. Пусть общее решение соответствующего однородного уравнения
- 22. Частное решение НЛДУ ищется в виде: функции, определяемые из системы уравнений
- 23. возможны следующие случаи: Метод неопределенных коэффициентов
- 25. Пример . Решение. Найти общее решение НЛДУ
- 28. Возможны следующие случаи:
- 30. Пример . Решение. Найти общее решение НЛДУ
- 31. Найдем А и В.
- 34. Определение. Если p1 = p2 = … = pn = 1, то система (1) называется нормальной.
- 35. Решением системы (2) на (a,b) называется совокупность функций y1 = у1(х), у2 = у2(х), … ,
- 36. ДУ n-го порядка всегда можно свести к нормальной системе. Систему ДУ, записанную в каноническом виде всегда
- 37. Пример. – каноническая система четвертого порядка. Обозначим: y1' = у3, у2' = у4. Тогда – нормальная
- 38. Задача Коши для нормальной системы Даны система ДУ (2) и начальные условия y1(x0) = y10,..., yn(x0)
- 40. Скачать презентацию



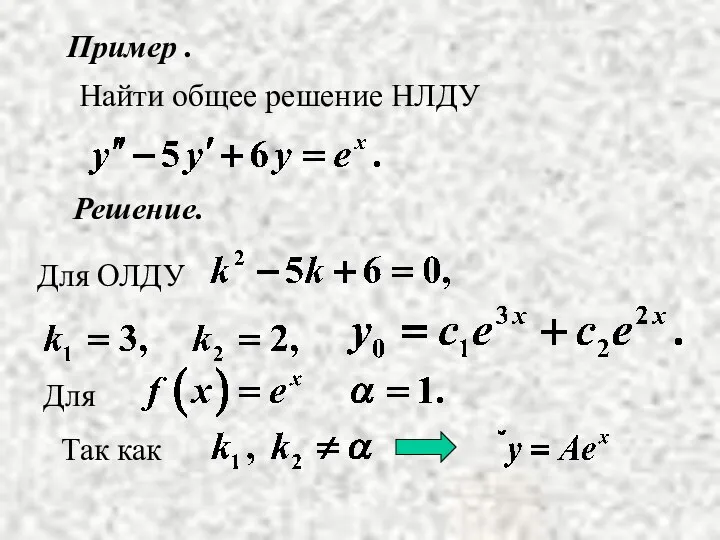



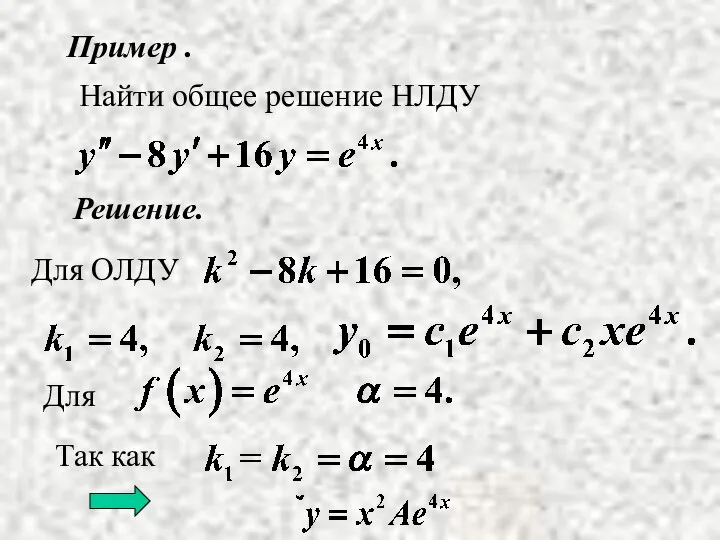
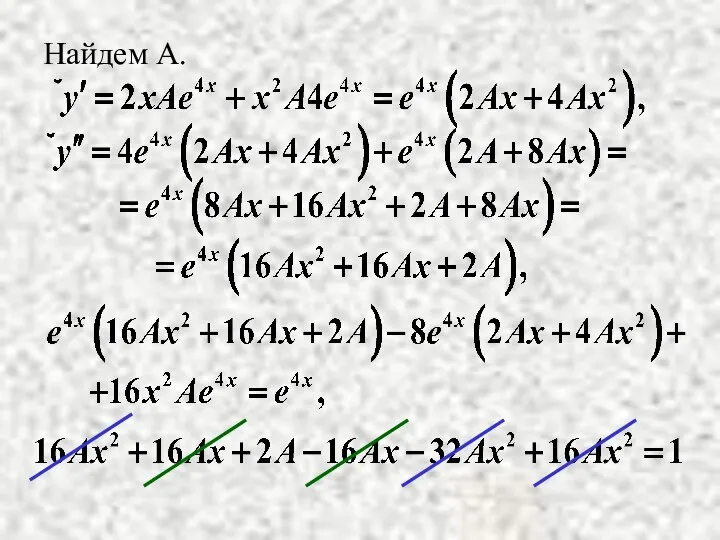
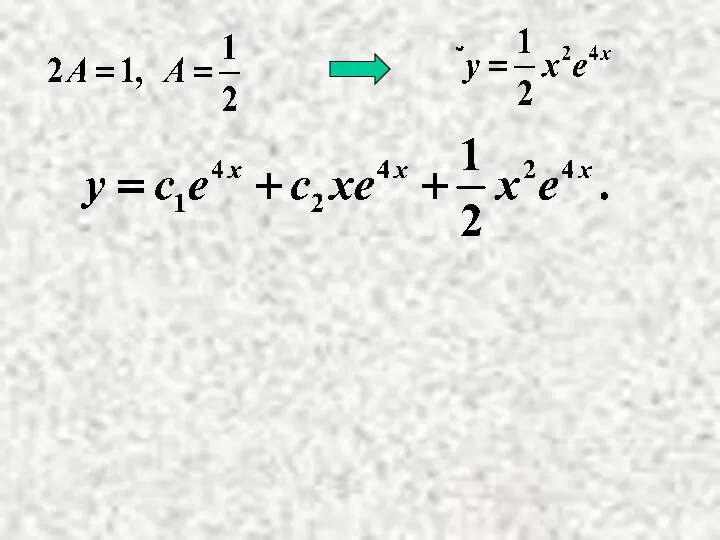


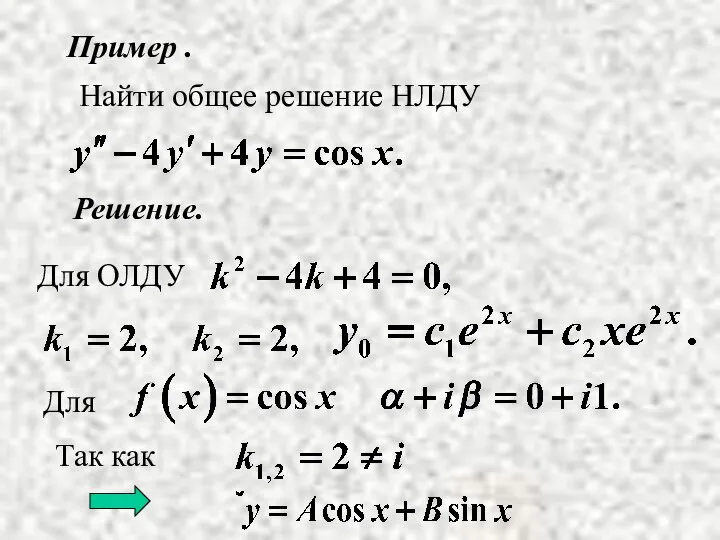
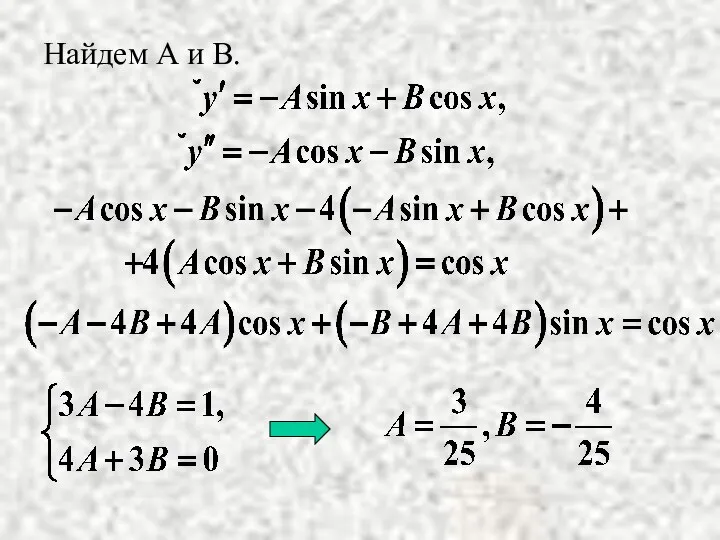
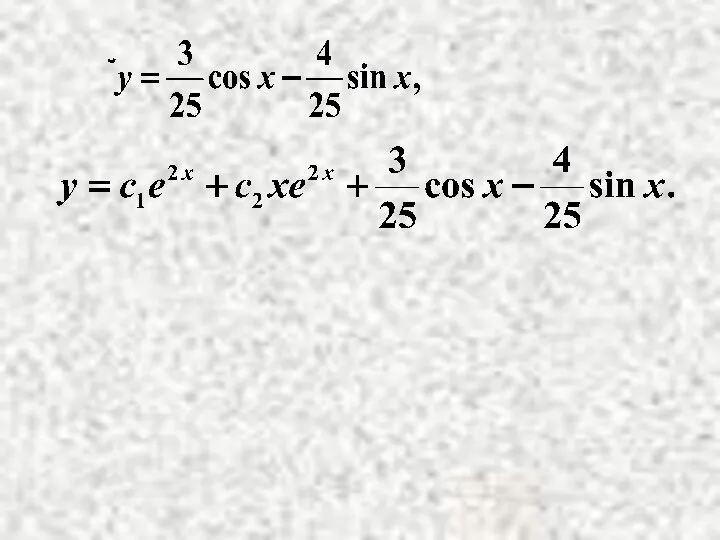
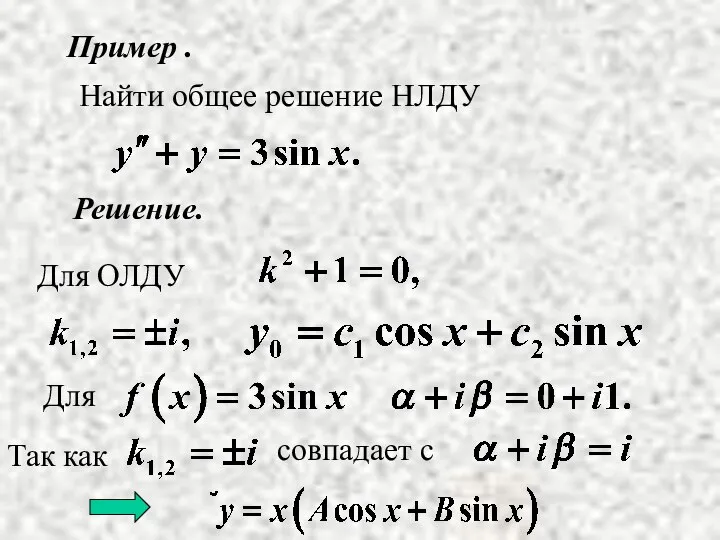
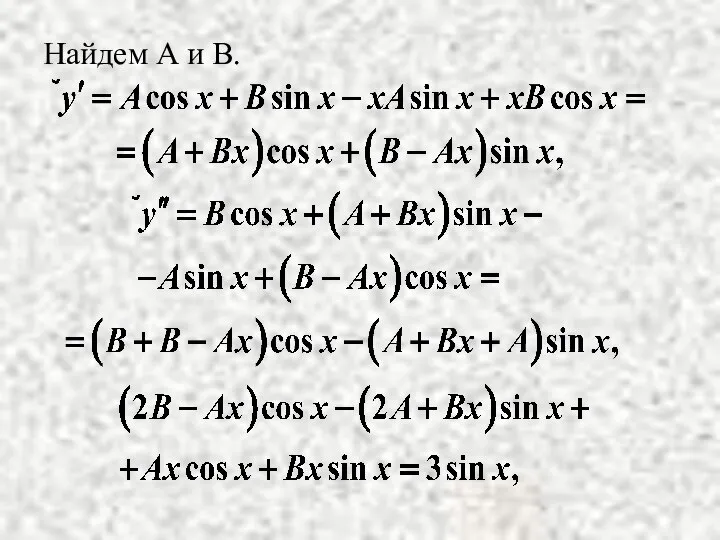
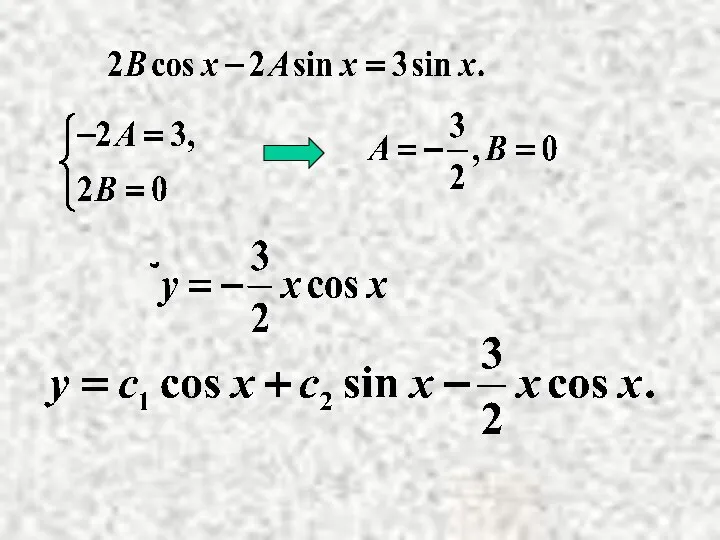





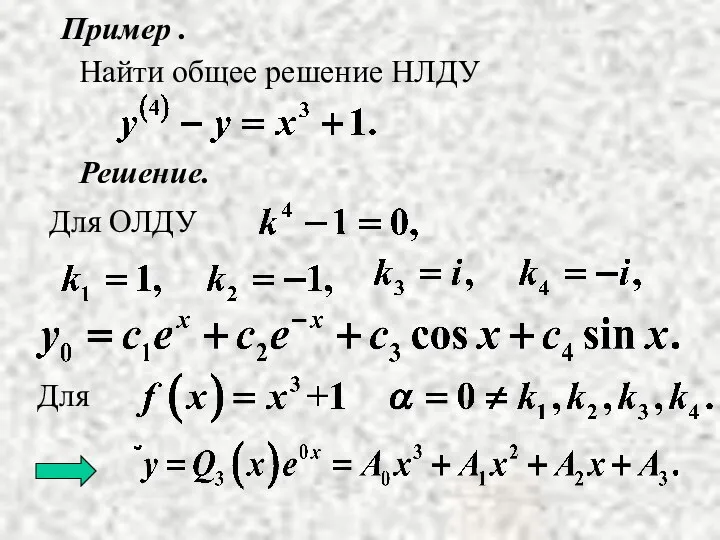

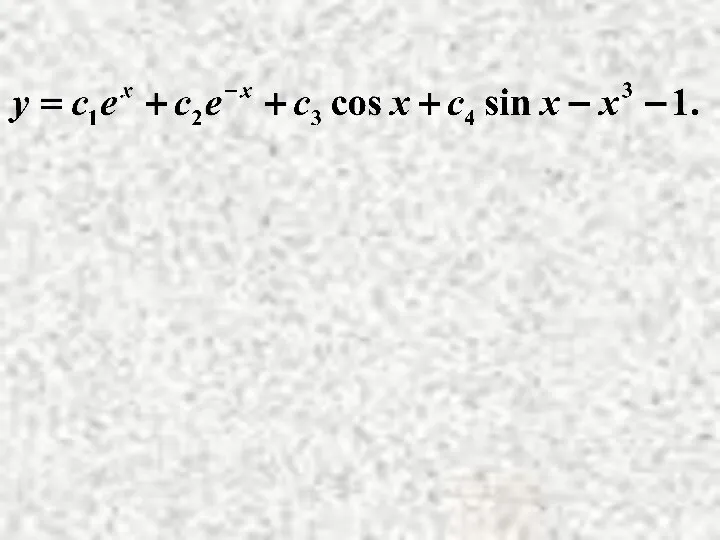


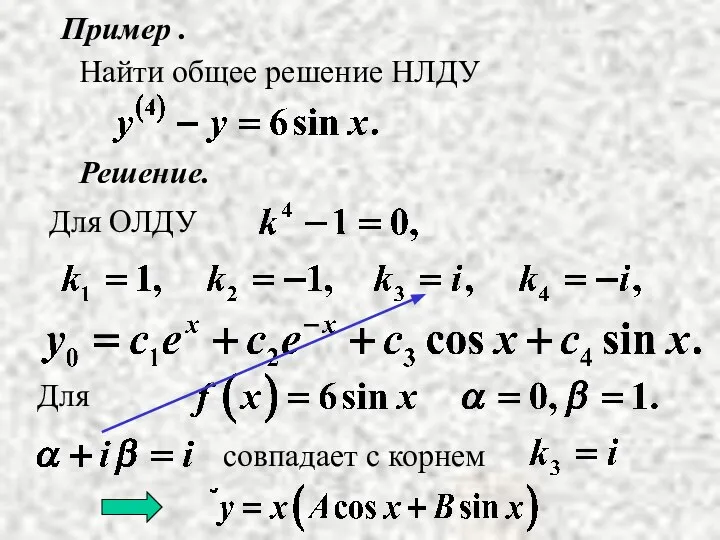
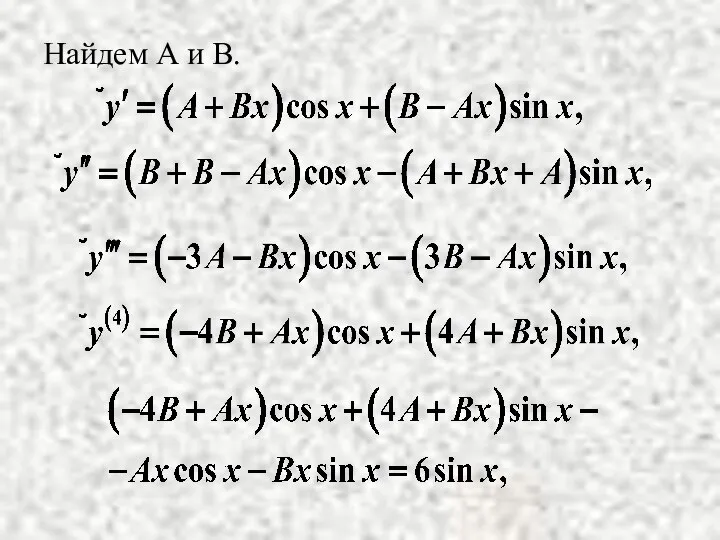
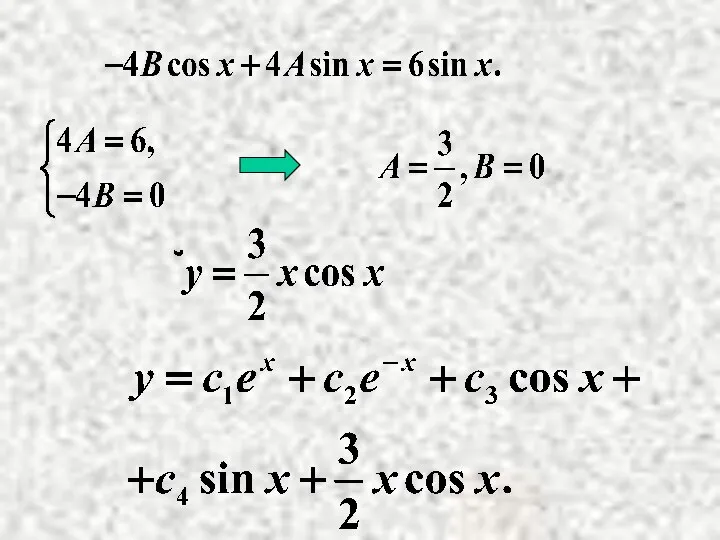






 Проект: Веселый счет 1 класс
Проект: Веселый счет 1 класс Раскрытие скобок
Раскрытие скобок Метод парных сравнений
Метод парных сравнений Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать
Презентация по математике "ВЕСЕЛАЯ МАТЕМАТИКА" - скачать  Решение уравнений математической физики методом д’Аламбера
Решение уравнений математической физики методом д’Аламбера Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.
Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.  Методы обработки числовых данных
Методы обработки числовых данных Основные теоремы и формулы планиметрии
Основные теоремы и формулы планиметрии Типы текстовых задач в ЕГЭ
Типы текстовых задач в ЕГЭ Ковариация, дисперсия и корреляция
Ковариация, дисперсия и корреляция Числовые неравенства. Свойства числовых неравенств
Числовые неравенства. Свойства числовых неравенств ПРЕЗЕНТАЦИЯ НА ТЕМУ: «ДЕКАРТОВО ПРОИЗВЕДЕНИЕ» Выполнили: Индюшкина Ольга, Салимова Ксения.
ПРЕЗЕНТАЦИЯ НА ТЕМУ: «ДЕКАРТОВО ПРОИЗВЕДЕНИЕ» Выполнили: Индюшкина Ольга, Салимова Ксения.  ორი სიბრტყის თანაკვეთა
ორი სიბრტყის თანაკვეთა Презентация по математике "Как измерить расстояние между родственниками" - скачать
Презентация по математике "Как измерить расстояние между родственниками" - скачать  Что есть угол? Математика. Лекция №6
Что есть угол? Математика. Лекция №6 Признаки параллельности двух прямых
Признаки параллельности двух прямых Проект выполнил: Денис Панчук, ученик 9 класса МОУ СОШ №2 г.Петровска Научный руководитель: Зинаида Александровна Долгова, препода
Проект выполнил: Денис Панчук, ученик 9 класса МОУ СОШ №2 г.Петровска Научный руководитель: Зинаида Александровна Долгова, препода Системы нелинейных уравнений с двумя неизвестными
Системы нелинейных уравнений с двумя неизвестными Логарифмическая функция
Логарифмическая функция Числовые ряды
Числовые ряды Урок математики, 2 класс «Проверка вычитания»
Урок математики, 2 класс «Проверка вычитания» Регрессионный анализ
Регрессионный анализ Урок математики в 4 классе Учитель: Колупаев Д.В.
Урок математики в 4 классе Учитель: Колупаев Д.В. Биномиальное распределение. Распределение Пуассона
Биномиальное распределение. Распределение Пуассона Готовимся к ЕГЭ. Стереометрия
Готовимся к ЕГЭ. Стереометрия Задания с производной при подготовке к ЕГЭ
Задания с производной при подготовке к ЕГЭ Вычисление объема стволов деревьев
Вычисление объема стволов деревьев Устная работа на уроках математики как средство формирования вычислительных навыков учащихся
Устная работа на уроках математики как средство формирования вычислительных навыков учащихся