14.05.2012
О ПРИМЕНЕНИИ СВОЙСТВ ТРЕУГОЛЬНИКА В ДРЕВНОСТИ.
Греческий мудрец Фалес из Милета
за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался тенью. Как говорит придание , Фалес избрал день и час , когда длинна собственной его тени равнялась его росту , в этот момент высота пирамиды должна также равняться длине отображенной
его тени.
Задача греческого мудреца кажется сейчас нам очень простой , но надо помнить , что было это еще за 300 лет до жизни Евклида , который написал книгу по которой обучаются геометрии до сих пор.
Чтобы измерить высоту пирамиды по ее тени , надо было знать некоторые геометрические свойства треугольника :
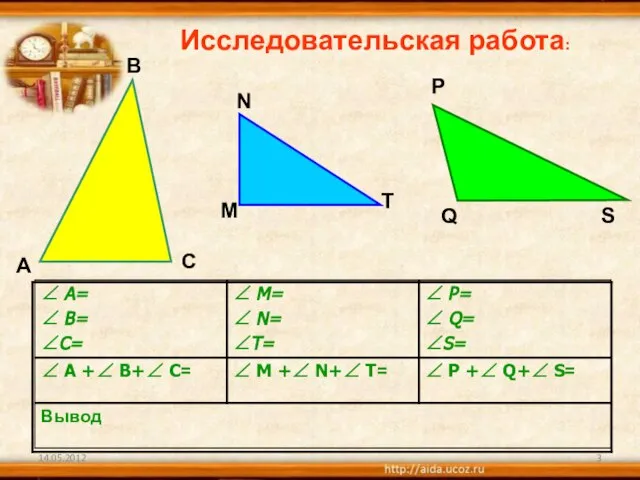
1)что углы при основании равнобедренного треугольника равны , и обратно - что стороны , лежащие против равных углов треугольника, равны между собой.
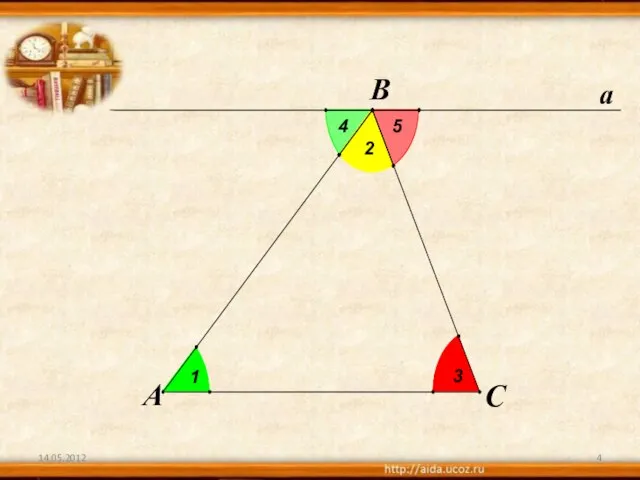
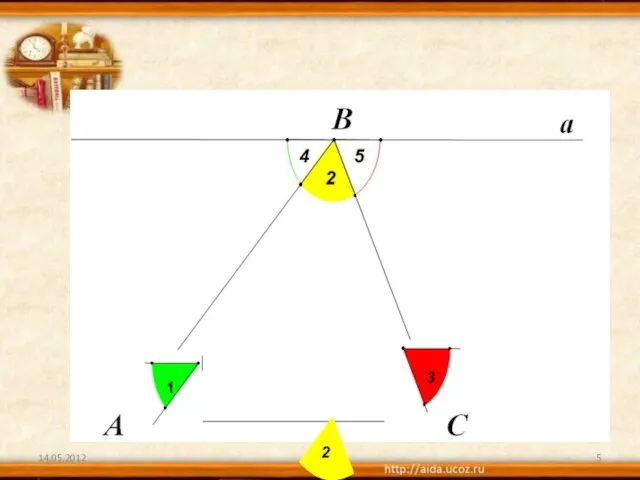
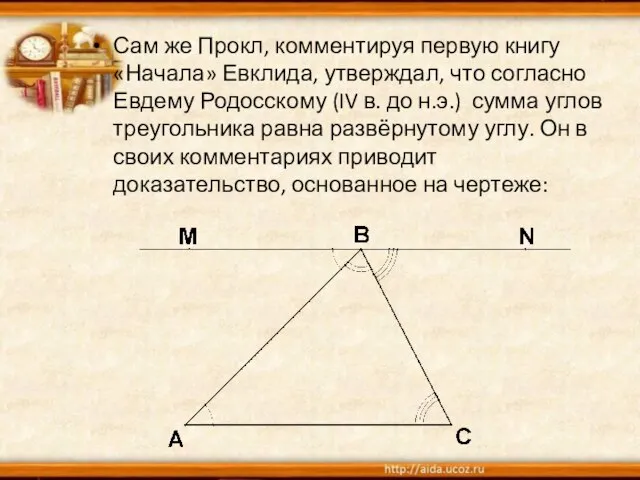
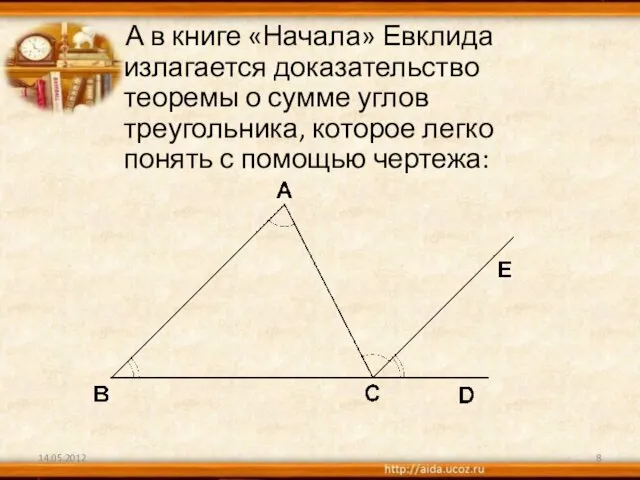
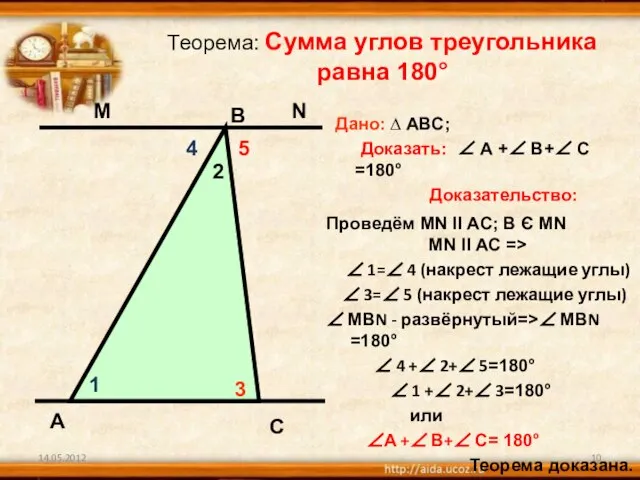
2)Что сумма углов всякого треугольника равна двум прямым углам (180градусов) Только вооруженный этим знанием Фалес вправе был заключить, что когда его собственная тень равна его росту , солнечные лучи встречают ровную почву под углом в половину прямого ,и, следовательно , вершина пирамиды ,центр ее основания и конец ее тени должны обозначить равнобедренный треугольник.
(Конечно , длину тени надо было считать от средней точки квадратного основания пирамиды ; ширину этого основания Фалес мог измерить непосредственно.)







 Числовые ряды
Числовые ряды Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский
Работу выполнила Артамонова Лариса Владимировна - учитель математики первой квалификационной категории, МОУ «Москаленский  Величины: скорость, время и расстояние
Величины: скорость, время и расстояние Учитель начальных классов : Виноградова Нина Николаевна. МБОУ «СОШ № 78», г. Северск, Томской области.
Учитель начальных классов : Виноградова Нина Николаевна. МБОУ «СОШ № 78», г. Северск, Томской области. Применение распределительного свойства умножения
Применение распределительного свойства умножения Решение обыкновенных дифференциальных уравнений (задача Коши)
Решение обыкновенных дифференциальных уравнений (задача Коши) Сумма углов треугольника
Сумма углов треугольника Формулы теории вероятностей
Формулы теории вероятностей Квадратное уравнение и его корни
Квадратное уравнение и его корни Скрещивающиеся прямые
Скрещивающиеся прямые Решение задач с помощью графов
Решение задач с помощью графов Делимость чисел. 5 класс. Мультимедийный, комбинированный урок
Делимость чисел. 5 класс. Мультимедийный, комбинированный урок Решение линейных уравнений. Подготовила учитель математике. Смирнова А.Н.
Решение линейных уравнений. Подготовила учитель математике. Смирнова А.Н. Перпендикуляр к прямой
Перпендикуляр к прямой Плоскость, прямая, луч. 5 класс
Плоскость, прямая, луч. 5 класс Квадратный корень из дроби
Квадратный корень из дроби Формула полной вероятности, испытания Бернулли, Теорема Лапласа, случайные величины. Лекция 2
Формула полной вероятности, испытания Бернулли, Теорема Лапласа, случайные величины. Лекция 2 Подготовка к ЕГЭ. Задачи по геометрии в вариантах ЕГЭ
Подготовка к ЕГЭ. Задачи по геометрии в вариантах ЕГЭ Презентация по математике "Контрольные работы" - скачать
Презентация по математике "Контрольные работы" - скачать  График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Проце́нт. Происхождение процентов
Проце́нт. Происхождение процентов Статистические способы обработки экспериментальных данных
Статистические способы обработки экспериментальных данных Аксиомы, теоремы и методика их изучения в курсе математики средней школы
Аксиомы, теоремы и методика их изучения в курсе математики средней школы Действия с обыкновенными дробями Урок обобщения и систематизации знаний
Действия с обыкновенными дробями Урок обобщения и систематизации знаний  Распределительное свойства умножения
Распределительное свойства умножения Аттестационная работа. Образовательная программа факультативного курса Занимательная математика
Аттестационная работа. Образовательная программа факультативного курса Занимательная математика Тренажёр таблицы умножения
Тренажёр таблицы умножения Аттестационная работа. Методическая разработка по выполнению проектной работы Паркеты, бордюры, орнаменты
Аттестационная работа. Методическая разработка по выполнению проектной работы Паркеты, бордюры, орнаменты