Введение в комбинаторику

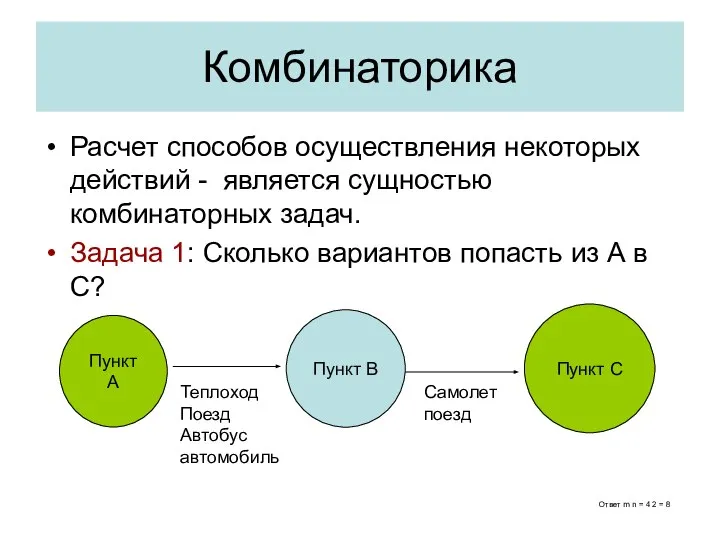
Комбинаторика

Расчет способов осуществления некоторых действий - является сущностью комбинаторных задач.
Задача 1:

Введение

ЗАДАЧА 2: В соревновании участвуют 16 команд. Сколько способов распределения золотой,

Основное правило комбинаторики

Правило умножения.
Если необходимо выполнить по порядку k действий. Первое

Задача

Задача 3. Сколько четырех значных чисел можно составить из цифр {1,2,3,4,5},

Задача

Задача 4. На гору ведет 7 дорог. Сколько вариантов подняться и

Вычисление числа элементов суммы множеств

Если задано множество А и множество В,

Задача 5

Задача 5. Каждый студент группы либо девушка, либо имеет светлые

Решение задачи 5

Пусть А множество студенток – 20.
В –

Ответ задачи 5

Подставляем числа в формулу вычисления суммы числа трех множеств:

Теорема о числе элементов объединения множеств

Если А1,…,Аn – некоторые множества, то

Продолжение теоремы

Правая часть этого равенства является суммой n слагаемых, где к

Упорядоченное множество

Определение: множество из которого задан порядок его элементов называется упорядоченным.

Число возможных слов длины k из алфавита мощностью n

Пусть задано два

Принцип математической индукции

Пусть имеется конечное упорядоченное множество n натуральных чисел А

Принцип математической индукции

1) Если некоторое утверждение справедливо для k=1.
2) из справедливости

Пример доказательства

При n = 1 неравенство выполняется.
Предположим, что выполняется неравенство
Докажем, что

Понятие собственного подмножества

Если каждый элемент множества В принадлежит множеству А, то

Множество всех его подмножеств

Если задано множество А, то можно рассматривать новое

Пример множества всех подмножеств

Пусть А={a,b,c}, тогда
М(А)={{a},{b},{c},{a,b},{a,с},{b,с},{a,b,c}, }
{{a,b},{a,с},{b,с}}

ВОПРОС –

Число сочетаний из n по k

ТЕОРЕМА: Число всех k - элементарных

Примеры задач

Задача 6. Сколько способов выбора трех книг из пяти.
Задача 7.

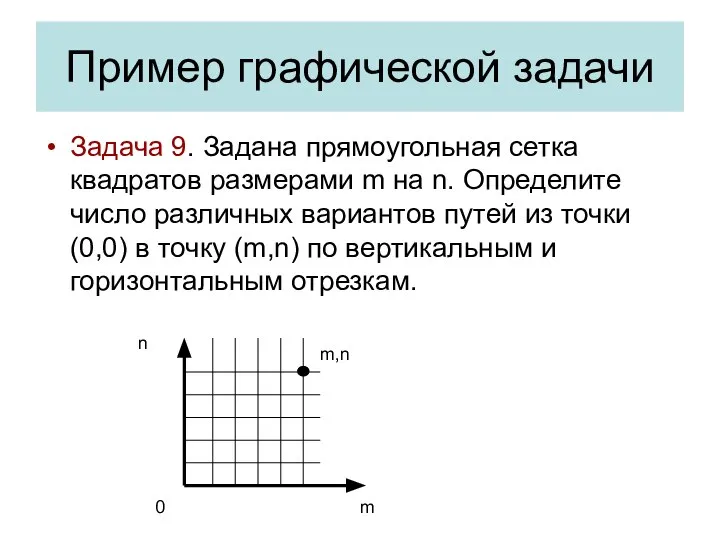
Пример графической задачи

Задача 9. Задана прямоугольная сетка квадратов размерами m на

Теорема о сумме числа сочетаний

Число сочетаний из n по k равно

Теорема о сумме числа сочетаний

ДОКАЗАТЕЛЬСТВО:
Число кратчайших путей из точки (0,0) в

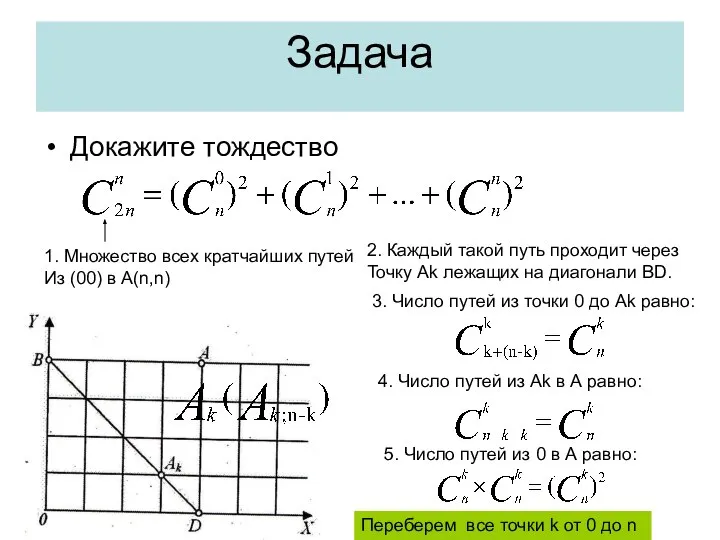
Задача

Докажите тождество

1. Множество всех кратчайших путей
Из (00) в А(n,n)

2. Каждый такой

Количество подмножеств данного множества

ВОПРОС. Сколько всего подмножеств имеет множество А, состоящее

Следствие теоремы

Имеет место равенство:

Действительно, если число k – элементных подмножеств множества

Упорядоченные множества. Перестановки и размещения

Множество называется упорядоченным. Если каждому элементу множества

Варианты перестановок множества

Пусть задано множество А из n – элементов, а

Примеры

Задача 11. Сколькими способами можно поставить 4 книги на полке.
Задача 12.

Число размещений длины k из алфавита n

Число размещений длины k из