Содержание
- 2. Зміст Вступ…………………………………………………. 3 Шлях…………………….………………………….. 4 Цикл.................................... …………………………..6 Теорема............................................................... ……..7 Орієнтований граф …………………………………..8 Зв’язаність графів................................ ……………….9 Ізоморфізм
- 3. Вступ Теорія графів — одна з істотних частин математичного апарату інформатики та кібернетики. У термінах теорії
- 4. Шлях Шляхом довжиною r [52] із вершини и в вершину v в неорієнтованому графі називають послідовність
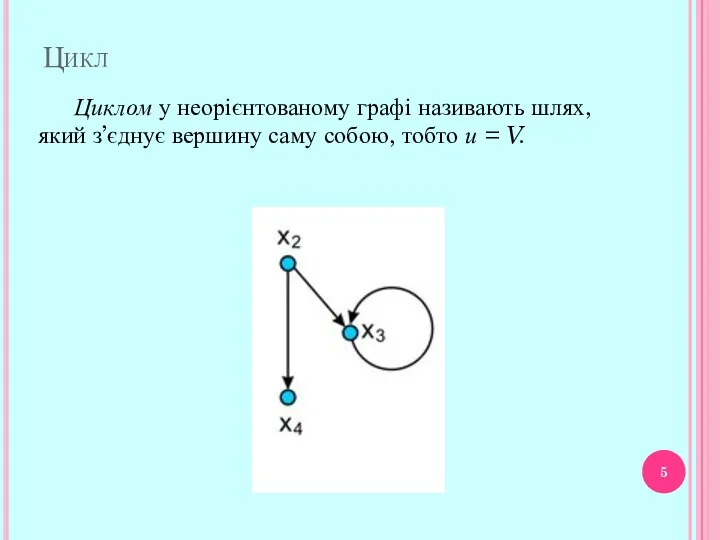
- 5. Циклом у неорієнтованому графі називають шлях, який з’єднує вершину саму собою, тобто и = V. Цикл
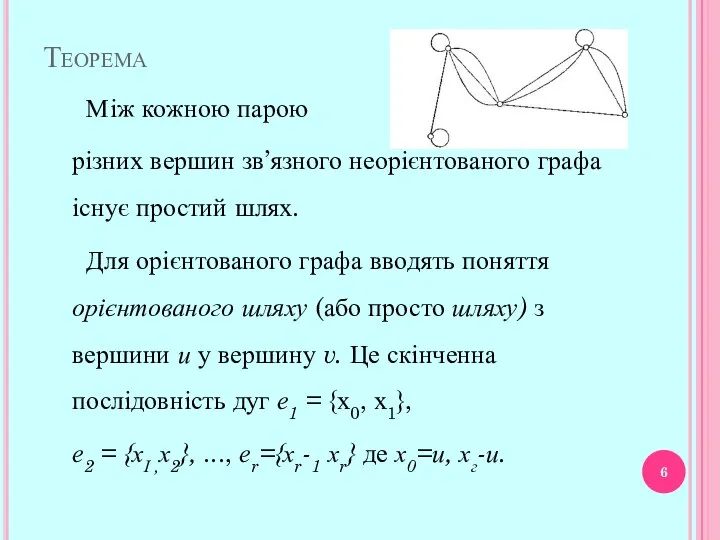
- 6. Теорема Між кожною парою різних вершин зв’язного неорієнтованого графа існує простий шлях. Для орієнтованого графа вводять
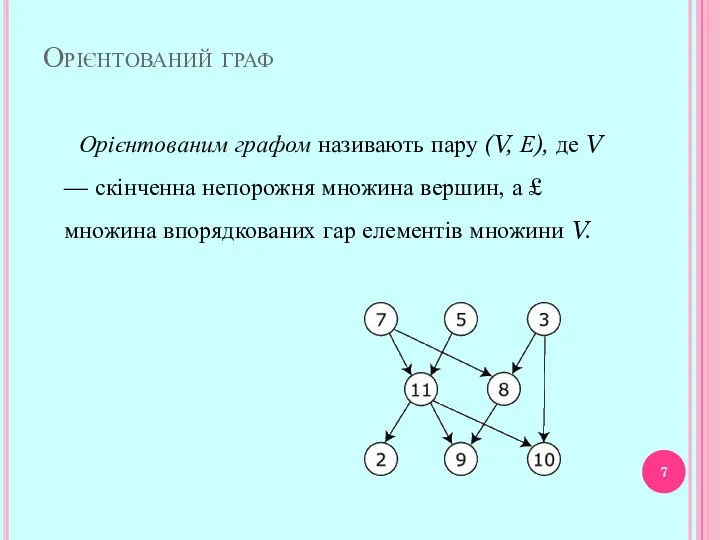
- 7. Орієнтований граф Орієнтованим графом називають пару (V, Е), де V — скінченна непорожня множина вершин, а
- 8. Зв’язаність графів Орієнтований граф називають сильно зв’язним, якщо для будь-яких його різних вершин и та V
- 9. Ізоморфізм графів У теорії графів і її застосуваннях істотно, що існують об’єкти (вершини графа) і зв’язки
- 10. Нехай G1 = (VІ, Е1) і G2=(V2, Е2) прості графи, а φ: Vх → V2 —
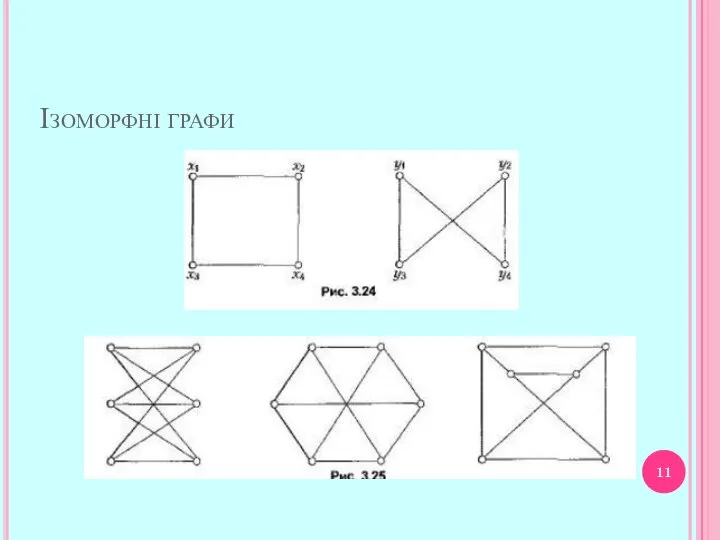
- 11. Ізоморфні графи
- 12. Теорема Прості графи ізоморфні тоді й лише тоді, коли їх матриці суміжності можна отримати одну з
- 13. Проблема визначення Часто неважко довести, що два прості графи не ізоморфні, якщо порушується ачастивість, інваріантна щодо
- 14. Висновки Отже, не існує набору інваріантів для виявлення ізоморфізму. Для сильної зв’язності орієнтованого графа має існувати
- 16. Скачать презентацию


![Шлях Шляхом довжиною r [52] із вершини и в вершину v](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1464855/slide-3.jpg)






 Решение матричных игр в смешанных стратегиях 2xn и mx2
Решение матричных игр в смешанных стратегиях 2xn и mx2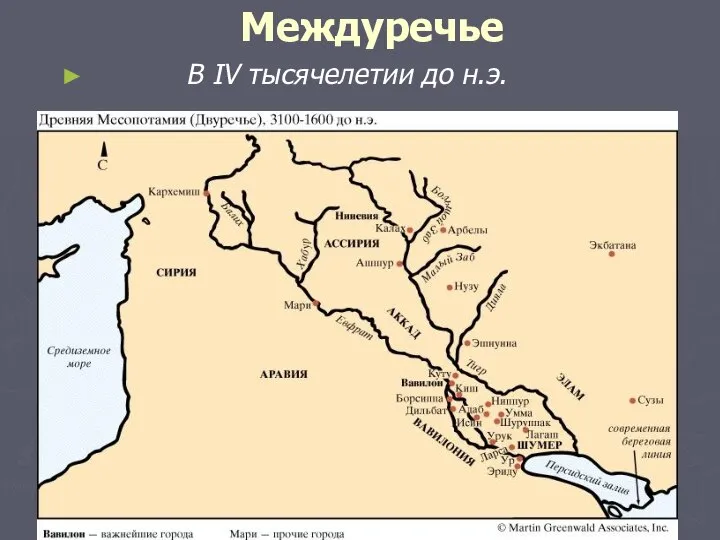 Междуречье В IV тысячелетии до н.э.
Междуречье В IV тысячелетии до н.э. Задачи на проценты
Задачи на проценты Фестиваль педагогических идей «Открытый урок» Конкурс «Презентация к уроку» Тема: Геометрические фигуры. 5 класс
Фестиваль педагогических идей «Открытый урок» Конкурс «Презентация к уроку» Тема: Геометрические фигуры. 5 класс  Сравнение дробей
Сравнение дробей Сложные суждения. (Тема 4)
Сложные суждения. (Тема 4) Признаки равенства треугольников
Признаки равенства треугольников Состав чисел от 2 до 10
Состав чисел от 2 до 10 Деление с остатком
Деление с остатком Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1)
Анализ вариационных рядов. Предмет и задачи математической статистики. (Глава 1.1) Приёмы устных вычислений (урок 116)
Приёмы устных вычислений (урок 116) Применение распределительного свойства умножения. 6 класс
Применение распределительного свойства умножения. 6 класс Перестановки и размещения
Перестановки и размещения Пропорція. Основна властивість пропорції
Пропорція. Основна властивість пропорції Непрерывность функции одной переменной
Непрерывность функции одной переменной Многогранники. Правильные многогранники
Многогранники. Правильные многогранники Геометрический смысл двойного интеграла
Геометрический смысл двойного интеграла Квадратурные формулы Ньютона-Котеса
Квадратурные формулы Ньютона-Котеса Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса
Оптимизация тематического моделирования за счет изменения функции плотности в алгоритме семплирования Гиббса Цилиндр, конус, шар
Цилиндр, конус, шар Model Parameterization in tomography problems. Lecture 4
Model Parameterization in tomography problems. Lecture 4 Конус
Конус Однофакторні нелінійні економетричні моделі
Однофакторні нелінійні економетричні моделі последовательности и Династия Романовых
последовательности и Династия Романовых  Функция распределения случайной величины
Функция распределения случайной величины Признаки параллельности прямых
Признаки параллельности прямых Симметрия вокруг нас
Симметрия вокруг нас