Содержание
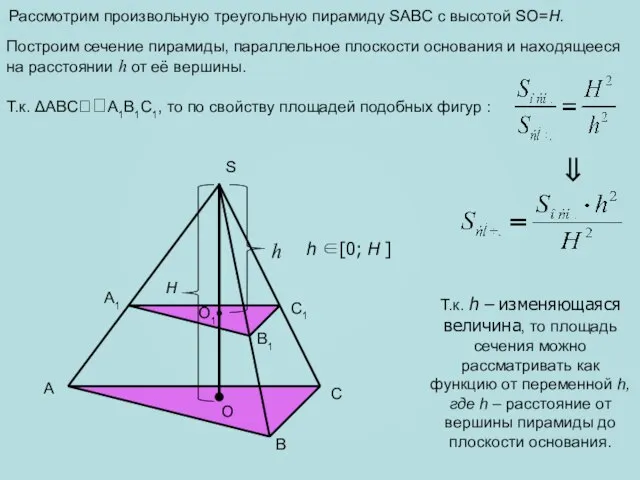
- 2. Рассмотрим произвольную треугольную пирамиду SABC с высотой SO=H. A B C S O H O1 h
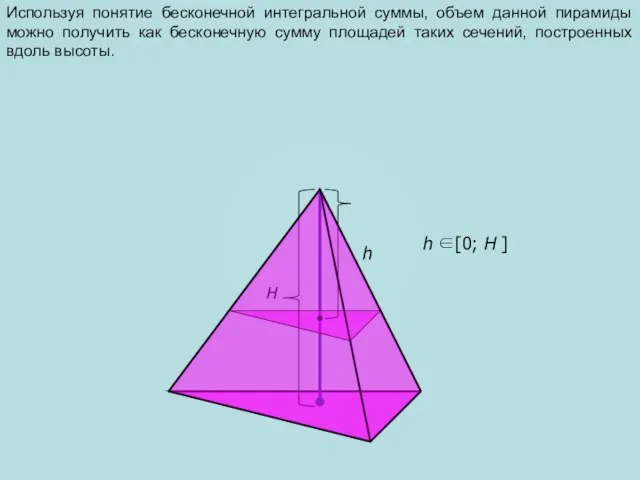
- 3. h H Используя понятие бесконечной интегральной суммы, объем данной пирамиды можно получить как бесконечную сумму площадей
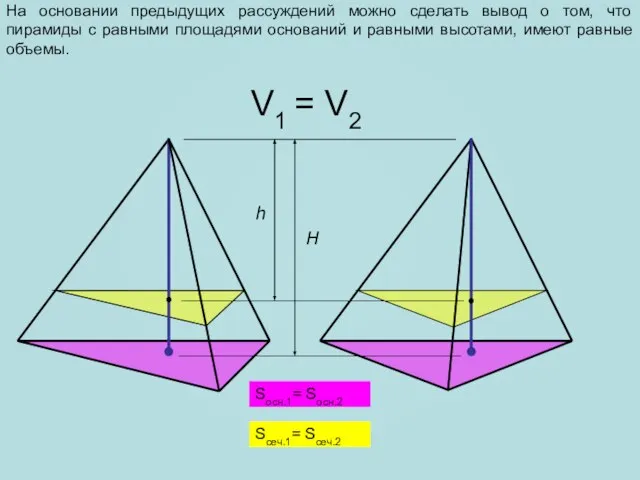
- 4. На основании предыдущих рассуждений можно сделать вывод о том, что пирамиды с равными площадями оснований и
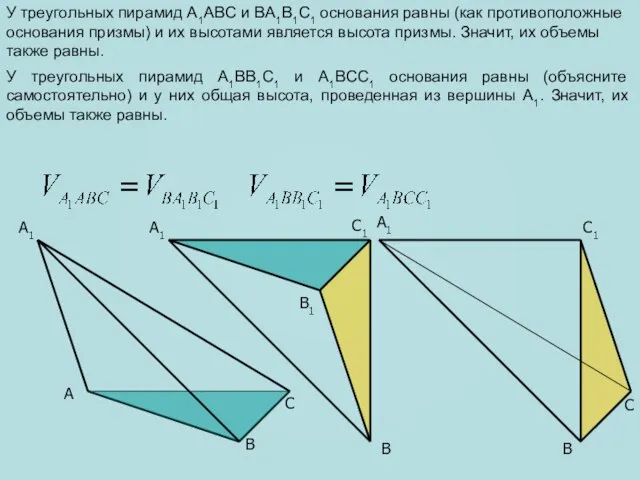
- 5. A B C B1 A1 C1 C A1 B Рассмотрим произвольную треугольную призму ABCA1B1C1. Разобьем её
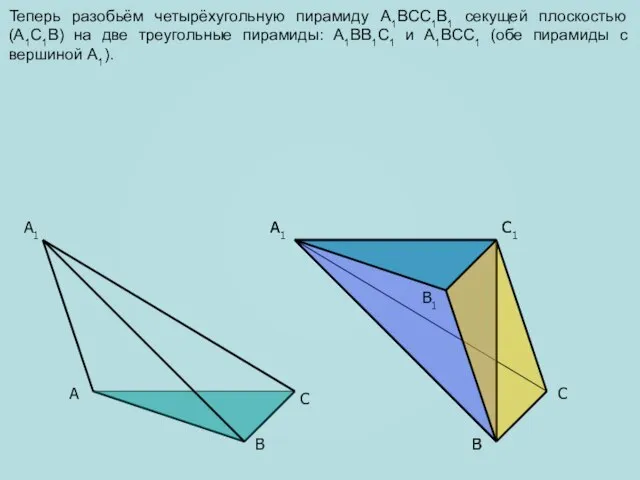
- 6. A C B1 A1 C1 C A1 B B Теперь разобьём четырёхугольную пирамиду A1BCC1B1 секущей плоскостью
- 7. A C B1 A1 C1 C A1 B B A1 C1 B У треугольных пирамид A1ABC
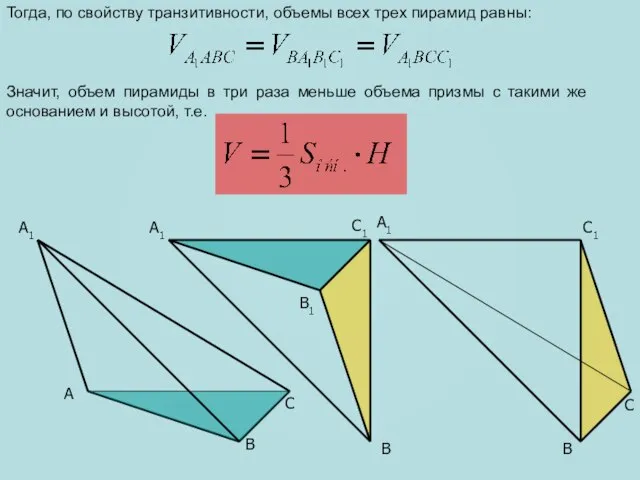
- 8. A C B1 A1 C1 C A1 B B A1 C1 B Тогда, по свойству транзитивности,
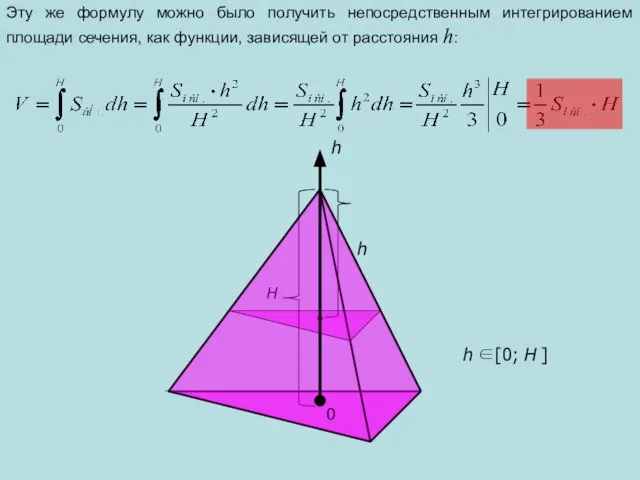
- 9. h H h Эту же формулу можно было получить непосредственным интегрированием площади сечения, как функции, зависящей
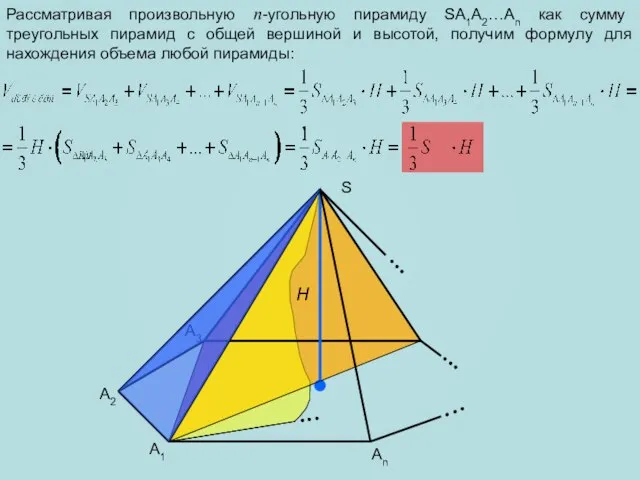
- 10. Рассматривая произвольную n-угольную пирамиду SA1A2…An как сумму треугольных пирамид с общей вершиной и высотой, получим формулу
- 12. Скачать презентацию

 Исследование окружности - презентация по Геометрии_
Исследование окружности - презентация по Геометрии_ Комбинации шара (сферы) с многогранниками и фигурами вращения. Геометрия, 11 класс.
Комбинации шара (сферы) с многогранниками и фигурами вращения. Геометрия, 11 класс. Центральные углы и углы, вписанные в окружность Латыпова С.В. МОУ СОШ № 83 г. Ярославль
Центральные углы и углы, вписанные в окружность Латыпова С.В. МОУ СОШ № 83 г. Ярославль  ПРЕДМЕТ ЧЕРЧЕНИЕ И ЕГО РОЛЬ В ОБЩЕСТВЕ ВВОДНЫЙ УРОК. 8кл.
ПРЕДМЕТ ЧЕРЧЕНИЕ И ЕГО РОЛЬ В ОБЩЕСТВЕ ВВОДНЫЙ УРОК. 8кл. Третий признак равенства треугольников
Третий признак равенства треугольников Две плоскости, cодержащие прямую DE - презентация по Геометрии_
Две плоскости, cодержащие прямую DE - презентация по Геометрии_ Вычисление объёма фигур - презентация по Геометрии_
Вычисление объёма фигур - презентация по Геометрии_ Симметрия Урок математики в 4-а классе Учитель: Барабанова Галина Александровна
Симметрия Урок математики в 4-а классе Учитель: Барабанова Галина Александровна  Решение задач по теме Цилиндр - презентация по Геометрии
Решение задач по теме Цилиндр - презентация по Геометрии Хроника развития тригонометрии.
Хроника развития тригонометрии.  Исследование графика функции с помощью производной. Учитель ЯГЛ Крючкова Е.А. 2014г.
Исследование графика функции с помощью производной. Учитель ЯГЛ Крючкова Е.А. 2014г. Первый признак равенства треугольников Геометрия 7 класс
Первый признак равенства треугольников Геометрия 7 класс  Объёмы геометрических тел - презентация по Геометрии
Объёмы геометрических тел - презентация по Геометрии Тема урока: Компланарные векторы. Правило параллелепипеда.
Тема урока: Компланарные векторы. Правило параллелепипеда. Шар и сфера. Урок 1.
Шар и сфера. Урок 1. Правильные многогранники Презентацию подготовила Шевцова Маргарита, СО-ТВ-13
Правильные многогранники Презентацию подготовила Шевцова Маргарита, СО-ТВ-13 Математика в медицине. Миф или реальность?
Математика в медицине. Миф или реальность?  Соотношения между сторонами и углами треугольника - презентация по Геометрии
Соотношения между сторонами и углами треугольника - презентация по Геометрии Окружность и круг методическая разработка Выполнила учитель математики МОУ «Лицей-интернат им. Г.С.Лебедева г.Чебоксары» Селянк
Окружность и круг методическая разработка Выполнила учитель математики МОУ «Лицей-интернат им. Г.С.Лебедева г.Чебоксары» Селянк Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Центральная симметрия.
Центральная симметрия. «Точка, прямая, отрезок, луч и угол»
«Точка, прямая, отрезок, луч и угол»  Соотношения между сторонами и углами в прямоугольном треугольнике - презентация по Геометрии____________________________________________________________________
Соотношения между сторонами и углами в прямоугольном треугольнике - презентация по Геометрии____________________________________________________________________ Различные способы доказательства теоремы Пифагора По материалам Интернета исследование провела учитель математики МКОУ Бук
Различные способы доказательства теоремы Пифагора По материалам Интернета исследование провела учитель математики МКОУ Бук Треугольник - презентация по Геометрии_
Треугольник - презентация по Геометрии_ Первый признак равенства треугольников Выполнила: учитель математики Римпинская Нина Ивановна МБОУ СОШ№2 г. Лангепас
Первый признак равенства треугольников Выполнила: учитель математики Римпинская Нина Ивановна МБОУ СОШ№2 г. Лангепас Симметрия вокруг нас - презентация по Геометрии
Симметрия вокруг нас - презентация по Геометрии Виды соединения деталей Выполнил : Кандыба Игорь Ученик 9а класса МОУ СОШ №40
Виды соединения деталей Выполнил : Кандыба Игорь Ученик 9а класса МОУ СОШ №40