Содержание
- 2. Линейные уравнения с постоянными коэффициентами Однородные Д.У. с постоянными коэффициентами. Рассмотрим уравнение где - постоянные действительные
- 3. Линейные уравнения с постоянными коэффициентами Определение. Алгебраическое уравнение соответствующее данному ЛОДУ, называется характеристическим уравнением. Обратное утверждение:
- 4. Линейные уравнения с постоянными коэффициентами Примеры. 1. Замена: Характеристическое уравнение: - частные решения ЛОДУ.
- 5. Линейные уравнения с постоянными коэффициентами Примеры. 2. Замена: Характеристическое уравнение: - частные решения ЛОДУ.
- 6. Линейные уравнения с постоянными коэффициентами Свойства решений ЛОДУ. 1. Линейность. - решения ЛОДУ - решение ЛОДУ.
- 7. Линейные уравнения с постоянными коэффициентами Свойства решений ЛОДУ. 1. Линейность. - решения ЛОДУ - решение ЛОДУ.
- 8. Линейные уравнения с постоянными коэффициентами 2. Критерий линейной независимости системы решений ЛОДУ. Пусть - частные решения
- 9. Линейные уравнения с постоянными коэффициентами Определение ФСР. Фундаментальной системой решений (ФСР) ЛОДУ - порядка n называется
- 10. Линейные уравнения с постоянными коэффициентами Определение ФСР. Фундаментальной системой решений (ФСР) ЛОДУ - порядка n называется
- 11. Линейные уравнения с постоянными коэффициентами Теорема о структуре общего решения ЛОДУ. Пусть при система образует ФСР
- 12. Линейные уравнения с постоянными коэффициентами ФСР в случае различных действительных корней. Доказательство (при n=2). 1. 2.
- 13. Линейные уравнения с постоянными коэффициентами Случай кратных действительных корней. Пусть действительное число - корень уравнения кратности
- 14. Линейные уравнения с постоянными коэффициентами Случай кратных действительных корней. Пусть действительное число - корень уравнения кратности
- 15. Линейные уравнения с постоянными коэффициентами ФСР в случае, когда некоторые корни комплексные. 1. Случай простого комплексного
- 16. Линейные уравнения с постоянными коэффициентами Преобразуем функции с помощью формулы Эйлера: Функции являются действительными функциями переменной
- 17. Линейные уравнения с постоянными коэффициентами Примеры. 1. Найти ФСР уравнения Шаг 1. Запишем характеристическое уравнение и
- 18. Линейные уравнения с постоянными коэффициентами Примеры. 2. Найти ФСР уравнения Шаг 1. Запишем характеристическое уравнение и
- 19. Линейные уравнения с постоянными коэффициентами 2. Случай кратных комплексных корней. Пусть комплексное число корень кратности число
- 20. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения с постоянными коэффициентами. Свойства решений ЛНДУ. . 1. -
- 21. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения с постоянными коэффициентами. Свойства решений ЛНДУ. . 1. -
- 22. Линейные уравнения с постоянными коэффициентами 2. Принцип суперпозиции.
- 23. Линейные уравнения с постоянными коэффициентами 2. Принцип суперпозиции. Доказательство.
- 24. Линейные уравнения с постоянными коэффициентами Теорема о структуре общего решения ЛНДУ. 1. - частное решение ЛНДУ
- 25. Линейные уравнения с постоянными коэффициентами Неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов. Рассмотрим уравнение где
- 26. Линейные уравнения с постоянными коэффициентами Примеры. 1. Найти общее решение уравнения Шаг 1. Решим ЛОДУ, соответствующее
- 27. Линейные уравнения с постоянными коэффициентами 2. Найти общее решение ЛНДУ Шаг 1. Решим ЛОДУ, соответствующее данному
- 28. Линейные уравнения с постоянными коэффициентами Пример 3. Найти общее решение ЛНДУ Шаг 1. Решим ЛОДУ, соответствующее
- 29. Линейные уравнения с постоянными коэффициентами Пример 4. Найти общее решение ЛНДУ Шаг 1. Решим ЛОДУ, соответствующее
- 30. Линейные уравнения с постоянными коэффициентами Линейные неоднородные Д.У. Метод вариации произвольных постоянных (метод Лагранжа). Теорема. -
- 31. Линейные уравнения с постоянными коэффициентами Частный случай. Рассмотрим ЛНДУ второго порядка Пусть - ФСР соответствующего ЛОДУ
- 32. Линейные уравнения с постоянными коэффициентами Пример. Решение. 1. ЛОДУ ФСР 2. Общее решение ЛОДУ 3. Частное
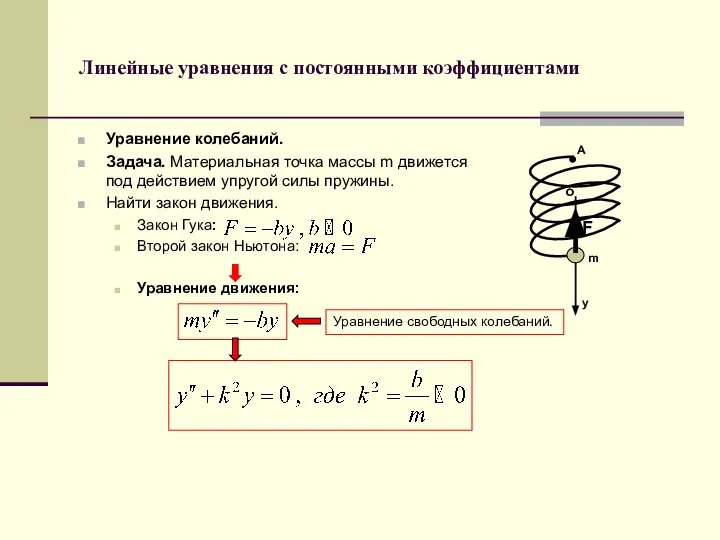
- 33. Линейные уравнения с постоянными коэффициентами Уравнение колебаний. Задача. Материальная точка массы m движется под действием упругой
- 34. Линейные уравнения с постоянными коэффициентами Характеристическое уравнение: ФСР: Общее решение: Задача Коши. Свободные колебания с амплитудой
- 36. Скачать презентацию
































 Интервальное оценивание
Интервальное оценивание Четырехугольники. Его компоненты и свойства
Четырехугольники. Его компоненты и свойства Взаимное расположение сферы и плоскости
Взаимное расположение сферы и плоскости Палички Непера
Палички Непера Геометрический метод решения задачи линейного программирования
Геометрический метод решения задачи линейного программирования Линейные неравенства с одним неизвестным
Линейные неравенства с одним неизвестным Методы решения уравнений
Методы решения уравнений Зарождение алгебры
Зарождение алгебры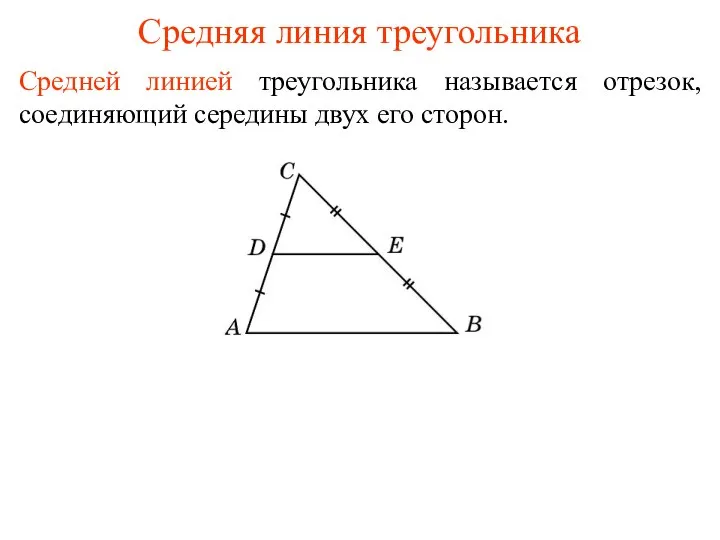 Средняя линия треугольника
Средняя линия треугольника Решение систем линейных алгебраических уравнений
Решение систем линейных алгебраических уравнений Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Теория вероятностей. Случайные величины
Теория вероятностей. Случайные величины Рациональ саннар белән гамәлләр башкару
Рациональ саннар белән гамәлләр башкару Множество и его элементы
Множество и его элементы Центральные и вписанные углы
Центральные и вписанные углы Призма
Призма Преобразование графиков функции
Преобразование графиков функции Функцияны туынды арқылы зерттеу
Функцияны туынды арқылы зерттеу Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Признаки равенства треугольников
Признаки равенства треугольников Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.
Сравнение, сложение и вычитание дробей с разными знаменателями и смешанных чисел.  Математика и искусство
Математика и искусство Деление с остатком
Деление с остатком 5 класс
5 класс  Интернет ресурсы при подготовке к ГИА по математике
Интернет ресурсы при подготовке к ГИА по математике Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать бесплатно
Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать бесплатно Вычитание
Вычитание Числовые последовательности. 9 класс
Числовые последовательности. 9 класс