Содержание
- 2. Кто ввел понятие о формулах сокращенного умножения? Формулы сокращённого умножения многочленов — часто встречающиеся случаи умножения
- 3. Однако историки науки обнаружили, что формула была известна ещё китайскому математику Яну Хуэю, жившему в XIII
- 4. Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все
- 5. Формулы сокращенного умножения для квадратов:
- 6. Формулы сокращенного умножения для кубов:
- 7. Формулы сокращенного умножения для четвертой степени:
- 8. Формулы сокращенного умножения для n-ой степени:
- 9. Задачи 1.Представить в виде многочлена
- 10. Применяем формулу квадрата разности и получаем:
- 11. 2. Представить в виде многочлена :
- 12. Очевидно, что можно решить задачу открыв первые две скобки, далее последующие две. Но, если присмотреться, можно
- 13. 3.Подставить вместо многоточия одночлены так, чтобы выполнялось равенство:
- 14. Согласно формуле сокращенного умножения квадрата разницы найдем второй член в равенстве слева. Его квадрат равен 50y,
- 16. 4. Преобразуйте в многочлен выражение:
- 18. Список литературы: 1.Википедия 2.”Только факты” под редакцией Ридерс Дайджест. 3. www.Grandars.ru
- 20. Скачать презентацию













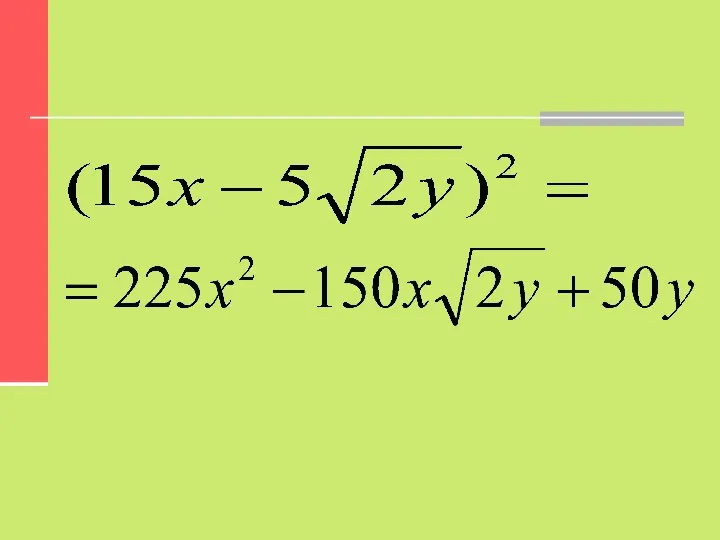

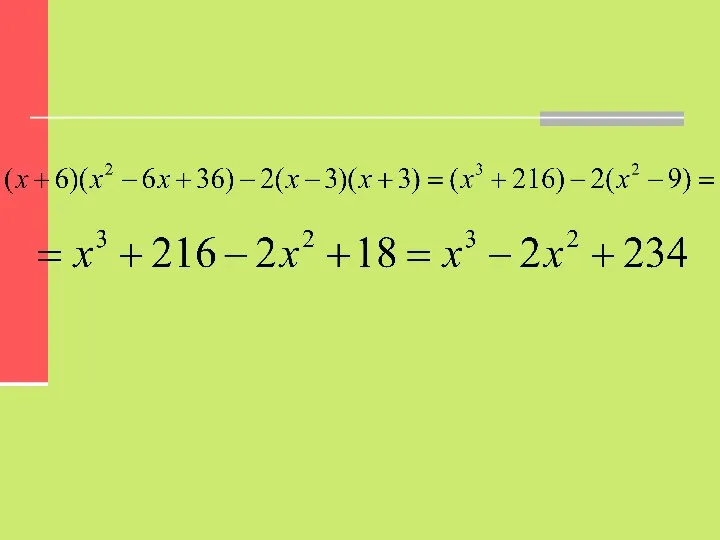

 Системи лінійних алгебраїчних рівнянь
Системи лінійних алгебраїчних рівнянь Тестовые задания для ЕНТ - 2017
Тестовые задания для ЕНТ - 2017 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности ОГЭ по математике – 2018 год
ОГЭ по математике – 2018 год Множества. Операции над множествами
Множества. Операции над множествами Повторяем дроби
Повторяем дроби Математический бой. Внеклассное мероприятие по математике
Математический бой. Внеклассное мероприятие по математике Дифференциальные уравнения 2-го порядка Лекция 5
Дифференциальные уравнения 2-го порядка Лекция 5 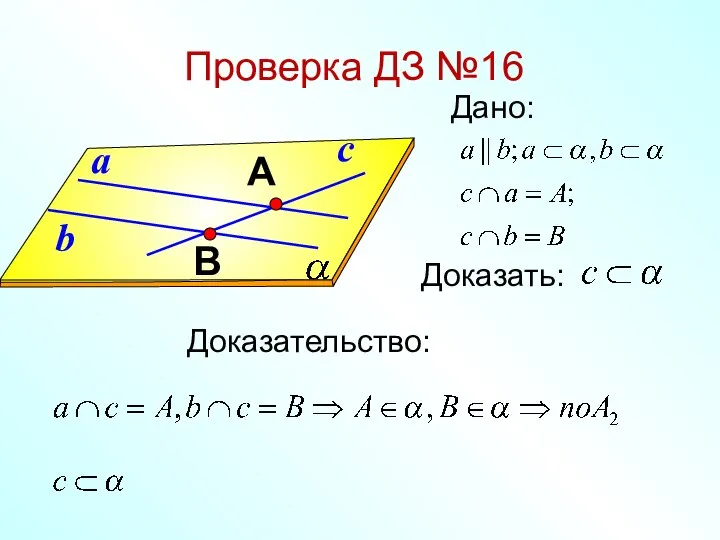 Параллельность прямой и плоскости
Параллельность прямой и плоскости Координатная плоскость
Координатная плоскость Алгебраические методы решения геометрических задач
Алгебраические методы решения геометрических задач Аксиома параллельных прямых
Аксиома параллельных прямых Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды
Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды Пираты Карибского моря. Математика
Пираты Карибского моря. Математика Комплексные числа
Комплексные числа Порядок выполнения действий
Порядок выполнения действий Теорема умножения вероятностей. Решение задач В-10
Теорема умножения вероятностей. Решение задач В-10 Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать
Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать  Геометрические тела
Геометрические тела Аттестационная работа. Создание творческого проекта «Задачи на движение»
Аттестационная работа. Создание творческого проекта «Задачи на движение» Элементы векторной алгебры (лекция № 2)
Элементы векторной алгебры (лекция № 2) Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов)
Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов) Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.
Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.  Математическая сказка «Гуси-лебеди»
Математическая сказка «Гуси-лебеди» Смежные углы
Смежные углы Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан
Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан Правильные многогранники
Правильные многогранники Методы многопарметрической оптимизации
Методы многопарметрической оптимизации