Содержание
- 2. Понятие о совместной функции распределения случайных величин Определения: Функция нескольких переменных: где – х1, х2,…, хn
- 3. Функция распределения случайной величины ξ : при каждом равная вероятности случайной величине ξ принимать значения, меньшие
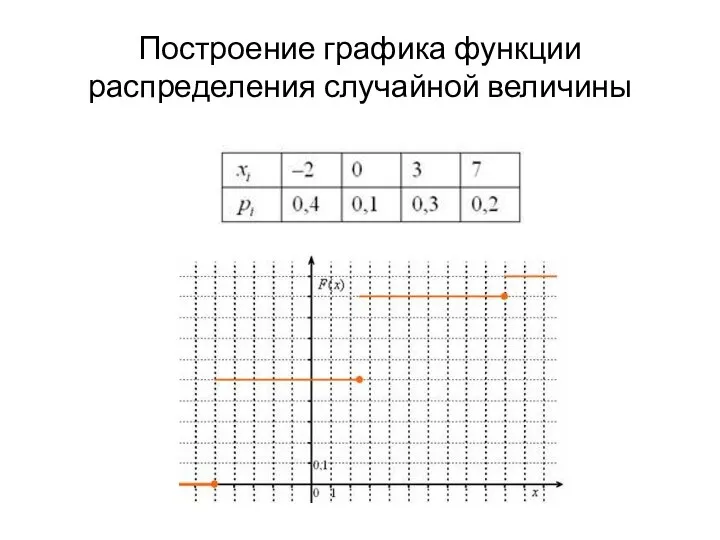
- 4. Построение графика функции распределения случайной величины
- 5. Функция совместного распределения случайных величин: Функция называется функцией распределения вектора или функцией совместного распределения случайных величин
- 6. Свойства функции совместного распределения Свойство 1: Функция распределения F (x,y) есть неубывающая функция обоих своих аргументов,
- 7. Свойства функции совместного распределения Свойство 2: Повсюду на -ꝏ функция распределения равна нулю: F(х, -ꝏ) =
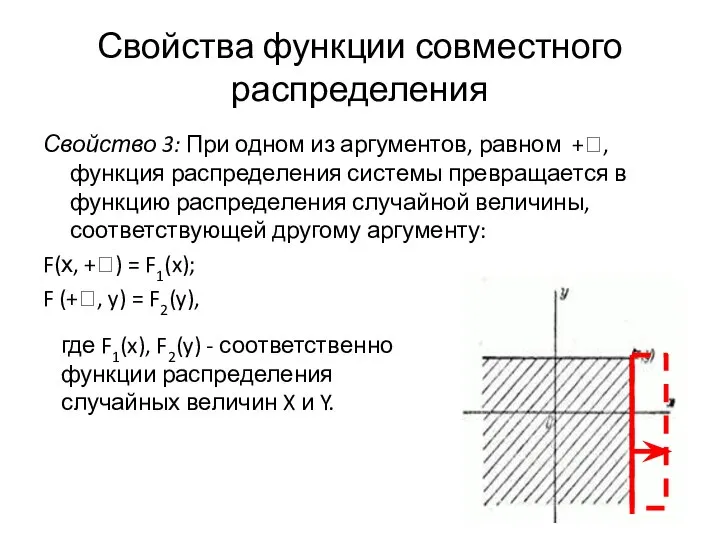
- 8. Свойство 3: При одном из аргументов, равном +ꝏ, функция распределения системы превращается в функцию распределения случайной
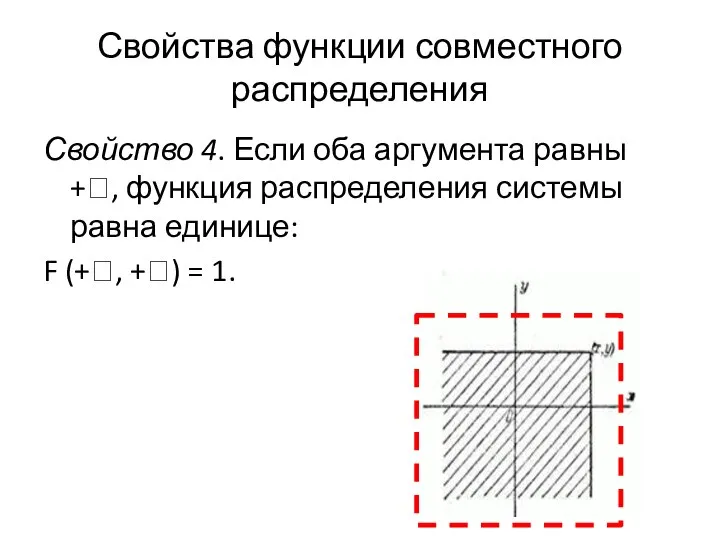
- 9. Свойство 4. Если оба аргумента равны +ꝏ, функция распределения системы равна единице: F (+ꝏ, +ꝏ) =
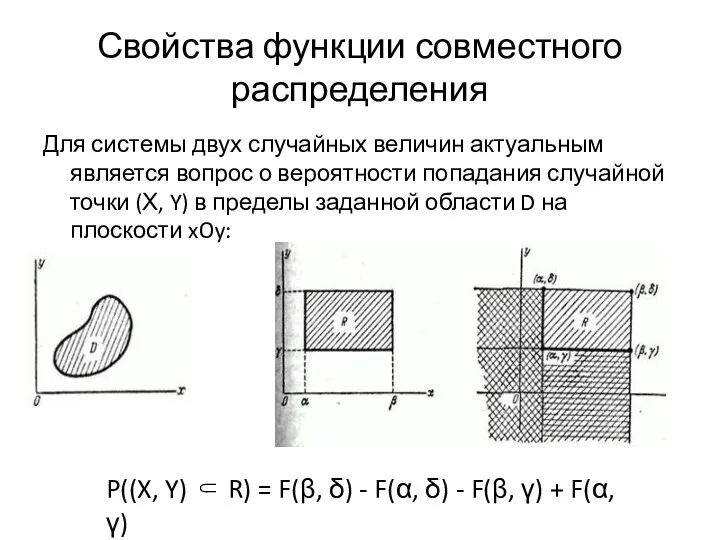
- 10. Для системы двух случайных величин актуальным является вопрос о вероятности попадания случайной точки (Х, Y) в
- 11. Доверительные интервалы для параметра а в случае выборки из нормального распределения N (а,σ2): а) при известном
- 12. Определения: Генеральная совокупность - совокупность всех объектов (единиц), относительно которых предполагается делать выводы при изучении конкретной
- 13. Функция распределения случайной величины Х - Математическое ожидание - мера среднего значения случайной величины в теории
- 14. Закон распределения – это некоторая функция, полностью описывающая случайную величину с вероятностной точки зрения. Нормальное распределение
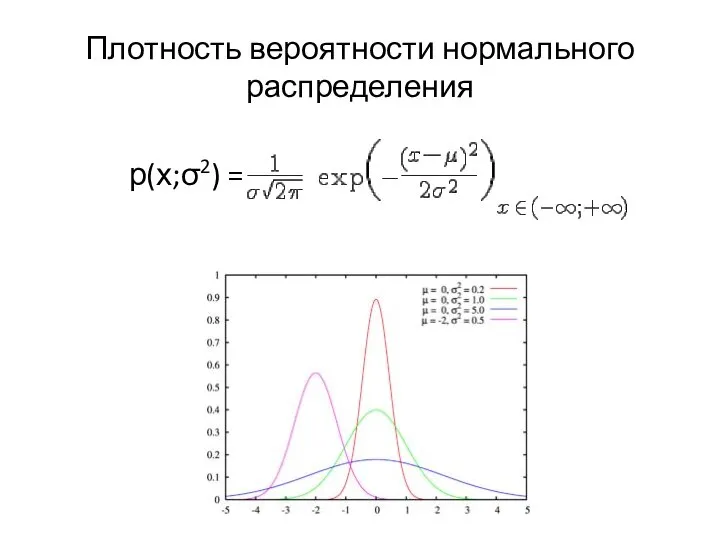
- 15. Плотность вероятности нормального распределения
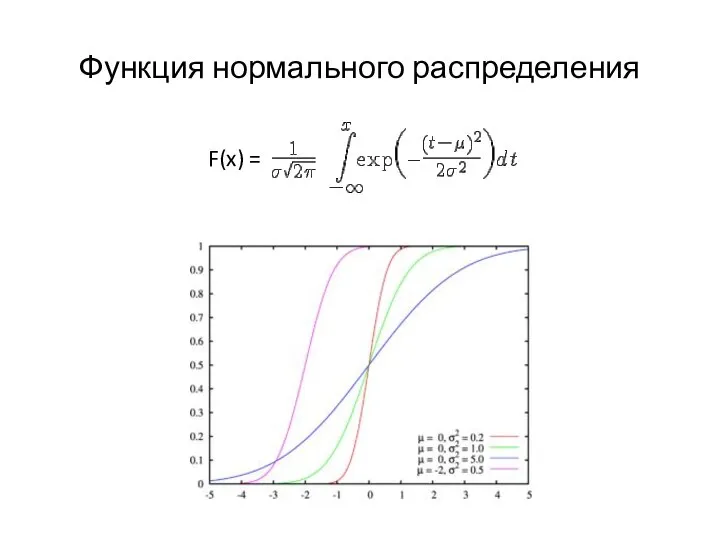
- 16. Функция нормального распределения
- 17. Доверительный интервал - это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой,
- 18. Зафиксируем близкое к нулю положительное число α (например, 0.05 или 0.01). Пусть α = α1+ α2.
- 19. Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и известной дисперсии
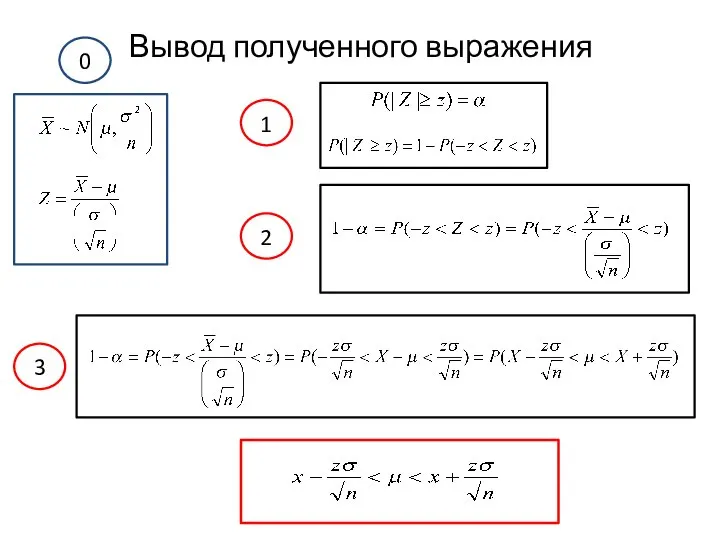
- 20. Вывод полученного выражения
- 21. Доверительный интервал для математического ожидания (μ) в случае нормальной генеральной совокупности и неизвестной дисперсии
- 22. Вывод полученного выражения
- 23. Творческое задание. Анализ статьи «Inflammation, Aspirin, and the Risk of Cardiovascular Disease in Apparently Healthy Men»
- 24. Что изучалось Увеличивает ли воспалительный процесс риск возникновения тромботических заболеваний; снижает ли приём аспирина этот риск.
- 25. Методика Авторы измерили уровень плазменного C-реактивного белка, маркер системного воспаления, у 543 здоровых мужчин, у которых
- 26. Перед рандомизацией в период с августа 1982 года по декабрь 1984 года потенциальным участникам было предложено
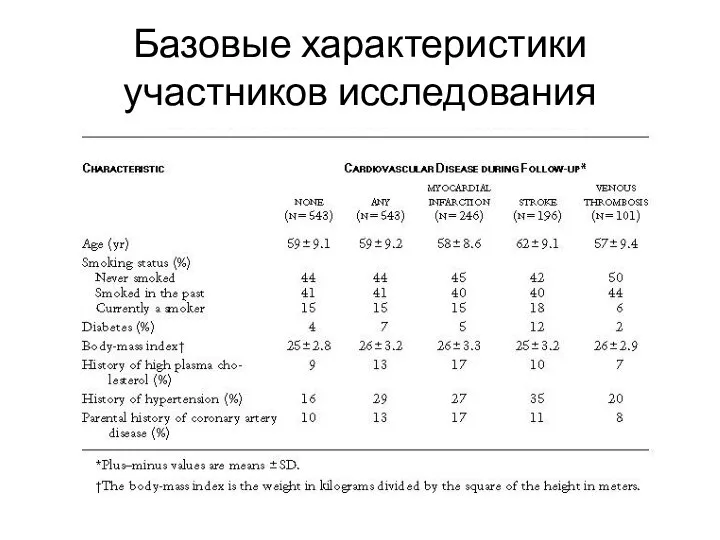
- 27. Базовые характеристики участников исследования
- 28. Статистика Для пациентов из контрольной группы были рассчитаны средние или доли для базовых факторов риска. Значение
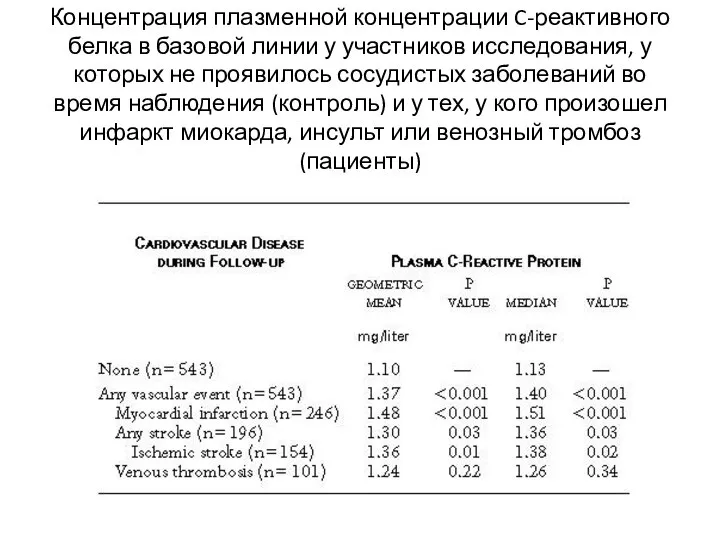
- 29. Концентрация плазменной концентрации C-реактивного белка в базовой линии у участников исследования, у которых не проявилось сосудистых
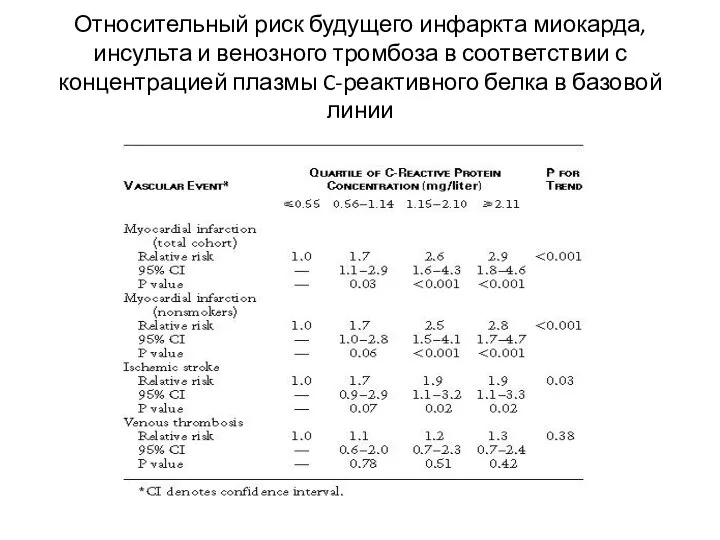
- 30. Относительный риск будущего инфаркта миокарда, инсульта и венозного тромбоза в соответствии с концентрацией плазмы C-реактивного белка
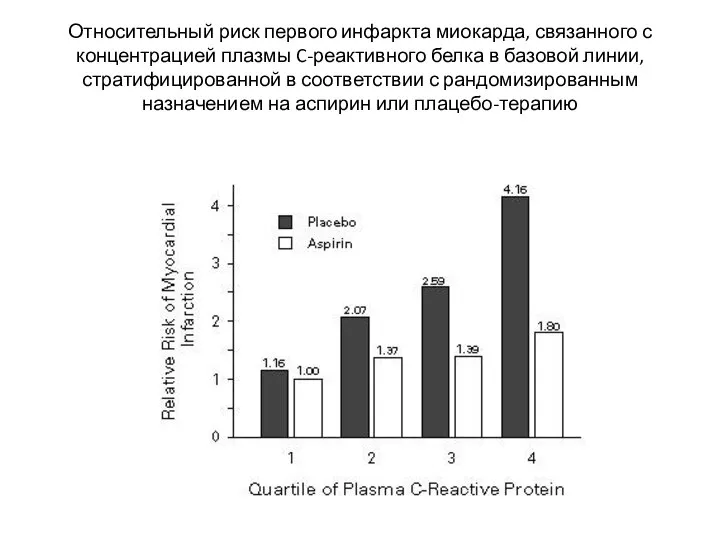
- 31. Относительный риск первого инфаркта миокарда, связанного с концентрацией плазмы C-реактивного белка в базовой линии, стратифицированной в
- 32. Разбор статистической методики U-критерий Манна — Уитни
- 33. Представление данных Выборка 1 (объём n1): x11, x21, …, ; Выборка 2 (объём n2): x12, x22,
- 34. Представление данных Выборка вторая (объём n2) Наблюдение x12, x22, …, Ранг r12, r22, …, Сумма рангов
- 35. Статистическая модель Все наблюдения независимы. Наблюдения, входящих в одну выборку, относятся к одной совокупности.
- 36. Гипотезы Н0: совокупности одинаково распределены; Н1: нулевая гипотеза неверна
- 37. Критериальная статистика Малые выборки Вычисляются и берётся U = max(U1, U2)
- 38. Критериальная статистика Большие выборки В том случае, когда объём меньшей выборки больше 20 или объём большей
- 39. Критериальная статистика В том случае, если совпадающие ранги существуют, то где j — число связок, tj
- 40. Поправка Йейтса Отсутствие поправки на непрерывность приводит к увеличению значения статистики и, соответственно, уменьшению величины достигнутого
- 41. Результаты статьи В статье были сравнены концентрации С-реактивного белка у двух групп мужчин (по 543 человека
- 42. Результаты статьи Экспериментальная концентрации С-реактивного белка в плазме предсказывает риск будущего инфаркта миокарда и инсульта. Более
- 43. Список использованной литературы: Ивашёв-Мусатов О. С. Теория вероятностей и математическая статистика: Учеб. пособие. — 2-е изд.,
- 45. Скачать презентацию





























 Правильные многогранники
Правильные многогранники Разложение многочлена на множители с помощью комбинации различных приемов
Разложение многочлена на множители с помощью комбинации различных приемов ДА, ПУТЬ ПОЗНАНИЯ НЕ ГЛАДОК! НО ЗНАЕМ МЫ СО ШКОЛЬНЫХ ЛЕТ: ЗАГАДОК БОЛЬШЕ, ЧЕМ ОТГАДОК И ПОИСКАМ ПРЕДЕЛА НЕТ!
ДА, ПУТЬ ПОЗНАНИЯ НЕ ГЛАДОК! НО ЗНАЕМ МЫ СО ШКОЛЬНЫХ ЛЕТ: ЗАГАДОК БОЛЬШЕ, ЧЕМ ОТГАДОК И ПОИСКАМ ПРЕДЕЛА НЕТ! Отрезок. Прямая. Луч
Отрезок. Прямая. Луч Измерительные работы на местности
Измерительные работы на местности Прямокутник. Його властивості та ознаки. (8 класс)
Прямокутник. Його властивості та ознаки. (8 класс) О, математики! Игра
О, математики! Игра Треугольник. Самостоятельная работа
Треугольник. Самостоятельная работа Интерактивный тренажёр «Учим таблицу умножения и деления»
Интерактивный тренажёр «Учим таблицу умножения и деления» Решение задач по теме «Признаки параллельности прямых»
Решение задач по теме «Признаки параллельности прямых» Логическое следствие и метод резолюций. (Глава 3)
Логическое следствие и метод резолюций. (Глава 3) Числовые суеверия Презентация Ученицы 6Г класса Лицея №179 Маловой Александры
Числовые суеверия Презентация Ученицы 6Г класса Лицея №179 Маловой Александры  Тест. Геометрические фигуры
Тест. Геометрические фигуры Начальные геометрические сведения
Начальные геометрические сведения Задачі у навчанні математики. Методика навчання учнів розв'язуванню задач
Задачі у навчанні математики. Методика навчання учнів розв'язуванню задач Правильные многоугольники
Правильные многоугольники Случайные события и вероятность
Случайные события и вероятность Математические и инструментальные методы поддержки принятия решений
Математические и инструментальные методы поддержки принятия решений Полет – это математика
Полет – это математика Степенная функция. 10 класс
Степенная функция. 10 класс Аппроксимация функций. Метод Лагранжа
Аппроксимация функций. Метод Лагранжа Теорія двоїстості та аналіз лінійних оптимізаційних задач
Теорія двоїстості та аналіз лінійних оптимізаційних задач Сумма углов треугольника (метод ножниц)
Сумма углов треугольника (метод ножниц) Дискретне перетворення Фур’є
Дискретне перетворення Фур’є Задачи на работу и производительность труда работников железнодорожной станции Батайск
Задачи на работу и производительность труда работников железнодорожной станции Батайск Урок-квн Правила дифференцирования
Урок-квн Правила дифференцирования Аттестационная работа. Решение уравнений и задач в целых числах
Аттестационная работа. Решение уравнений и задач в целых числах Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии
Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии