Содержание
- 2. Темы лекции Нелинейная регрессия Преобразования переменных Экономическая интерпретация регрессионной модели
- 3. Направления анализа и развития парной линейной регрессии Ключевые точки (начало координат) Кривая или прямая Форма криволинейной
- 4. Этапы построения модели 1. Выбор теоретических предпосылок 2. Формализация предпосылок 3. Построение математической модели 4. Анализ
- 5. Производственная функция Кобба-Дугласа Многие экономические процессы не являются линейными по сути. Их моделирование линейными уравнениями не
- 6. Классы нелинейных регрессий Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно переменных, но линейные по
- 7. Классы нелинейных регрессий Линейная модель Модель, нелинейная по переменным После подстановки модель стала линейной Модель, нелинейная
- 8. Линейная модель
- 9. Линейная модель Если переменная X увеличится на 1, то Y изменится в среднем на β единиц
- 10. Моделирование эластичности Независимо от вида математической связи между Y и X эластичность равна: Эластичность y по
- 11. Пример расчета эластичности Рассмотрим кривую Энгеля: где Y – спрос на товар, X – доход. Имеем:
- 12. Эластичность – переменная величина Например, для линейной модели Эластичность не всегда бывает постоянной для различных значений
- 13. Средний коэффициент эластичности Средний коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат
- 14. Логарифмическая форма Прологарифмировав обе части уравнения, получим
- 15. Логарифмическая форма Интерпретация коэффициента регрессии β – эластичность зависимой переменной по объясняющей переменной Коэффициент при объясняющей
- 16. Логарифмическая форма Вычисление наклона (скорости роста) Наклон постоянно меняется с изменением номера наблюдения
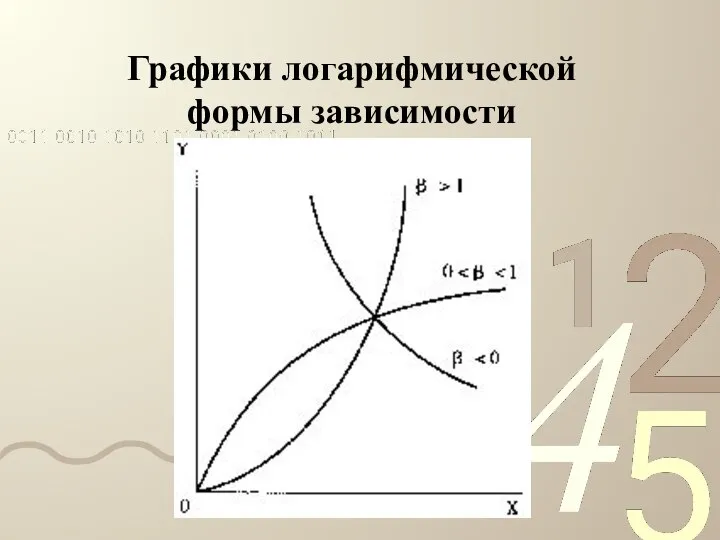
- 17. Графики логарифмической формы зависимости
- 18. Логарифмически-линейная форма Интерпретация коэффициента регрессии β: Коэффициент при объясняющей переменной показывает на сколько процентов возрастает Y
- 19. Логарифмически-линейная форма Эластичность растет с ростом Y: Это указывает на класс зависимостей, где следует применять линейно-логарифмическую
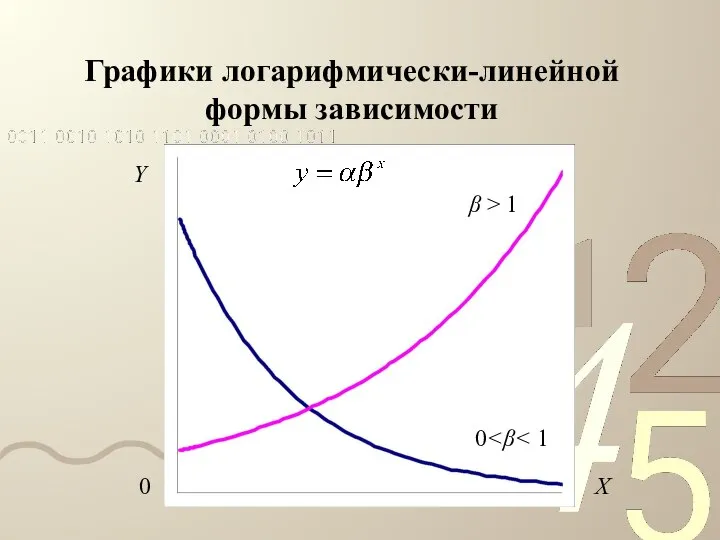
- 20. Графики логарифмически-линейной формы зависимости Y β > 1 0 X 0
- 21. Логарифмически-линейная форма от времени Вид уравнения: Интерпретация: Коэффициент при переменной времени выражает темп прироста. Он показывает
- 22. Преобразование случайного отклонения Пример. Логарифмирование нелинейной модели с аддитивным случайным членом не приводит к линеаризации соотношения
- 23. Сравнение различных моделей 1. Содержательный анализ 2. Формальный анализ: Метод Зарембки Преобразование Бокса-Кокса
- 24. Метод Зарембки Применим для выбора из двух форм (несравнимых непосредственно), в одной из которых зависимая переменная
- 25. Сравнение различных моделей парной регрессии методом Зарембки 1. Вычисляем среднее геометрическое значений зависимой переменной и все
- 26. Сравнение различных моделей парной регрессии методом Зарембки 3. Вычисляем χ2-статистику для оценки значимости различий 4. Сравниваем
- 27. Метод Бокса-Кокса Идея метода. Переменная : при λ=1 превращается в линейную функцию при λ→0 переходит в
- 28. Сравнение различных моделей парной регрессии методом Бокса-Кокса 1. Преобразуют зависимую переменную по методу Зарембки: 2. Рассчитывают
- 29. Сравнение различных моделей парной регрессии методом Бокса-Кокса 3. Рассчитывают уравнения регрессии для новых переменных при значениях
- 31. Скачать презентацию


























 Аттестационная работа. Доли. Обыкновенные дроби. (5 класс)
Аттестационная работа. Доли. Обыкновенные дроби. (5 класс) Формулы сокращенного умножения. Путешествие «По стране формул»
Формулы сокращенного умножения. Путешествие «По стране формул» Подготовка к контрольной работе по алгебре. 8 класс
Подготовка к контрольной работе по алгебре. 8 класс Принципы решения слабоструктурированных проблем
Принципы решения слабоструктурированных проблем Презентация по математике "Как математику преподавать, чтоб математиками стать" - скачать
Презентация по математике "Как математику преподавать, чтоб математиками стать" - скачать  Работа с функциями в Open Office Calc
Работа с функциями в Open Office Calc Тиждень математики “Цариці всіх наук присвячується”
Тиждень математики “Цариці всіх наук присвячується” Физико-математический КВН в 9-х классах
Физико-математический КВН в 9-х классах Подготовка к ЕГЭ по математике. Решение задач В5
Подготовка к ЕГЭ по математике. Решение задач В5 Занимательная геометрия
Занимательная геометрия Геометрическая вероятность
Геометрическая вероятность Матдрака 2011. Математический фестиваль
Матдрака 2011. Математический фестиваль Козлова Галина Алексеевна 218 – 152 – 392 Урок по математике 4 класс Тема урока: Умножение многозначного числа на трехзн
Козлова Галина Алексеевна 218 – 152 – 392 Урок по математике 4 класс Тема урока: Умножение многозначного числа на трехзн Тест по теме: "Прямоугольный параллелепипед". Часть 1
Тест по теме: "Прямоугольный параллелепипед". Часть 1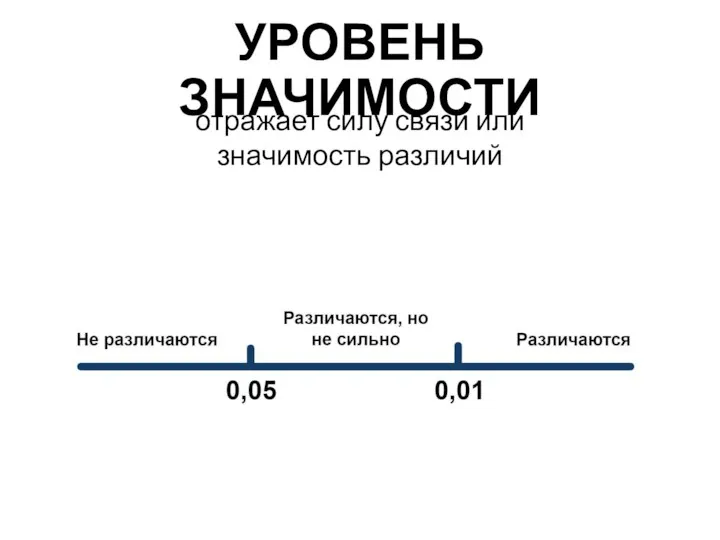 Уровень значимости
Уровень значимости Объем пирамиды
Объем пирамиды Обработка многократно измеренных величин
Обработка многократно измеренных величин Точка. Линии прямые и кривые. Отрезок. Луч
Точка. Линии прямые и кривые. Отрезок. Луч Презентация на тему Многоугольник. Четырехугольник.
Презентация на тему Многоугольник. Четырехугольник. Быстрый счёт
Быстрый счёт Область определения и область значения показательной, логарифмической и степенной функций Учителя математики МОУ СОШ № 73 Антипо
Область определения и область значения показательной, логарифмической и степенной функций Учителя математики МОУ СОШ № 73 Антипо Симметрия в пространстве
Симметрия в пространстве Площадь трапеции. Задачи
Площадь трапеции. Задачи Общие методы решения тригонометрических уравнений
Общие методы решения тригонометрических уравнений Аттестационная работа. Методическая разработка по выполнению проекта В стране задач
Аттестационная работа. Методическая разработка по выполнению проекта В стране задач Задачи на готовых чертежах
Задачи на готовых чертежах Теорема о сложении вероятностей
Теорема о сложении вероятностей Одночлен и его стандартный вид
Одночлен и его стандартный вид