Содержание
- 2. Основные определения теории проверки гипотез Определение: Статистическим критерием (тестом) называется правило, позволяющее на основании наблюдений принять
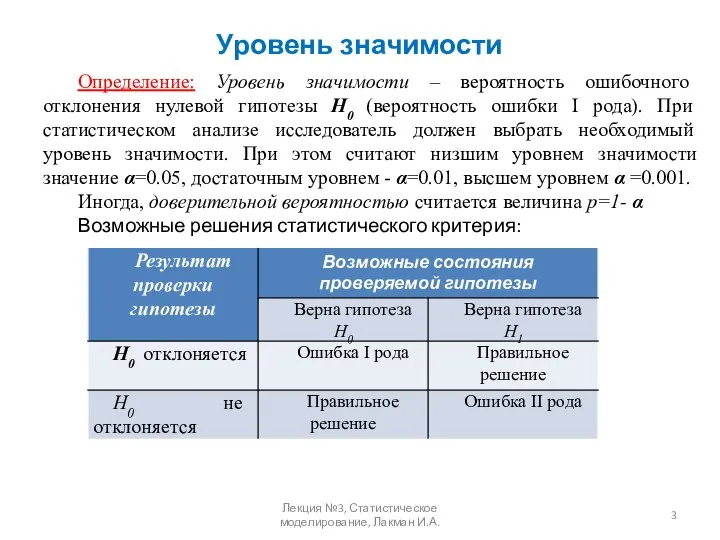
- 3. Уровень значимости Определение: Уровень значимости – вероятность ошибочного отклонения нулевой гипотезы Н0 (вероятность ошибки I рода).
- 4. Ошибки I и II рода Определение 1: В процессе проверки гипотезы существует вероятность того, что Н0
- 5. Этапы принятия статистического решения Формулировка нулевой и альтернативной гипотез. Определение объема выборки. Выбор соответствующего уровня значимости
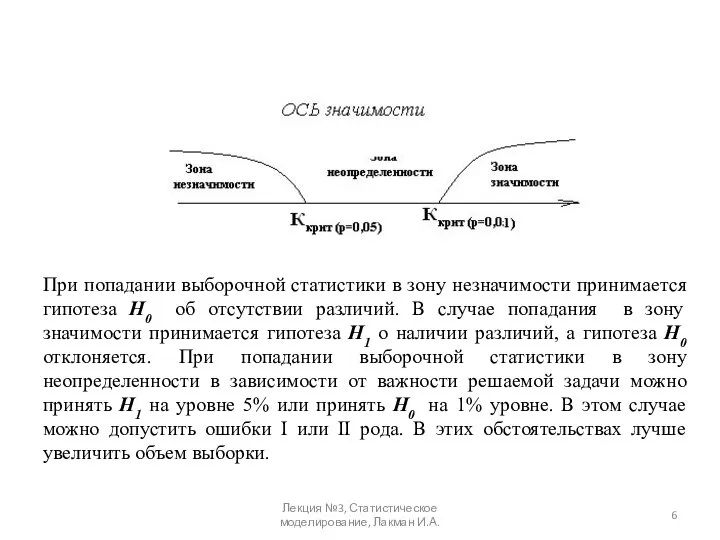
- 6. При попадании выборочной статистики в зону незначимости принимается гипотеза Н0 об отсутствии различий. В случае попадания
- 7. Проверка гипотезы о соответствии исправленной выборочной дисперсии величине генеральной дисперсии нормальной совокупности Стандартизированный статистический критерий (тест)
- 8. Проверка гипотезы о соответствии исправленной выборочной дисперсии величине генеральной дисперсии нормальной совокупности Правосторонняя проверка: нулевая и
- 9. Проверка гипотезы о соответствии выборочной средней величине генеральной средней нормальной совокупности Формируем гипотезы о равенстве генеральной
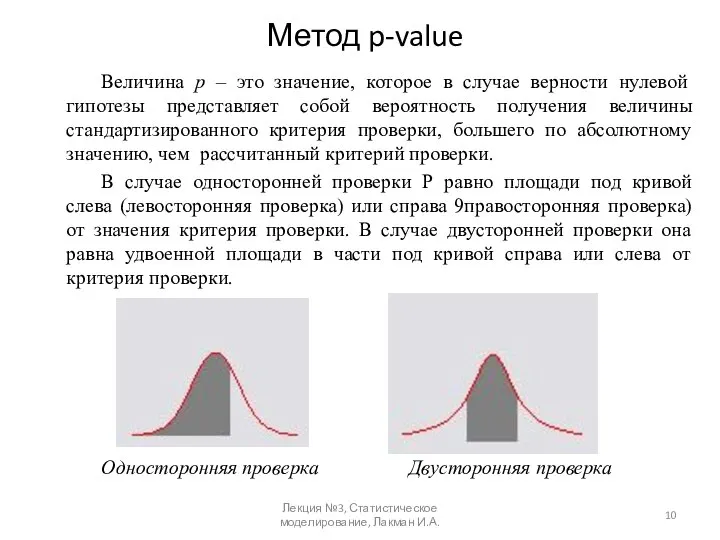
- 10. Метод p-value Величина р – это значение, которое в случае верности нулевой гипотезы представляет собой вероятность
- 11. Метод p-value В методе p-value правило принятия решения одинаково независимо то того, выполняется левосторонняя, правосторонняя или
- 12. Задача оценивания Пусть имеются данные выборки, например значения некоторого признака, Х1, Х2,…, Хn, полученные в результате
- 13. Свойства оценок Полученные оценки должны быть достоверными, т.е. обладать свойствами несмещенности, эффективности и состоятельности. Несмешанной называют
- 14. Метод моментов для точечной оценки параметра распределения Оценка одного параметра Вид плотности распределения f(x, θ). Требуется
- 15. Метод моментов для точечной оценки параметра распределения Оценка двух параметров Вид плотности распределения f(x, θ1, θ2).
- 16. Метод максимального правдоподобия Для дискретных случайных величин. Пусть Х дискретная случайная величина, которая принимает возможные значения
- 17. Метод максимального правдоподобия Определение: Оценкой максимального правдоподобия называют такую оценку , для которой функция правдоподобия достигает
- 18. Метод максимального правдоподобия Для непрерывных случайных величин. Пусть Х непрерывная случайная величина, которая пв результате испытания
- 19. Метод максимального правдоподобия Для непрерывных случайных величин. Если плотность распределения f(x) непрерывной случайной величины Х определяется
- 20. Статистическая задача оценивания Задача: по наблюдениям х1, х2,…,хп над случайной величиной Х, распределенной равномерно на отрезке
- 21. Теоретическое сравнение оценок Все оценки являются несмещенными, их математические ожидания равны истинным параметрам а. (доказать сам-но)
- 22. Статистическое сравнение оценок Значение оценок концентрируются в окрестности оцениваемого параметра (свойство несмещенности). С ростом числа наблюдений
- 24. Скачать презентацию


















 Математика. Информатика. Физика. Игра-виктрина
Математика. Информатика. Физика. Игра-виктрина “Математика – царица наук, арифметика – царица математики”
“Математика – царица наук, арифметика – царица математики” Приближённые методы вычисления определённых интегралов
Приближённые методы вычисления определённых интегралов Актуализация знаний
Актуализация знаний Тригонометрическая окружность. Тригонометрические функции
Тригонометрическая окружность. Тригонометрические функции Көпбұрыштың ортогональ проекциясының ауданы
Көпбұрыштың ортогональ проекциясының ауданы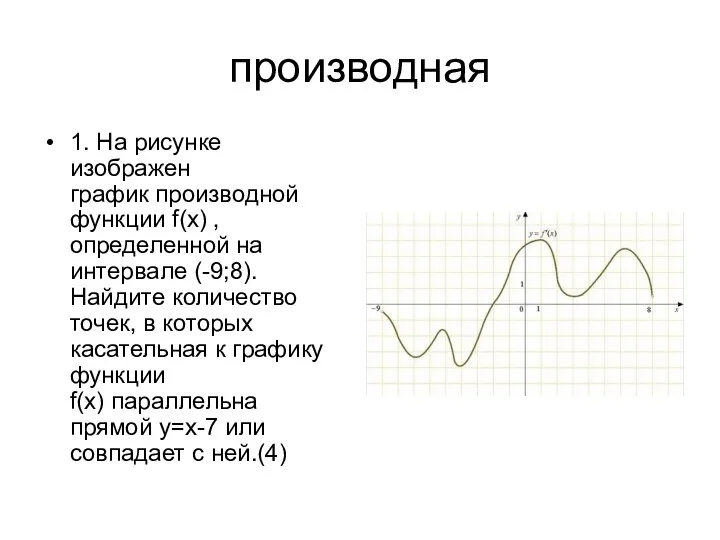 Производная. График производной функции
Производная. График производной функции Пространство и время. Всеобщие формы существования материи
Пространство и время. Всеобщие формы существования материи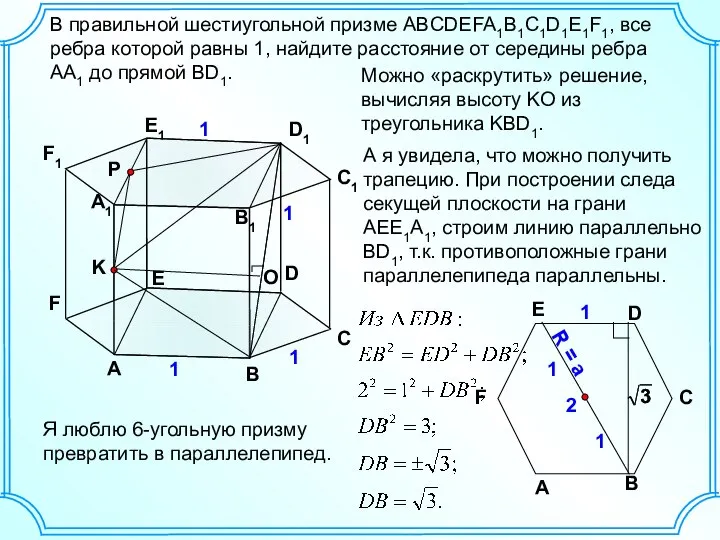 Решение задач
Решение задач Множества и операции над ними
Множества и операции над ними Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Плоскость и прямая в пространстве
Плоскость и прямая в пространстве Таблица умножения и деления на 5
Таблица умножения и деления на 5 Арккосинус и решение уравнения cost=а
Арккосинус и решение уравнения cost=а Случайные величины и функции распределения (лекция 1)
Случайные величины и функции распределения (лекция 1) Число и цифра 7. Урок №49. 1 класс.2 четверть. Учитель начальных классов: Андреева Елена Петровна Школа №3 г.Нытва
Число и цифра 7. Урок №49. 1 класс.2 четверть. Учитель начальных классов: Андреева Елена Петровна Школа №3 г.Нытва Тема 5. Вступ до математичного аналізу. Лекція №11. Неперервність функції. Визначні границі
Тема 5. Вступ до математичного аналізу. Лекція №11. Неперервність функції. Визначні границі Параллельный перенос
Параллельный перенос Презентация по математике "Число 8" - скачать бесплатно
Презентация по математике "Число 8" - скачать бесплатно Статистические методы прогнозирования
Статистические методы прогнозирования Алғашқы функция және интеграл
Алғашқы функция және интеграл Неравенства. Метод замены множителей
Неравенства. Метод замены множителей Решение уравнений. Задачи на составление уравнений
Решение уравнений. Задачи на составление уравнений Расстояние от точки до фигуры
Расстояние от точки до фигуры Аттестационная работа. Методическая разработка по выполнению проекта по математике Некоторые замечательные кривые
Аттестационная работа. Методическая разработка по выполнению проекта по математике Некоторые замечательные кривые В поисках затонувшего клада
В поисках затонувшего клада Подготовка к ГИА по математике. Задания 8
Подготовка к ГИА по математике. Задания 8 Прямоугольный треугольник
Прямоугольный треугольник