Содержание
- 2. «Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад»
- 3. Применение производной при исследовании функции Промежутки возрастания и убывания функции
- 4. 1. Если f ′(x) › 0в каждой точке интервала I, то функция f(x) возрастает на I.
- 5. 1. Найдите область определения функции. 2. Найдите производную функции. 3. Найдите точки, в которых производная равна
- 6. Определите промежутки возрастания, убывания функции: f (x) = 3x - x³ D(f) = (-∞;∞) f ′(x)
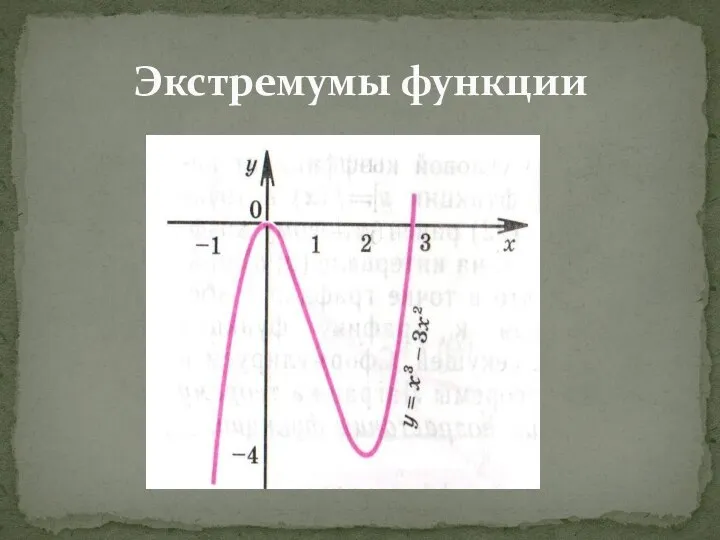
- 10. Экстремумы функции
- 11. Точка х₀ называется точкой максимума функции f(x), если существует такая окрестность точки х₀ , что для
- 12. Точка х₀ называется точкой минимума функции f(x), если существует такая окрестность точки х₀ , что для
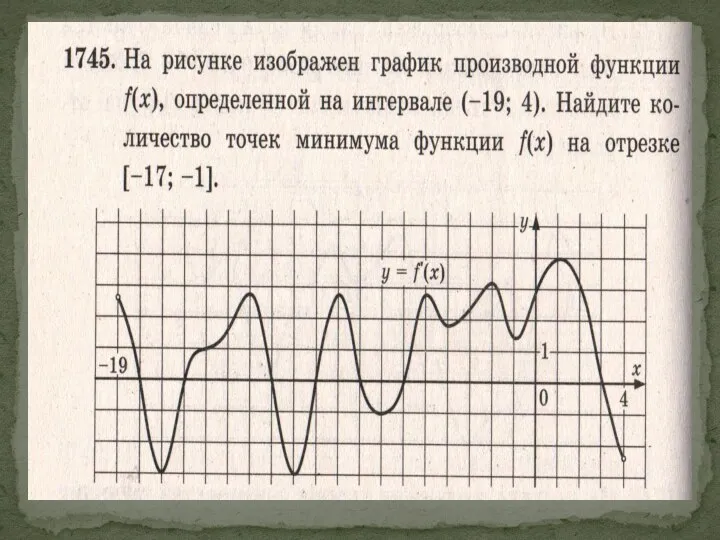
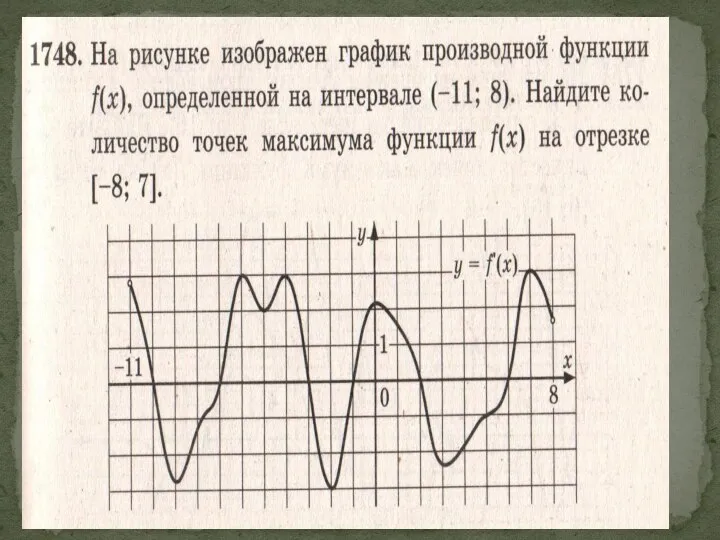
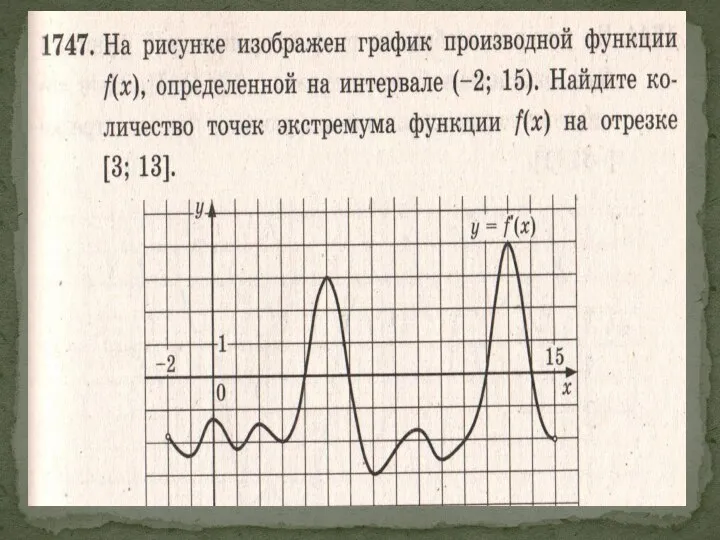
- 13. Экстремумами функции Точки максимума и минимума функции называются
- 15. Ответ 3
- 16. 1. Найдите область определения функции. 2. Найдите производную функции. 3. Найдите точки, в которых производная равна
- 19. Наибольшее и наименьшее значение функции
- 20. 1. Найдите производную функции. 2. Найдите критические точки функции. 3.Найдите значения функции на концах отрезка [a;b]
- 21. Образцы решения
- 22. 1. f (x) = 1 + 8x – x² [2; 5] 2. f (x) = 3x²
- 24. Схема исследования функции: 1. Найдите область определения функции. 2. Найдите производную функции. 3. Найдите критические точки
- 25. Исследуйте функцию и постройте график: f(x) = 3x² - x³ 1. D(f) = (-∞; ∞) 2.
- 28. Скачать презентацию
















![1. f (x) = 1 + 8x – x² [2; 5]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/696750/slide-21.jpg)




 Sequential games. Empirical evidence and bargaining. (Lecture 5)
Sequential games. Empirical evidence and bargaining. (Lecture 5) Решение задач. Треугольники, часть 2
Решение задач. Треугольники, часть 2 Призма
Призма Проверка статистических гипотез
Проверка статистических гипотез Объём и поверхность тел вращения. Вычисление комфортности жилища
Объём и поверхность тел вращения. Вычисление комфортности жилища Серия СМОГ-У. Прямоугольник, ромб, квадрат
Серия СМОГ-У. Прямоугольник, ромб, квадрат Методы решений заданий С5 (задачи с параметром)
Методы решений заданий С5 (задачи с параметром)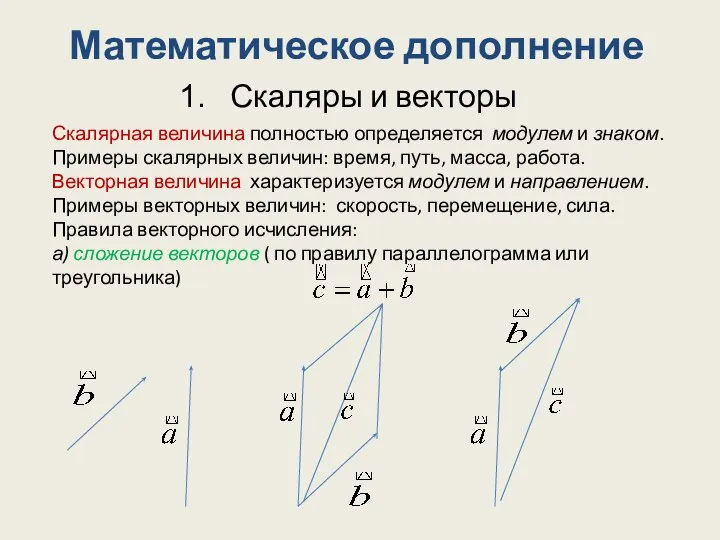 Математическое дополнение
Математическое дополнение Аксиомы стереометрии
Аксиомы стереометрии Общие принципы проверки статистических гипотез. (Лекция 2)
Общие принципы проверки статистических гипотез. (Лекция 2) Применение нестандартных форм и методов обучения в 5 -6 классах
Применение нестандартных форм и методов обучения в 5 -6 классах Координаты
Координаты Натуральные числа и шкалы
Натуральные числа и шкалы Преобразование алгебраических выражений
Преобразование алгебраических выражений Статистические методы прогнозирования
Статистические методы прогнозирования Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ
Элементы комбинаторики, статистики и теории вероятностей. Решение заданий В 10 ЕГЭ Двойной интеграл
Двойной интеграл Виды треугольников
Виды треугольников Cálculo numérico. Integração Numérica. (Aula 8)
Cálculo numérico. Integração Numérica. (Aula 8) Отношения и отображения
Отношения и отображения Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков
Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков Випадкові похибки непрямих вимірювань
Випадкові похибки непрямих вимірювань Числовые неравенства
Числовые неравенства Операции импликация, эквивалентность. Примеры законов алгебры логики. Эквивалентные преобразования логических выражений
Операции импликация, эквивалентность. Примеры законов алгебры логики. Эквивалентные преобразования логических выражений Теория вероятностей. Определение вероятности случайного события. Элементы комбинаторики
Теория вероятностей. Определение вероятности случайного события. Элементы комбинаторики Таинственные острова математики
Таинственные острова математики Измерения физических величин
Измерения физических величин Случаи сложения …+2 . …+3
Случаи сложения …+2 . …+3