Содержание
- 2. Испытания и исходы Испытанием назовем эмпирические наблюдения, тестирование, проведение эксперимента. Пример испытания: подбрасывание игральной кости. В
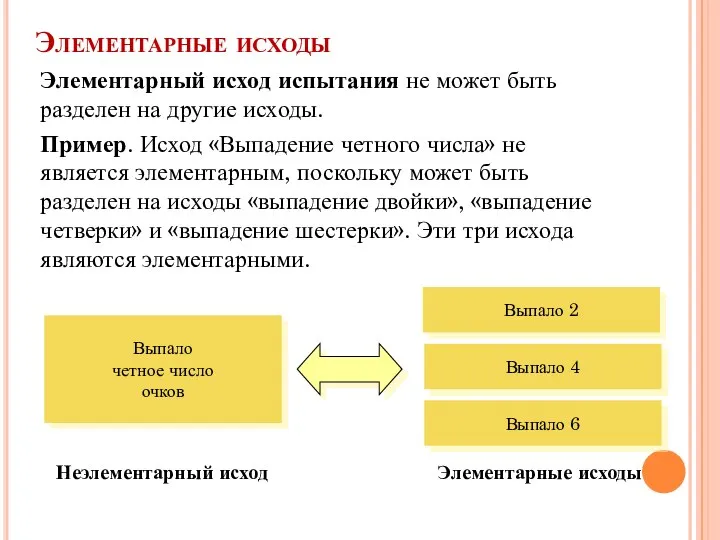
- 3. Элементарные исходы Элементарный исход испытания не может быть разделен на другие исходы. Пример. Исход «Выпадение четного
- 4. Пространство элементарных исходов Пространство элементарных исходов включает все элементарные исходы, которые могут произойти в результате испытания.
- 5. Диаграмма Венна Для графического представления пространства случайных событий и отношений между событиями принято использовать диаграммы Венна
- 6. Случайное событие Пространство элементарных исходов Событие А Случайное событие есть некоторое подмножество пространства элементарных исходов испытания.
- 7. Примеры случайных событий Случайное событие – некоторое подмножество пространства элементарных исходов испытания.
- 8. Невозможное и достоверное события Достоверным назовем событие, наступающее при любом исходе испытания. Невозможным назовем событие, не
- 9. Равновозможные события Равновозможными назовем события, для которых есть основания считать, что ни одно из них не
- 10. Несовместные события Событие А Событие B События А и В называются несовместными, если они не могут
- 11. Примеры совместные события идет дождь и идет снег; человек ест и человек читает; число целое и
- 12. Противоположное событие (по отношению к рассматриваемому событию А) это событие , которое не происходит, если А
- 13. Примеры если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он
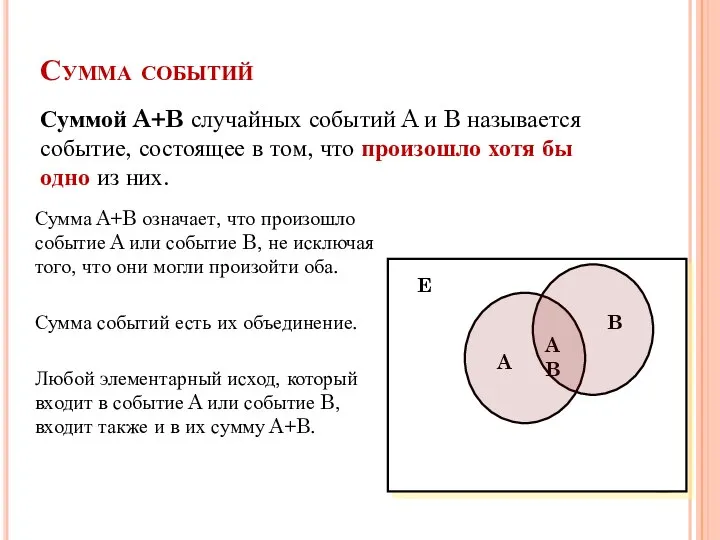
- 14. Сумма событий Суммой A+B случайных событий A и B называется событие, состоящее в том, что произошло
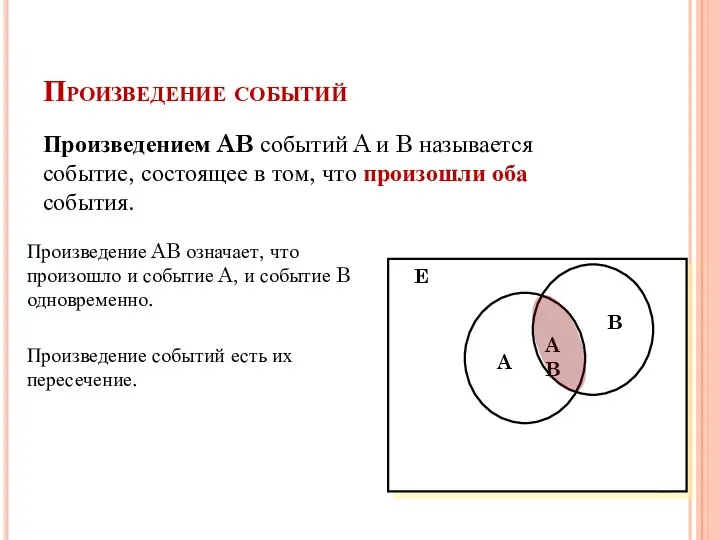
- 15. Произведение событий Произведением AB событий A и B называется событие, состоящее в том, что произошли оба
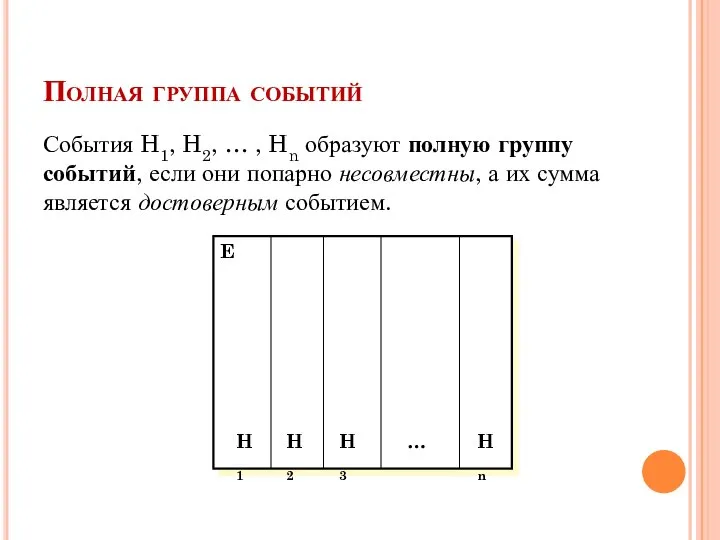
- 16. Полная группа событий H1 E H2 Hn H3 … События H1, H2, … , Hn образуют
- 17. Благоприятные исходы Элементарные исходы, образующие событие А, назовем благоприятными. Если мы ожидаем событие А, то появление
- 18. 15 февраля 2015 г. Классическое определение вероятности
- 19. Пьер-Симо́н Лапла́с Классическое определение вероятности было впервые дано в работах французского математика Лапласа.
- 20. Вероятностью события А назовем отношение числа благоприятных исходов к общему числу элементарных исходов: где m –
- 21. Свойства вероятности Свойство 1. Вероятность достоверного события равна единице. Свойство 2. Вероятность невозможного события равна нулю.
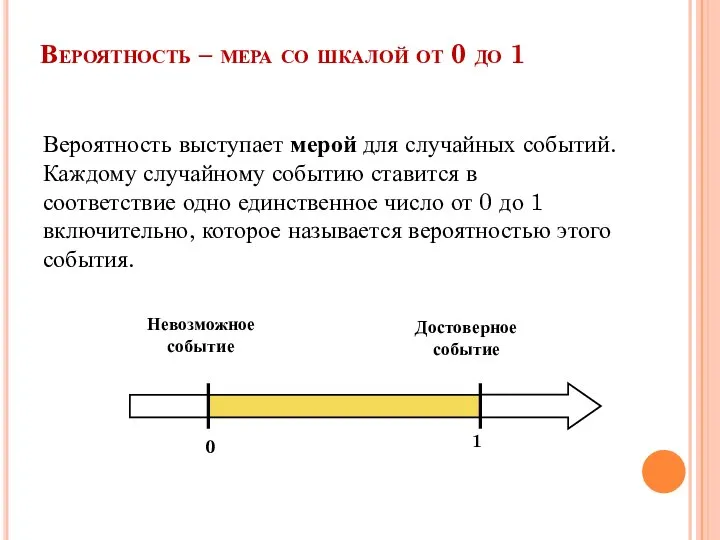
- 22. Вероятность – мера со шкалой от 0 до 1 0 1 Невозможное событие Достоверное событие Вероятность
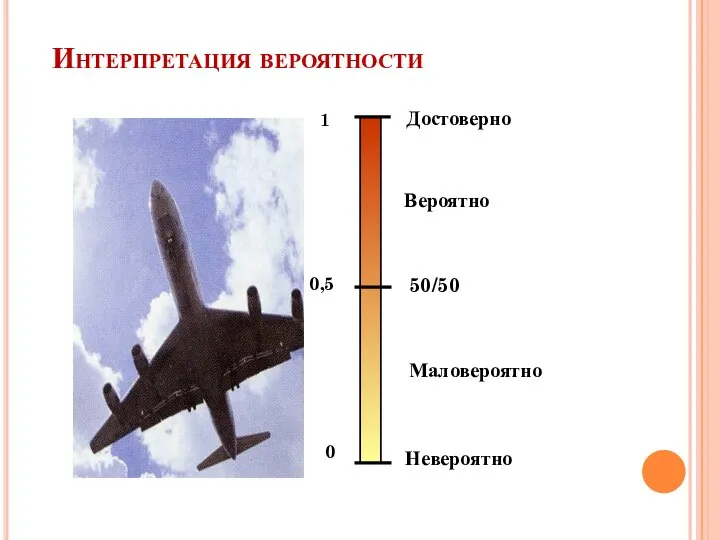
- 23. Интерпретация вероятности 0 1 Невероятно Достоверно 0,5 50/50 Маловероятно Вероятно
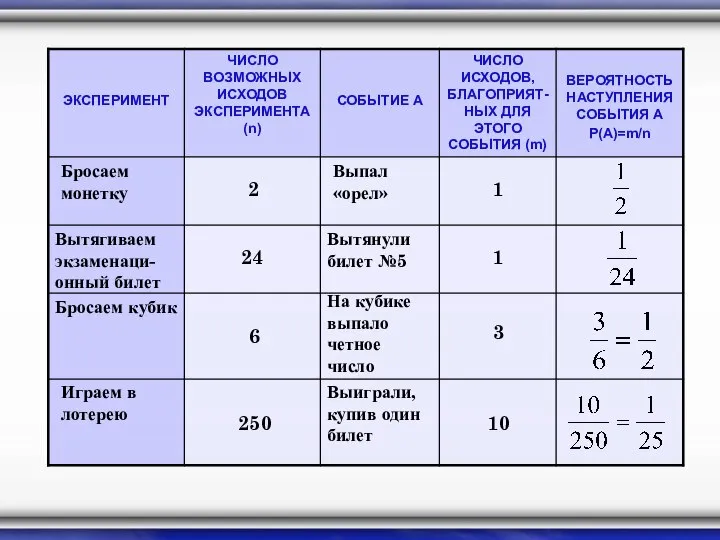
- 24. Бросаем монетку 2 Выпал «орел» 1 Вытягиваем экзаменаци- онный билет Вытянули билет №5 24 1 Бросаем
- 25. Пример. Подбрасываем две монеты. Имеется четыре элементарных исхода: Орел - Орел Орел - Решка Решка -
- 26. Пример. Бросается игральная кость. Элементарные исходы: число выпавших очков равно 1, 2, 3, 4, 5 или
- 27. Правило округления Если вероятность вычисляется в десятичных знаках, округляем ее до трех знаков после запятой: P(A)
- 28. Статистическое определение вероятности
- 29. Ошибка Даламбера Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой
- 30. Ошибка Даламбера Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту
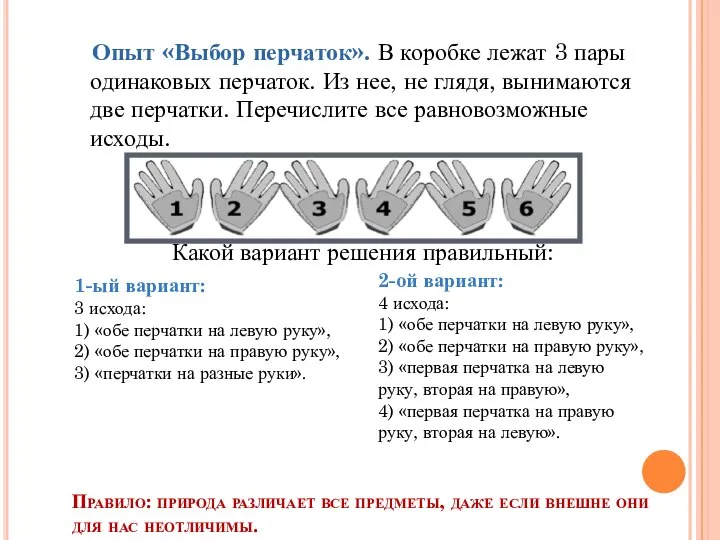
- 31. Опыт «Выбор перчаток». В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две
- 32. Вывод Формула классической вероятности дает очень простой способ вычисления вероятностей. Однако простота этой формулы обманчива. При
- 33. Опыт человечества: Вероятность попасть под дождь в Лондоне гораздо выше, чем в пустыне Сахара. Весь наш
- 34. Частота случайного события Абсолютной частотой случайного события А в серии из N случайных опытов называется число
- 35. Частота случайного события Относительной частотой случайного события называют отношение числа появлений этого события к общему числу
- 36. Примеры Пример 1. Наблюдения показывают, что в среднем среди 1000 новорожденных детей 515 мальчиков. Какова частота
- 37. Пример 2. За лето на Черноморском побережье было 67 солнечных дней. Какова частота солнечных дней на
- 38. Фундаментальным свойством относительных частот является тот факт, что с увеличением числа опытов относительная частота случайного события
- 39. Пример. Подбрасывание монеты. А – выпадает герб. Классическая вероятность: всего 2 исхода, 1 исход события А:
- 40. Проверка Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб выпал в
- 41. Проверка Английский математик Карл Пирсон (1857-1936) бросал монету 24000 раз, причем герб выпал 12012 раз. Следовательно,
- 42. Результаты Вывод Пример подтверждает естественное предположение о том, что вероятность выпадения герба при одном бросании монеты
- 43. Статистическая вероятность Вероятность случайного события приближенно равна частоте этого события, полученной при проведении большого числа случайных
- 44. Задача №1. Чтобы определить, как часто встречаются в лесопарке деревья разных пород, были проведены следующие эксперименты.
- 45. Решение: а) A={выбранное наугад в парке дерево - сосна} NА = 315, N = 757, Р(А)
- 46. Геометрическая вероятность
- 47. Опыт 1. Выберем на географической карте мира случайную точку (например, зажмурим глаза и покажем указкой). Какова
- 48. ГИПОТЕЗА: Очевидно, для ответа на вопрос нужно знать, какую часть всей карты занимает Россия. Точнее, какую
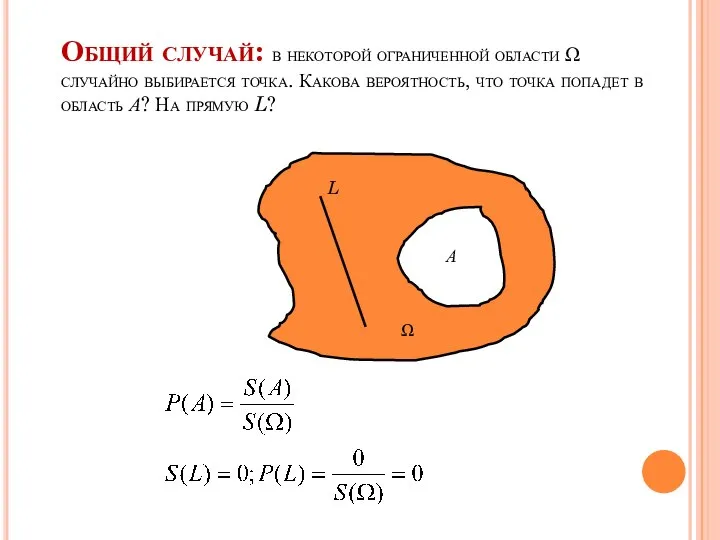
- 49. Общий случай: в некоторой ограниченной области Ω случайно выбирается точка. Какова вероятность, что точка попадет в
- 50. Геометрическое определение вероятности Если предположить, что попадание в любую точку области Ω равновозможно, то вероятность попадания
- 52. Скачать презентацию








































 Условия параллельности и перпендикулярности прямых
Условия параллельности и перпендикулярности прямых Презентация на тему Табличное умножение и деление
Презентация на тему Табличное умножение и деление  Тела гладкие. Тела складчатые
Тела гладкие. Тела складчатые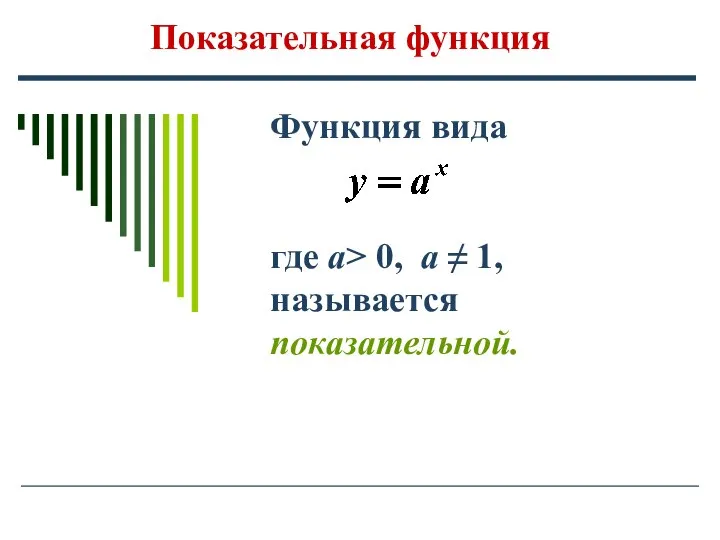 Показательная функция
Показательная функция Способы задания положения тела. Координатная прямая
Способы задания положения тела. Координатная прямая Многогранники
Многогранники Математика 6 класс Колесова Жанна Валерьевна учитель математики МОУ «СОШ п. Бурасы Новобурасского района Саратовской обл
Математика 6 класс Колесова Жанна Валерьевна учитель математики МОУ «СОШ п. Бурасы Новобурасского района Саратовской обл Линейная алгебра
Линейная алгебра Ладанова И.В. МКОУ «Верх-Жилинская ООШ»
Ладанова И.В. МКОУ «Верх-Жилинская ООШ»  Анализ геометрической формы. Порядок чтения чертежей деталей
Анализ геометрической формы. Порядок чтения чертежей деталей Бесконечные периодические десятичные дроби
Бесконечные периодические десятичные дроби Лекция 1. Исследование функции
Лекция 1. Исследование функции Теорема Виета. (8 класс)
Теорема Виета. (8 класс) Игра на поиск логических пар
Игра на поиск логических пар Презентация по математике "Линейная функция и её график" - скачать
Презентация по математике "Линейная функция и её график" - скачать  Приближенные значения чисел. Округление чисел
Приближенные значения чисел. Округление чисел Типовые классы детерминированных аналитических моделей
Типовые классы детерминированных аналитических моделей Смежные углы
Смежные углы Математический диктант
Математический диктант Неравенство треугольника
Неравенство треугольника Решение показательных уравнений. 10 класс
Решение показательных уравнений. 10 класс Презентация по математике "Равные фигуры" - скачать
Презентация по математике "Равные фигуры" - скачать  Масштаб
Масштаб Модуль числа. Урок математики в 6 классе
Модуль числа. Урок математики в 6 классе Математическая викторина
Математическая викторина Кубический корень
Кубический корень Маршрутный лист группы
Маршрутный лист группы Космические задачи. Подготовка к ЕГЭ и ГИА
Космические задачи. Подготовка к ЕГЭ и ГИА